
Mathematics is sometimes seen as a separate world altogether from the humanities. Questions from the humanities have gray areas and room for debate, whereas math is a cold crystal ball that deems answers “right” or “wrong” and has students memorizing convoluted methods to learn its ways.
But math has gray areas! Consider these questions:
- If there are three candidates running for office, how should voters choose a winner?
- What is 8 ÷ 2(2 + 2)?
- If you earn $50,000 per year and pay $1,000 per month in rent, what is the best strategy for saving money?
Let's dig into each of these.
1. If there are three candidates running for office, how should voters choose a winner?
This one seems so straightforward, right? Everyone votes for a winner, and whoever gets the most votes win. This is, of course, not how all US government candidates are elected. Moreover, the idea is fraught with mathematical paradox. To see why, let's imagine there are exactly 100 voters and three candidates: Alex, Betty, and Carlos. Consider two voting scenarios.
- SCENARIO A: Everyone votes for one person. Alex gets 40 votes, and Betty and Carlos get 30 votes each.
- SCENARIO B: Everyone votes for two people and numbers them 1 and 2 for first and second choice. Just like Scenario A, 40 people put '1' for Alex, 30 people put '1' for Betty, and 30 people put '1' for Carlos. But then EVERYONE who votes '1' for Alex or Carlos votes '2' for Betty. (The people who vote '1' for Betty are split between Alex and Carlos.)
Is it fair that in Scenario A, Alex wins, but if you include the first- and second-place votes in Scenario B, Betty would be overall more popular? As much as we want voting to be perfectly fair, by changing the voting process, the exact same people end up electing different candidates. (Classroom activity: task students with deciding how to vote and have them compare the pros and cons of each other's methods.)
2. What is 8 ÷ 2(2 + 2)?
This math problem has gone viral before. It seems so clear-cut! The challenge is that people either forget or misuse the standard order of operations, which requires evaluating parentheses first, followed by multiplication and division in order from left to right. Thus the “correct” answer of 16 (which is 8 ÷ 2 • 4) is obscured by the sloppy notation.
However, order of operations is something learned, not immutable mathematical law. The proper order of operations has evolved throughout history and varies geographically. Students and mathematicians alike ignore it sometimes and with good reason, for example by leaving out parentheses when they're implied or writing an expression as it would be entered into a four-operation calculator. (Classroom activity: ask students to invent their own algorithms for evaluating expressions and explore how those algorithms would affect specific formulas.)
3. If you earn $50,000 per year and pay $1,000 per month in rent, what is the best strategy for saving money?
Here, math flirts closely with the humanities. Figuring out a strategy for saving money absolutely involves mathematics, and the more details one considers, the more sophisticated it can get.
- How long are you trying to save for?
- What are your other expenses?
- How will inflation affect the amount you have saved?
Yet exploring the question fully requires asking questions whose answers are not strictly mathematical.
- What is your personal risk tolerance?
- How compulsively do you spend?
- How were you taught about money growing up?
Despite what many students (and plenty of adults, too) may think, math problems rarely have a single method for solving them and frequently have multiple solutions. Students should be encouraged to explore new ways to solve the same problems.
Let’s take a look at a straightforward math problem that will look familiar to any fourth grader:
Divide 272 by 4.
Every fourth grade curriculum shows at least one strategy for solving it. Let's explore a few.
Strategy 1: Visual Representation
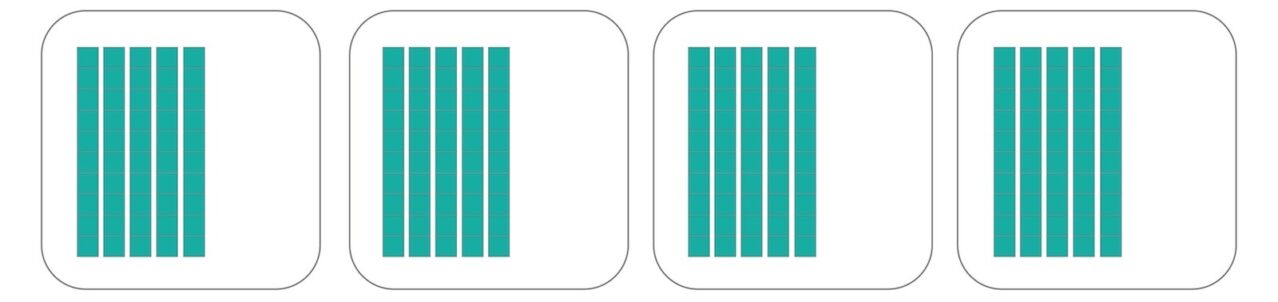
This strategy is an excellent tool to get students acquainted with the idea of division, although it does not generalize well when the dividend or divisor is large or complicated. Because the goal is to divide a number (272) into 4 equal parts, create 4 buckets for the parts to go in.
Now fill in the sections evenly. A student might start by putting 50 units in each section, getting them to close with 200 total.
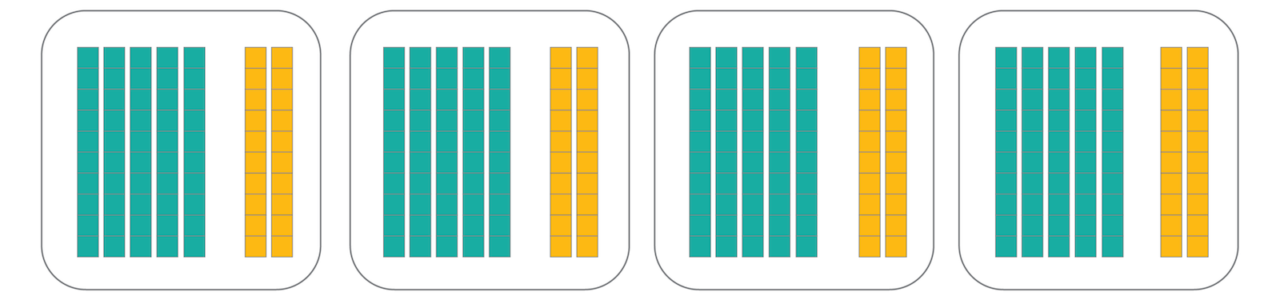
That leaves 72 units. Adding two 10s to each section is just a little bit too much because that gives a total of 280.
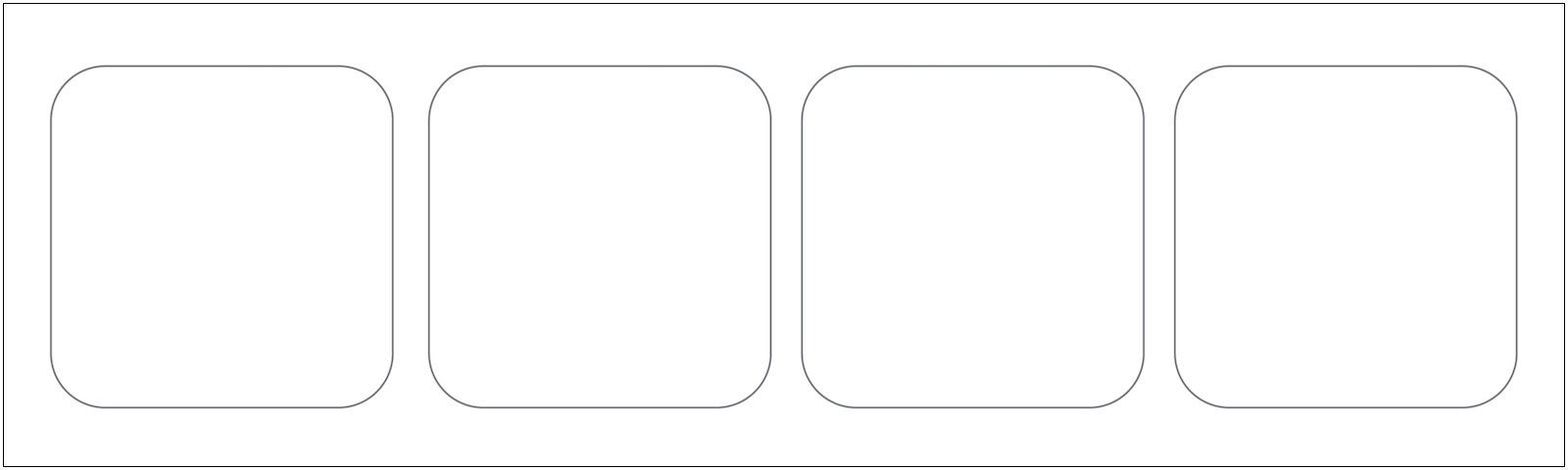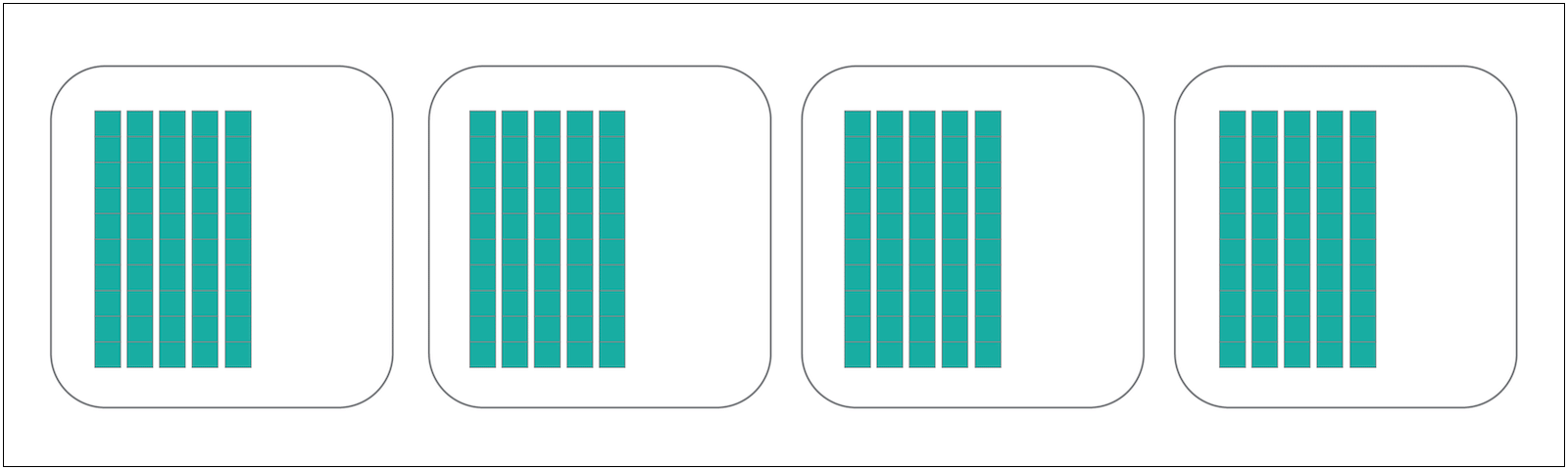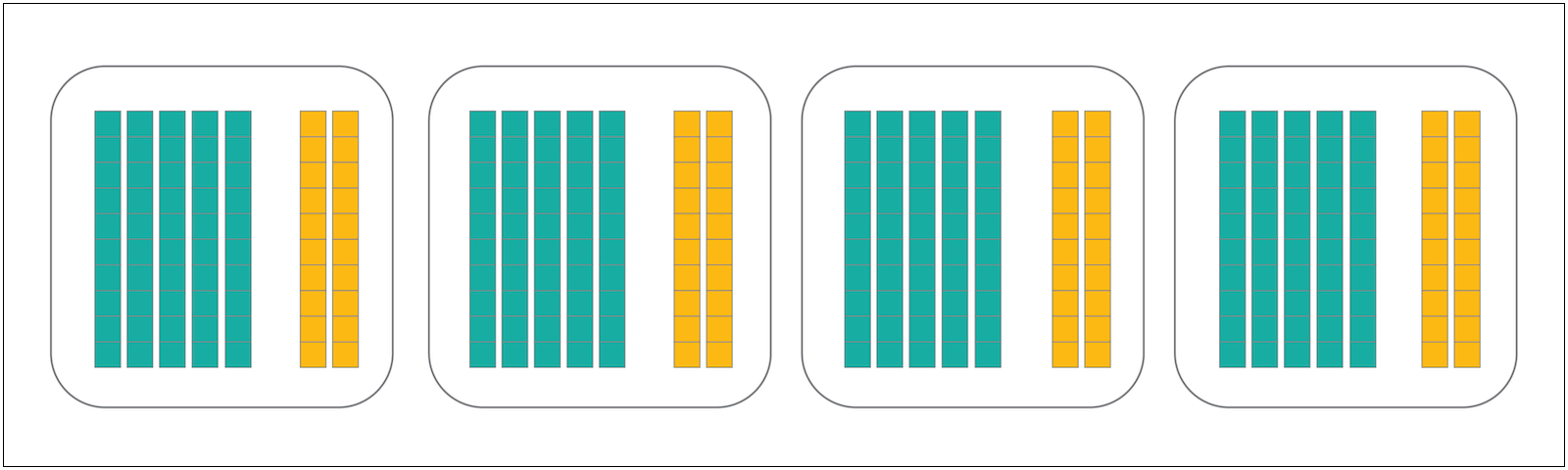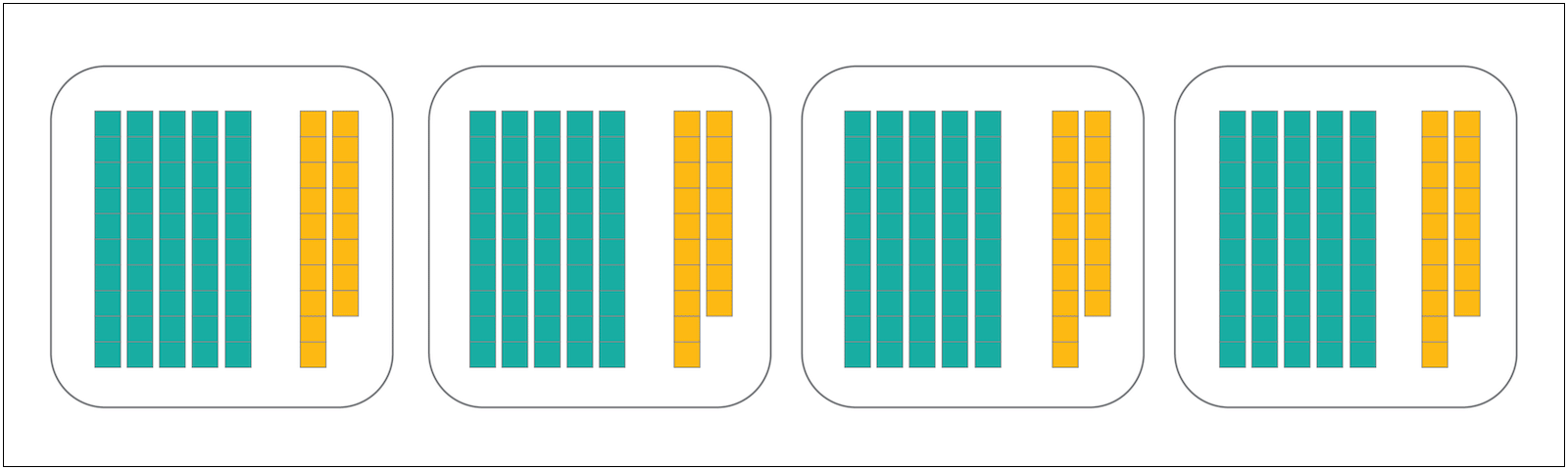
Because 280 is 8 units too much, taking away just two units from each section does the trick. So every section needs six 10s and eight 1s for a total of 272, giving us a quotient of 68.
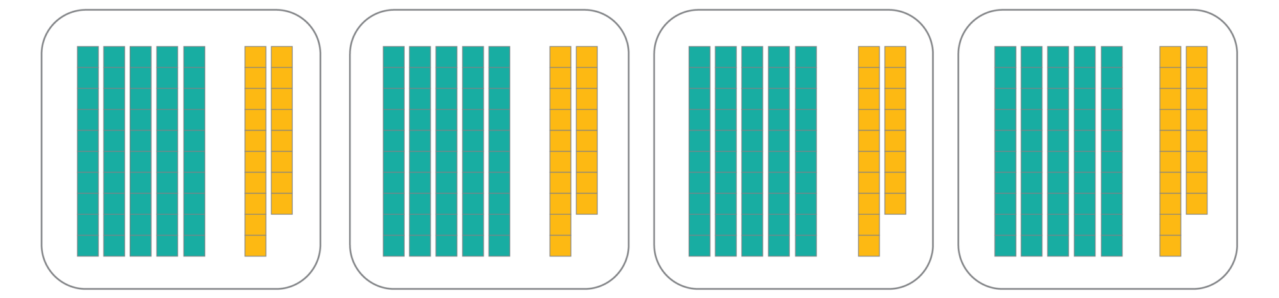
Take a look at the whole progression of discovering that 272 divided by 4 is 68!
Strategy 2: Standard Algorithm
This is the bane of students everywhere and the reason that "long division" has been maligned as silly convoluted rules that comprise math. It is also the way that many adults today (including me!) default to dividing two numbers. It's what we were taught, and it works well in most cases.
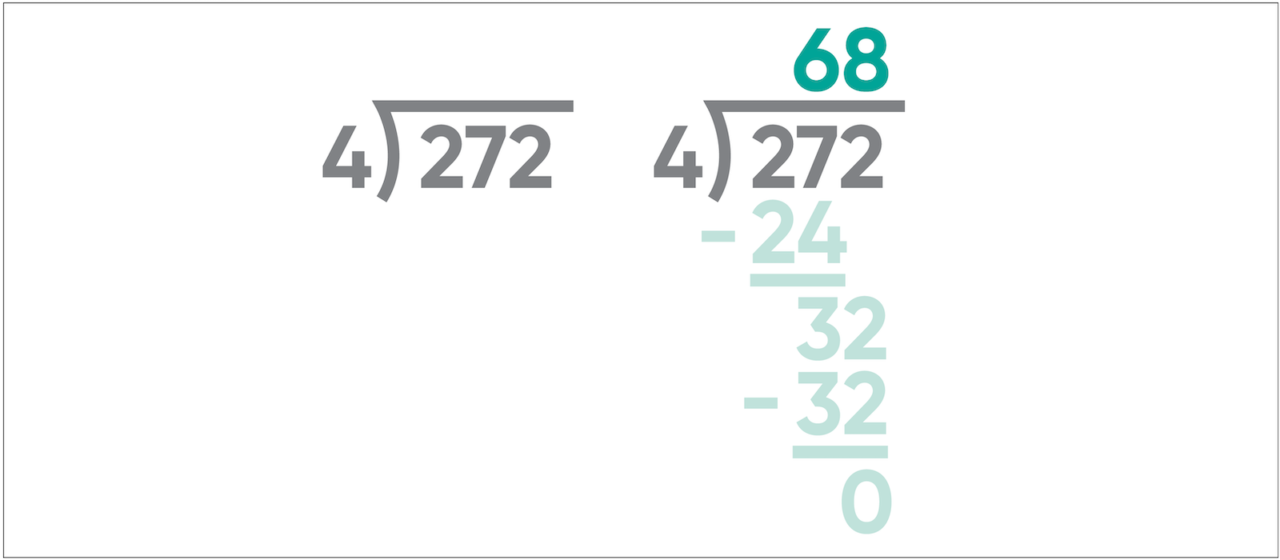
Many educators avoid teaching this algorithm altogether, and with good reason. It does not effectively illuminate the “why” behind the “what.” However, some educators also lean into the standard algorithms, recognizing them as ubiquitous tools and part of achieving math literacy. There is value in showing, for example, that the quotient begins with “6” because 6 tens are needed to divide 27 tens into 4 equal parts, with 3 tens left over.
Strategy 3: Expanded Notation Method
For many, this is the “new math.” Teachers and parents alike are sometimes turned off by this method because it looks alien compared with the standard algorithm they’re used to. However, it is simply another algorithm that will produce the desired quotient and, in particular, better reveal the mechanics behind why the algorithm works.
To divide 272 by 4, begin with the dividend inside a division box and the divisor outside it, just like the standard algorithm.
Now look for any number that you can multiply 4 by that stays under 272. For example, 4 times 50 is 200. Write the partial quotient above the division line and subtract the partial product. That leaves us with 72.
Now continue the process, looking for partial products that stay under 72. 4 times 10 is 40, which is less than 72. And finally, 4 times 8 is exactly 32. Add up the partial quotients, whatever they are, to get the final quotient. In this case, 50 + 10 + 8 = 68.
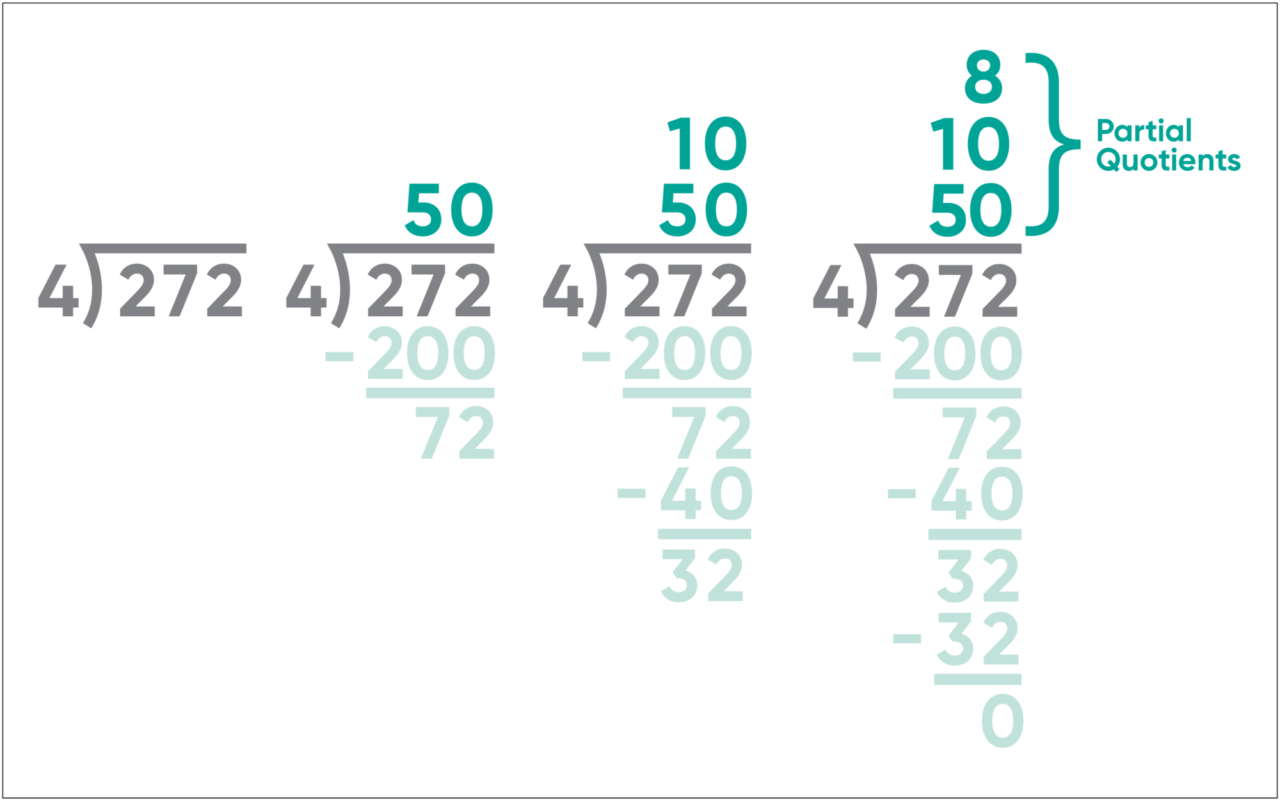
Strategy 1, which is a great tool for introducing the idea and catering to the fact that people learn best visually, is adapted from HMH Into Math (Grade 4, Lesson 7.2). Strategy 2 is a pervasive way that students will see division outside of math class and is adapted from Math in Focus (Grade 4, Lesson 3.4). Strategy 3 works even when the numbers get large or complicated and allows for more individual student approaches. This is adapted from the inquiry-based Math Expressions (Grade 4, Lesson 3.2).
No matter what program you use, the more ways that students can explore division, the deeper their understanding will be. Try this in your classroom: Tell your students to imagine that they are business owners and have $272 to give equally to their 4 employees. Ask them to draw a picture showing how they will divide the money. How many pictures do you get?
***
Learn more about how HMH not only supports different solutions to math problems but also offers comprehensive solutions across all Pre-K–12 math classrooms.

















