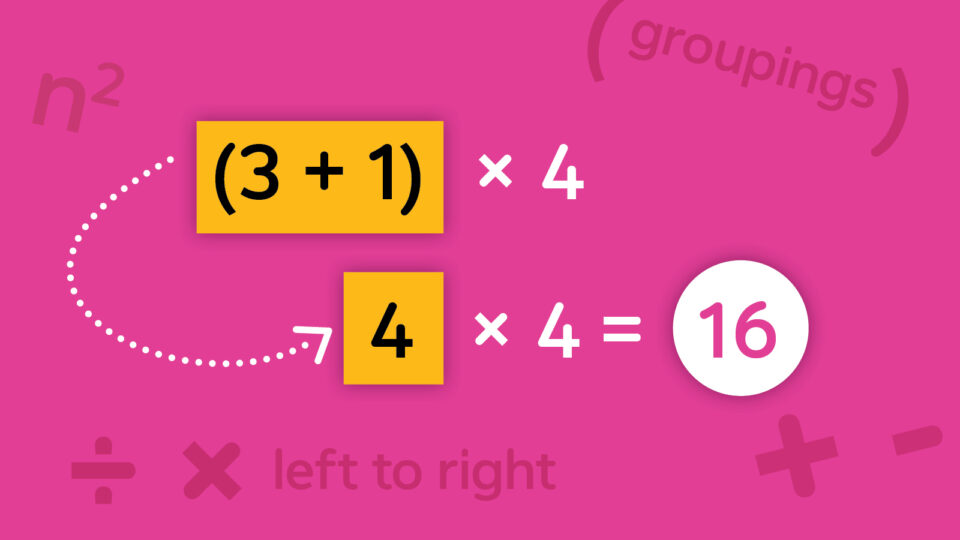
When students in Grades 3 and up initially learn to add, subtract, multiply, divide, and work with basic numerical expressions, they begin by performing operations on two numbers. But what happens when an expression requires multiple operations? Do you add or multiply first, for example? What about multiply or divide? This article explains what order of operations is and gives you examples that you can also use with students. It also provides two lessons to help you introduce and develop the concept.
Key Standard:
- Perform arithmetic operations involving addition, subtraction, multiplication, and division in the conventional order, whether there are parentheses or not. (Grade 3)
The order of operations is an example of mathematics that is very procedural. It's easy to mess up because it's less a concept you master and more a list of rules you have to memorize. But don't be fooled into thinking that procedural skills can't be deep! It can present difficult problems appropriate for older students and ripe for class discussions:
- Does the left to right rule change when the multiplication is implied rather than spelled out? (For example, \(3g\) or \(8(12)\) instead of \(3 \times g\) or \(8 \cdot 12\).)
- Where does factorial fall within the order of operations?
- What happens when you have an exponent raised to another exponent, but there are no parentheses? (Note that this lesson does not include exponents, although if students are ready, you can expand your lesson to include them.)
What Comes First in Order of Operations?
Over time, mathematicians have agreed on a set of rules called the order of operations to determine which operation to do first. When an expression only includes the four basic operations, here are the rules:
- Multiply and divide from left to right.
- Add and subtract from left to right.
When simplifying an expression such as \(12 \div 4 + 5 \times 3 - 6\), first compute \(12 \div 4\) since the order of operations requires first evaluating any multiplication and division (whichever comes first) from left to right before evaluating addition or subtraction. In this case, that means first calculating \(12 \div 4\) followed by \(5 \times 3\). Once all multiplication and division have been completed, continue by adding or subtracting (whichever comes first) from left to right. The steps are shown below.
| \(12 \div 4 + 5 \times 3 - 6\) | |
| \(3 + 5 \times 3 - 6\) | Because \(12 \div 4 = 3\) |
| \(3 + 15 - 6\) | Because \(5 \times 3 = 15\) |
| \(18 - 6\) | Because \(3 + 15 = 18\) |
| \(12\) | Because \(18 - 6 = 12\) |
Consider another expression as an example:
| \(6 + 4 \times 7 - 3\) | |
| \(6 + 28 - 3\) | Because \(4 \times 7 = 28\), which is done first because multiplication and division are evaluated first. |
| \(34 - 3\) | Because \(6 + 28 = 34\) |
| \(31\) | Because \(34 - 3 = 31\) |
Sometimes we might want to ensure addition or subtraction is performed first. Grouping symbols such as parentheses \(( )\), brackets \([ ]\), or braces \(\{ \}\), allow us to determine the order in which particular operations are performed.
The order of operations requires that operations inside grouping symbols are performed before operations outside them. For example, suppose there were parentheses around the expression 6 + 4:
| \((6 + 4) \times 7 - 3\) | |
| \(10 \times 7 - 3\) | Because \(6 + 4 = 10\), which is done first because it's inside parentheses. |
| \(70 - 3\) | Because \(10 \times 7 = 70\), and there are no more parentheses to consider. |
| \(67\) | Because \(70 - 3 = 67\) |
Notice that the expression has a totally different value! What if we put parentheses around \(7 - 3\) instead?
| \(6 + 4 \times (7 - 3)\) | |
| \(6 + 4 \times 4\) | This time, \(7 - 3\) is in parentheses, so we do that first. |
| \(6 + 16\) | Because \(4 \times 4 = 16\), and once there are no parentheses left, we proceed with multiplication before addition. |
| \(22\) | Because \(6 + 16 = 22\) |
This set of parentheses yields yet another answer. So, when parentheses are involved, the rules for order of operations are:
- Do operations in parentheses or grouping symbols.
- Multiply and divide from left to right.
- Add and subtract from left to right.
Introducing the Concept: Order of Operations
Before your students use parentheses in math, they need to be clear about the order of operations without parentheses. Start by reviewing the addition and multiplication rules for order of operations, and then show students how parentheses can affect that order.
Materials: Whiteboard or way to write for the class publicly
Prerequisite Skills and Concepts: Students should be able to evaluate and discuss addition, subtraction, multiplication, and division expressions.
- Ask: What operation do I perform first in the expression \(5 \times 7 + 3\)? Why?
Write the expression publicly. If students disagree, have them explain without telling them whether they're right or wrong. If needed, remind them that in the order of operations, multiplication and division come before addition and subtraction.
- Ask: What is the value of this expression?
Walk students through evaluating the expression. \(5 \times 7 = 35\), so the expression becomes \(35 + 3\), which equals \(38\).
- Ask: What happens if I switch the addition and multiplication symbols? What value would I get?
Rewrite the expression as \(5 + 7 \times 3\), and work through the evaluation. \(7 \times 3 = 21\), so the expression becomes \(5 + 21\), which equals \(26\).
- Ask: Did we get different values when we changed the operations?
This result will probably not surprise your students. They most likely know that performing different operations on the same numbers will give different values. If time permits and students are ready, challenge them to find an expression where switching the addition and multiplication symbols like you did results in the same value. If any students succeed, have them show how they derived the expressions. Note that it is only possible when the middle number is 1 (e.g. \(5 \times 1 + 3\) or \(5 + 1 \times 3\)) or the outside numbers are equal (e.g. \(3 \times 7 + 3\) or \(3 + 7 \times 3\)).
- Ask: What if I wanted to keep the multiplication and addition symbols in the same place (\(5 \times 7 + 3\)) but perform \(7 + 3\) first? How do you think I could do that?
Discuss the question for a short time, then write \(5 \times (7 + 3)\) on the board. Draw attention to the parentheses.
- Say: We call these symbols parentheses. If there are parentheses in an expression, do whatever is inside the parentheses first.
- Ask: What is inside the parentheses in the expression \(5 \times (7 + 3)\)?
Make sure that students can correctly identify that \(7 + 3\) is inside the parentheses and that it should be evaluated before computing with the \(5\).
- Say: Now, let's finish calculating the value. (The value is \(5 \times 10\), or \(50\).) Is that the same value we got before?
Help students notice that the value isn't the same as either the original expression or the expression with the operation symbols switched.
This would be a good moment to discuss the mathematical practice of attending to precision. In math, it is critical that we are deliberate when writing mathematical expressions and making mathematical statements. Small mixups with the math rules of operations or parentheses can cause drastic changes! Imagine incorrectly evaluating an expression when calculating a medicine dosage or a cost, for example.
Give students a few more examples, showing an expression with and without parentheses. Have student volunteers evaluate the expressions and compare their values. When students arrive at different values, avoid telling them they are right or wrong. Instead, have them find similarities and differences in their strategies, and guide the discussion so that students can see which strategy matches the rules for order of operations.
Developing the Concept: Order of Operations
Materials: Whiteboard or way to write for the class publicly
Prerequisite Skills and Concepts: Students should be familiar with order of operations and feel prepared to practice it.
As you continue teaching your students about parentheses, be sure to demonstrate that parentheses do not always change the value of an expression, though they often do.
- Ask: What operation do I perform first in the expression \(3 + 5 \times 8\) and why?
Write the expression publicly. Make sure students understand clearly that the order of operations requires them to perform multiplication before addition.
- Ask: What happens if I want to add 3 and 5 before I multiply by 8?
Allow students to discuss ideas of how to override the order of operations. Do not tell students that they are right and wrong. Instead, encourage mathematical discourse and compare differing opinions in order to correct misconceptions. Note that there are many possible answers! For example, the problem could explicitly say "add 3 and 5 first," or historically, there have been other ways of grouping, such as using horizontal bars over the expression. If they don't mention parentheses, remind them of what you did in the first lesson.
- Say: By putting parentheses around \(3 + 5\) we are saying that we must add 3 and 5 first, then multiply by 8. Today we're going to practice finding the value of expressions with and without parentheses and see what difference the parentheses make.
- Write the following three expressions publicly for all students to see.
- \(3 + 6 \times 2\)
- \((3 + 6) \times 2\)
- \(3 + (6 \times 2)\)
- Say: Calculate all three expressions.
Allow time for students to finish calculating. Then have student volunteers report what they found.
- Ask: Did you get the same value for all three expressions? Why or why not?
Students should notice that expressions 1 and 3 yield the same value while expression 2 is different. Discuss that expression 2 requires that we add before multiplying while expressions 1 and 3 have us multiply before adding. The goal is for students to see that the use of parentheses sometimes changes the value of an expression and sometimes doesn't.
- Write the following two expressions publicly for all students to see.
- \((8 \div 4) - 2\)
- \(8 \div (4 - 2)\)
- Say: Calculate both expressions.
Allow time for students to finish calculating. Then have student volunteers report what they found.
- Ask: Are the values of these expressions the same? Why or why not?
Once again, students should see the significance of the use of parentheses.
- Say: Now we are going to try an activity with many possible solutions. Your goal is to find an expression where you can move the parentheses without changing the value. The challenge is the parentheses must be around addition or subtraction.
Walk through an example. Show how in the two expressions below, the parentheses are around an addition expression, and when they're moved, the expression's value stays the same: 7.
- \((3 + 4) \times 1\)
- \(3 + (4 \times 1)\)
- If feasible, have students work in pairs to create additional examples. For students who are stuck, have them try replacing the 3 and/or the 4 in the expressions above.
- Ask: How did you create expressions that allowed you to "move" the parentheses? What problems did you run into?
Facilitate a discussion around the different expressions students made. Have students compare similarities and differences both in the expressions they made and the strategies they used to make them.
Wrap-Up and Assessment Hints
It is important that students can remember the rules for order of operations both with and without parentheses. Avoid giving worksheets of rote practice. Instead, look for math problems that naturally result in expressions that need to be evaluated, for example substituting values into a formula, and have students practice order of operations in the context of other problems.
***
Looking to grow student confidence in mathematics, beyond practicing the math rules of order of operations? Explore HMH Into Math, our K–8 core mathematics solution.
