One persistent challenge of math teachers everywhere is showing that math is relevant and important. It is all around us, even when we don’t notice it, and it is important in science, social studies, and even art! Back in January, we posted three activities that K–12 math teachers can use to teach math using art from the Metropolitan Museum of Art.
Math at The Met: A New Video
We’re back, and this time with a video! In our first episode, discover how different numbers look around the world and throughout history. In the video, we explore art from Ancient Egypt and India, along with 17th-century England, especially the different ways that numbers were represented.
Click the image below to play the full video.
Below are five ways to organize activities and facilitate mathematical discourse using ideas discussed in the video. These range from 5-minute warm-up discussions to full-class activities. We recommend reviewing the ideas in advance and choosing the ones that are right for you and your students.
In this part of the video, we see a number written into an ancient Indian tile. Going from bottom to top are the symbols for 5, 4, and 10. Combined, this is the number 19.
Activity: Decorate a Building (Grades 3–5)
Have students decorate their own building! Or at least a wall or section. Begin by having them draw the design on their own paper. Then, have them cut the design into evenly-shaped pieces. Finally, have them number the pieces. For students who are ready, instead of labeling the pieces “1,” “2,” “3,” and so on, have them use Roman or Kharosthi numerals or invent their own numbering system. Now, can a classmate recreate the design? One way to do this activity digitally is to take a picture of the pieces, send the photo(s) to a classmate, then have them draw the completed design.
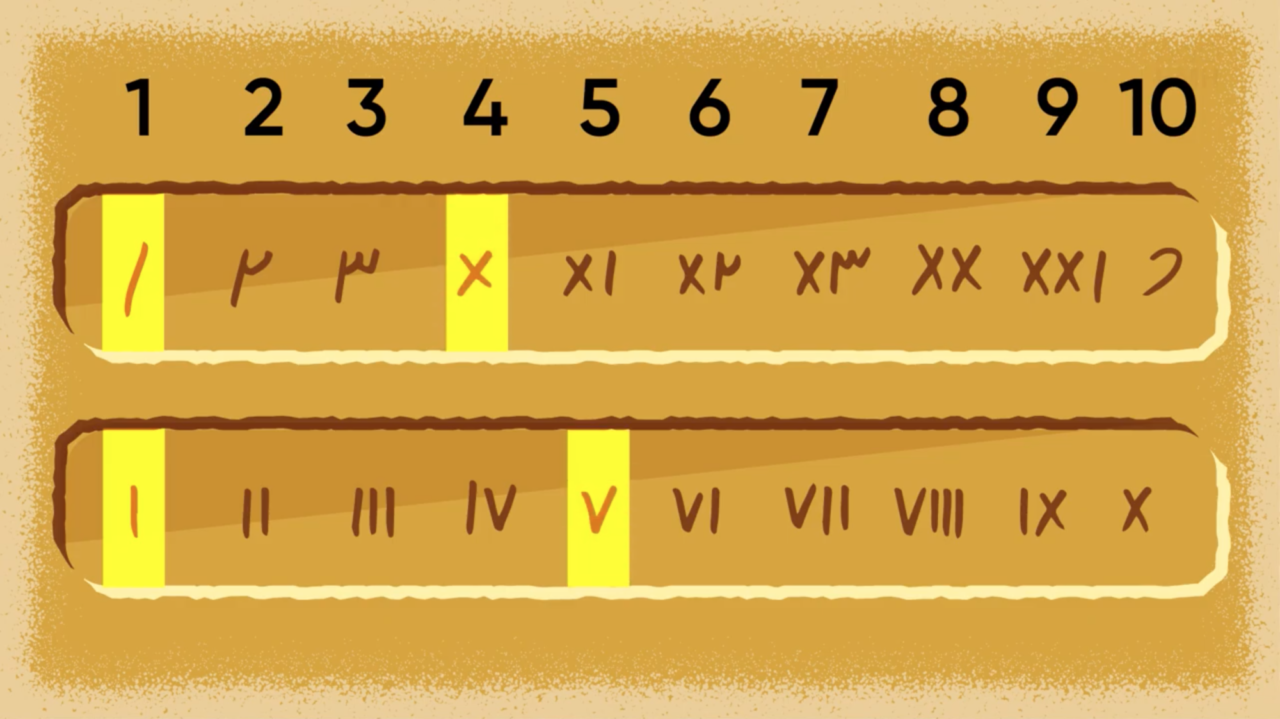
Here we see the Kharosthi numerals for 1–10 (top row) along with the Roman numerals (bottom row). Notice that 1 and 4 (top) and 1 and 5 (bottom) are highlighted. That's to draw attention to the distinct symbols being used.
Discussion: Symbols (Grades 3–6)
This is an opportunity to facilitate discourse around math in the classroom, especially if students have been previously introduced to Roman numerals. Call specific attention to which numbers get their own unique symbol (like "V") as opposed to being made from different symbols (like "IV"). Ask the following questions, and avoid calling anything right or wrong. Instead, call attention to similarities and differences among different student answers.
- What are advantages to having a unique symbol for 4 (as in Kharosthi script), as opposed to having a unique symbol for 5 (as in Roman numerals)?
- What other options are there for choosing the unique symbols?
- How would those other options change what the number 5 looks like? 10? 50? How would it change how numbers look in general?
Here we see how to represent the numbers 1–10, along with 100; 1,000; 10,000; 100,000; and 1 million, in hieroglyphics.
Discussion: Roman Numerals (Grades 3–6)
This is another opportunity to facilitate discourse around math in the classroom. Ask the following questions, and avoid calling anything right or wrong. Instead, call attention to similarities and differences among different student answers.
- In the video, why does the host say that Roman numerals “really only have three symbols between 1 and 10,” referring to I, V, and X?
- What are some different ways for writing the same number? (For example, “IIII” and “IV” or “VIIII” and “IX”)
- What are new rules you can invent for writing numbers? (For example, putting a circle over a symbol means to double it)
Extend this discussion into a complete lesson by having students invent their own writing system! We describe this lesson in our previous blog post.
Here we see how to write “eternity” using Egyptian hieroglyphics: as “1,100,000 years.” This is an example of taking an exact number (1,100,000) and giving it an inexact meaning ("eternity").
Discussion: Language and Math (Grades 3–12)
For these discussion questions, students will explore how language is used to describe numbers. Prepare a list in advance of ways that we use different words and phrases to represent quantities. Depending on the students, consider words for fractional quantities, decimal numbers, variables, or operations. Avoid calling anything right or wrong. Instead, call attention to similarities and differences among different student answers.
- Can you think of examples of English words with specific mathematical meaning? (Examples: pair, duo, quartet, dozen)
- Can you think of examples of specific numbers with a looser English meaning? (Examples: “I’ll be done in a second.” “Talk to you in a minute.” “That’ll take me a million years!”)
- Do any of your students speak languages other than English? Can they think of any examples in those languages?
Here we see all of the different numbers discussed in the video: Western Arabic (what we use in the U.S.), Eastern Arabic, Kharosthi, and Roman. This lets you compare many numeral systems at once.
Discussion: Zero (Grades 3–6)
In both Roman numerals and Kharosthi script, the number “100” is represented with just one symbol; whereas, we use three (“1,” “0,” and “0”). However, the number "89" requires nine symbols in Roman numerals (“LXXXVIIII”), but just two for us (“8” and “9”). Show these examples to students and ask the following questions. Avoid calling anything right or wrong. Instead, call attention to similarities and differences among different student answers.
- Why does having a zero make the number for 89 shorter to write with modern numbers and 100 longer?
- Why does having a zero make writing numbers easier overall? (Hint: Think about very, very large numbers.)
***
Itching for similarly engaging math activities? How about math on a fashion runway or at the Olympic Games? Explore math throughout high-interest careers in our Math at Work web series.
