
If there’s one question that every math teacher has gotten in their lives, it’s “Why does math matter?”
We learn to read and see words everywhere. We learn a language and can then talk to new people. We see and experience science, music, art, and history. But what about math? Where does math show up in the real world?
Often, the problem is that students see math as rules to follow and equations to solve. But math is a language, a way of thinking, and an expression of our humanity.
And where better to see humanity on full display than at the Metropolitan Museum of Art (or The Met), the fourth largest museum in the world with objects dating from the 8th millennium BC to today? Here are three ways that teaching math through art from The Met can enhance your students’ learning experience.
Math at The Met video
In this video, discover how different numbers look around the world and throughout history. We'll explore art from Ancient Egypt and India, along with 17th-century England, especially the different ways that numbers were represented.
Click the image below to play the full video.
Below are some activities, pulled from our blog dedicated to the Math at The Met video, that facilitate mathematical discourse. These range from 5-minute warm-up discussions to full-class activities. We recommend reviewing the ideas in advance and choosing the ones that are right for you and your students.

In this part of the video, we see a number written into an ancient Indian tile. Going from bottom to top are the symbols for 5, 4, and 10. Combined, this is the number 19.
Activity 1: Decorate a building (Grades 3–5)
Have students decorate their own building! Or at least a wall or section. Begin by having them draw the design on their own paper. Then, have them cut the design into evenly-shaped pieces. Finally, have them number the pieces. For students who are ready, instead of labeling the pieces “1,” “2,” “3,” and so on, have them use Roman or Kharosthi numerals or invent their own numbering system. Now, can a classmate recreate the design? One way to do this activity digitally is to take a picture of the pieces, send the photo(s) to a classmate, then have them draw the completed design.
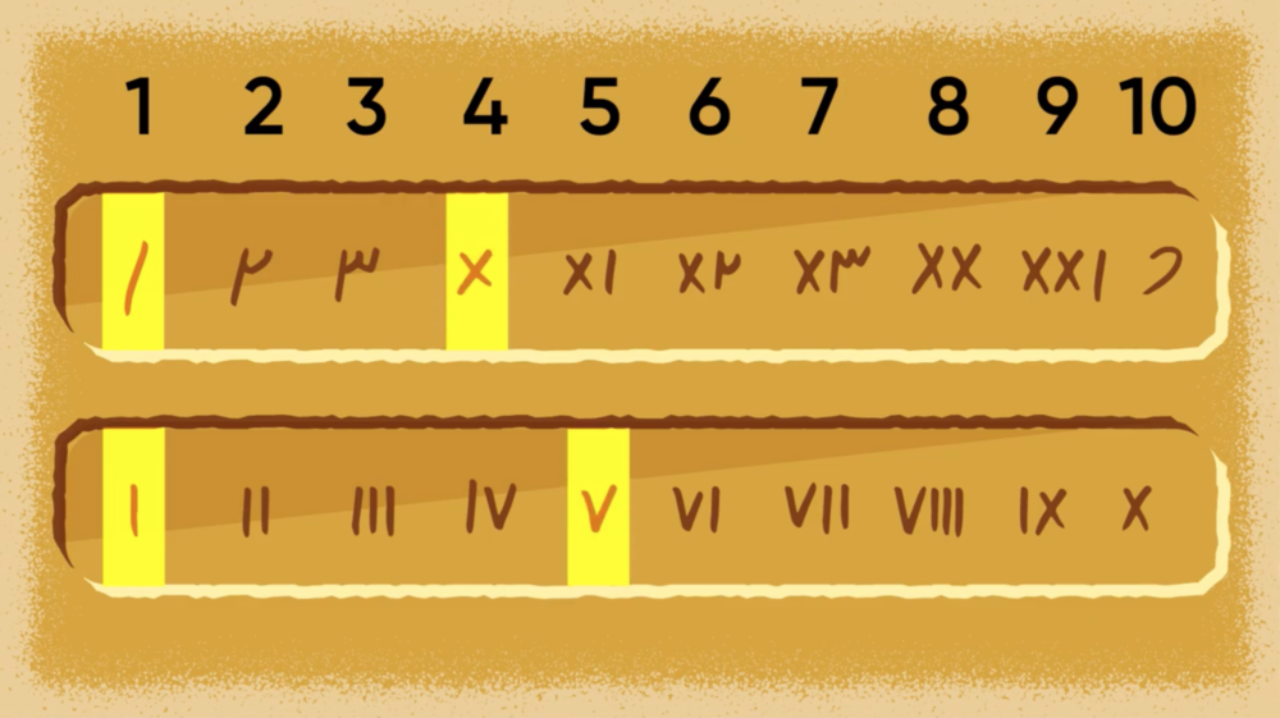
Here we see the Kharosthi numerals for 1–10 (top row) along with the Roman numerals (bottom row). Notice that 1 and 4 (top) and 1 and 5 (bottom) are highlighted. That's to draw attention to the distinct symbols being used.
Activity 2: Language and math discussion (Grades 3–12)
Below we see how to write “eternity” using Egyptian hieroglyphics: as “1,100,000 years.” This is an example of taking an exact number (1,100,000) and giving it an inexact meaning ("eternity").

For these discussion questions, students will explore how language is used to describe numbers. Prepare a list in advance of ways that we use different words and phrases to represent quantities. Depending on the students, consider words for fractional quantities, decimal numbers, variables, or operations. Avoid calling anything right or wrong. Instead, call attention to similarities and differences among different student answers.
- Can you think of examples of English words with specific mathematical meaning? (Examples: pair, duo, quartet, dozen)
- Can you think of examples of specific numbers with a looser English meaning? (Examples: “I’ll be done in a second.” “Talk to you in a minute.” “That’ll take me a million years!”)
- Do any of your students speak languages other than English? Can they think of any examples in those languages?
Activity 3: Create your own writing system (Grades 3–5)
The Met’s collection goes back in history. Way back. This necklace, for example, is more than 4,000 years old!

The pectoral (central pendant hanging from the necklace) has very stylized hieroglyphics that read, “The god of the rising sun grants life and dominion over all that the sun encircles for eternity to King Senusret II.” However, the way the ancient Egyptians write eternity is “one million, one hundred thousand years.” Similar to how we may use the phrase “a million years” in English to mean a few hours or days, the ancient Egyptian language uses a specific number to have a non-specific meaning.
Ancient hieroglyphics represented base 10 without the digit zero. Instead, they had unique symbols for every power of 10 (1; 10; 100; 1,000; and so on) and repeated them to show multiples. For example, the number 327 would have the “100” symbol written three times, the “10” symbol two times, and the “1” symbol seven times.

Here’s another number in ancient hieroglyphics: The number 1,100,000 is a combination of a man raising his arms and a tadpole dangling from his right arm.

Create your own writing system
- Materials: Pencil and paper
- Key standard: Recognize that in a multi-digit whole number, a digit in one place represents ten times what it represents in the place to its right. (4.NBT.A.1)
- Have all students make their own symbols for 1, 10, 100, and 1,000 (or as high as you would like). Depending on the students’ ages, consider letting them invent entire rules for creating numbers as well, like how Roman Numerals use III for 3 but IV for 4.
- Have each student write the following numbers in their new writing system. Substitute with different numbers if you would like:
- 327
- 307
- 1,483
- 1,080
- 7,989
- Show the numbers one at a time, then have every student hold up what they drew. Does everyone have the same number of symbols? If not, whose is the shortest? The longest? Have students look for similarities and differences.
Activity 4: Draw a hypercube (Grades 5–8)
Are you teaching two- and three-dimensional shapes? Why not teach four? Using art in math lesson plans helps students visualize complex concepts, like four-dimensional space, and answer questions such as, “What exactly is a dimension? How do we abstract it?” The Met includes one of Salvador Dalí’s best-known paintings: Crucifixion, featuring a hypercube similar to the image below.

Draw a hypercube
- Materials: Pencil and paper
- Key standard: Represent three-dimensional figures using nets made up of rectangles. (6.G.A.4)
- Show students how a point is zero-dimensional, a line segment is one-dimensional, a square is two-dimensional, and a cube is three-dimensional. Ask them: How would you draw the “next” picture?

- Show students one way to do it: Draw a cube as a two-dimensional net. In the Dalí painting, we see a three-dimensional net of a four-dimensional hypercube.
- Can students find another way to do it? Urge them to try on their own and promise not to look up anything online unless they’re stuck for at least 15 minutes.
- Have students share what they drew. What similarities do other students notice? What do these drawings make them wonder?
Activity 5: Create a wall drawing (Grades K–12)
Artists must attend to great precision, which is another way that math manifests itself in art. This is, in some ways, more significant than a math standard; it’s a math practice. If you’re looking for art that can help display how to use a ruler and divide fractions, check out Sol LeWitt’s Wall Drawing #370, where the artwork is, in fact, a set of strict rules that someone must follow when painting a wall. You can find the artwork, similar to the recreation below, on one of The Met’s walls.

Create a wall drawing
- Materials: Blank sheet of paper, a variety of tools for writing and drawing such as pencils and markers, ruler, and calculator or computer
- Key standard: Attend to precision. (Math Practice 6)
- One student creates a set of rules for another student to follow. Here are some examples to consider (for varying grades):
- Divide the page into an array of three rows and two columns.
- Draw a vertical line every 1 2/3 inches.
- Draw a heptagon inside every rectangle.
- Interpret the rectangles as the first quadrant of a coordinate grid, where the tick marks represent distance in millimeters. Graph f(x) = arctan(x).
- Use a green pen.
- Every student then creates two artworks on their own using two other students’ rules.
- Go around the class, having each student share how their art got made.
- Whose pair of artworks looked the most similar? Whose pair looked the most different? Why?
***
Using art to teach math shows students how math can be just as exciting and creative as art. Itching for more engaging math activities like “Math at The Met?” How about math on a fashion runway or at the Olympic Games? Explore math throughout high-interest careers and endeavors in our Math at Work web series.
This blog, originally published in 2021, has been updated for 2025.
Get our FREE guide “Optimizing the Math Classroom: 6 Best Practices.”












