7 Strategies for Math Language Routines

Math and language

In 1623, Italian scientist Galileo Galilei published The Assayer, in which he famously wrote that the universe is “written in the language of mathematics.” (Or rather, he wrote that it’s scritto in lingua matematica.) What he meant was that the laws of nature found in sciences like physics and chemistry are often expressed using the “language” of math, making math a language in its own right.

While this may be true for many scientists, the math that schoolchildren learn is more than just numbers and formulas and requires a lot of language in the traditional sense. Consider the ubiquitous word problem or all of the linguistic background needed to understand why “twelve times eighteen“ is logically equivalent to the very different-looking phrase “the product of a dozen and six tripled.” Students need language to ask questions, and teachers need language to explain ideas.

This connection between language and math has long attracted teachers and education researchers, with clear evidence that students’ development of one predicts development of the other. “Language has long been hypothesized to play a pivotal role in mathematical development,” write Daniel Espinas and Lynn Fuchs in a research study on the effects of language instruction on math development. They walk through a variety of “both obvious and unexpected ways” that the two domains are connected:

• Word problems: One of the most direct examples of written language showing up in math class is the word problem, where students convert written language to mathematical representations and use those representations to solve the problem.
• Vocabulary knowledge: Success in mathematics requires learning a variety of vocabulary terms. Think words like “sum,” “more,” or “hypotenuse.”
• Syntactic knowledge: The language spoken and written in math class involves many examples of understanding the language’s syntax, or how individual language components combine to form meaning. Think of how the adjective “one” vs. “two” changes the noun that follows, or the difficulties in explaining how “eighteen” means 8 + 10 and “nineteen” means 9 + 10, whereas “eleven” and “twelve” don’t follow this linguistic pattern. (At least not in English!)
• Phonological processing: This refers to hearing, remembering, and repeating how language sounds. Consider how teaching the meaning of an equation like 3 + x = 11 requires being able to understand and interpret the spoken sequence “three plus x equals eleven.”
• Number knowledge: Over the course of math instruction, students must be familiar with not only precise uses of numbers like “six meters” or “one thousand people” but also imprecise uses, such as “few,” “about,” or “less.”

Routines for the classroom

Math teachers likely already have many rituals and routines that they use. This includes general routines to manage orderliness and behavior, such as getting out computers or switching materials between classes. This also includes routines that happen during instruction, such as think-pair-share, a versatile strategy that can be called upon to provoke thoughtful discussion.

“Establishing routines and procedures is a crucial, effective strategy for better classroom management,” writes Katie Risolo Radovich, a first-grade teacher in New York. They can help a classroom feel like a positive, familiar environment and help to ensure that students focus on the problem at hand rather than logistical details around whom to partner with or what materials to use.

What are math language routines?

Language-focused routines can be an important tool in a math teacher’s toolkit. Learning to communicate mathematical ideas effectively is a critical part of learning math that helps clear up misconceptions along the way. Routines can focus on discourse, vocabulary, writing, and the different ways that math and language interact. In this sense, math language routines fit into a larger body of routines aimed at helping students stay engaged and experience academic growth.

Math language routines can take a lot of forms, with several possible strategies listed below. In general, the routine will involve steps that are repeated every time, making it easier for teachers to plan and students to stay focused. They generally involve some sort of set-up, such as showing a diagram or asking a question, along with repeatable tasks to complete, such as silently writing for a specified amount of time.

The importance of math language routines

Learning the “language” of math isn’t possible without using a more traditional language (like English). Students and teachers both need a language to communicate in so they can read, write, speak, and listen about math. Ideally, students practice the language of mathematics year-round by engaging in mathematical discourse, writing about math, and solving complex word problems.

The routines themselves can have a variety of different purposes, for example they could be about fostering meta-awareness or taking a starting piece of mathematical writing and optimizing it. Into Math and Into AGA, HMH’s math solutions for kindergarten through Algebra 2, include a variety of language routines aimed at helping students stay engaged and experience academic growth. These routines, which are described below, are grounded in research and provide opportunities for students at all proficiency levels.

7 strategies for math language routines

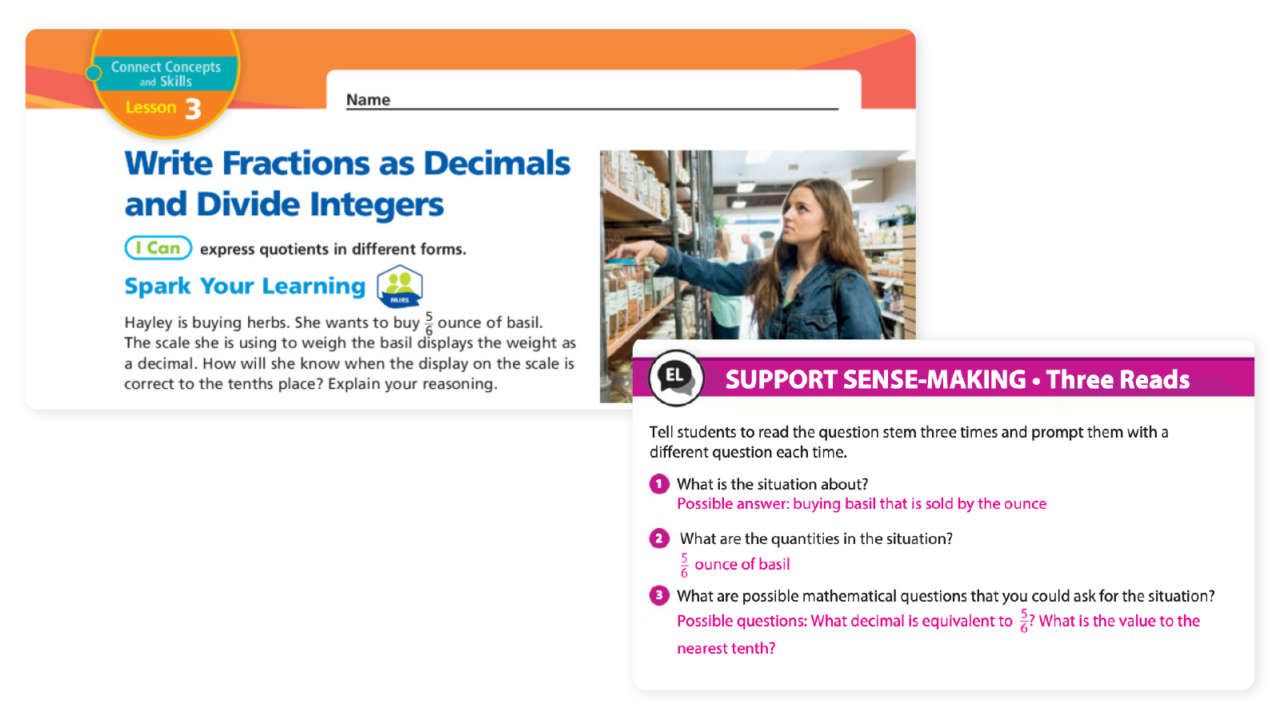
1. Three Reads

For word problems, Three Reads helps to break down the context of a problem and guide students in focusing on one aspect of the language at a time. To use this routine, read the problem three times, but with a different focus on each read:

• First read: Focus only on understanding what the problem is asking.
• Second read: Focus on specifically understanding the mathematics of the problem.
• Third read: On the final read, focus on the specific question being asked and brainstorm possible mathematical questions that pertain to the problem.

This routine supports students in comprehending word problems, as it scaffolds making sense of all of the information that needs to be gleaned from the problem. Students consider the mathematical language of a problem critically and take the time to ensure it makes sense to them.

2. Stronger and Clearer Each Time

This routine is designed to help students discuss mathematical ideas with one another. The goal is for students to strengthen and clarify their academic thoughts as students discuss them with each other. For this routine, students do not begin with a well-formed, complete solution to a problem. Real-time problem solving is often messy and incomplete. Students begin solving a problem using what they think and what they know. After sharing their ideas with different partners, they build on them and develop the language to solve the problem “stronger and clearer.”

Like Three Reads, Stronger & Clearer Each Time is especially well-suited to word problems. Students can begin the routine by writing down ideas to solve the problem before discussing it with others. Then, students are given a partner tasked with asking clarifying questions, requiring students to think carefully and deeply about their explanations. Students are then placed in successive pairings, building continually on the idea they started with. The routine can conclude with students writing down final explanations, comparing it with what they wrote at the start.

3. Compare and Connect

Compare and Connect is another routine that has students interacting with one another to gain a meta-awareness of the strategies they’re using. The routine is grounded in solving a single problem, but the discussion has students identifying, comparing, and contrasting a range of mathematical ideas and strategies for solving the problem.

To set up the routine, students are assigned partners with one partner solving a problem or representing a task in one way. The other partner then tries to work through the idea in a different way. Then, the students reflect on the two approaches, comparing and contrasting them. The goal is for students to strengthen their self-reflection skills and connect one problem or task to other concepts.

Teachers can use Talk Moves like the following to help students in making mathematical comparisons and connections:

• Did anyone solve the problem in a different way?
• Who can restate [student]’s reasoning in a different way?
• Do you agree or disagree? Why?

4. Information Gap

This routine requires two students each using premade cards. One card has a problem on it but is missing information. The other card has a data card containing the missing information. The students must work together to determine what’s needed to solve the problem and then solve it.

In gathering the information, both students are provided with prompts to help them communicate the information with one another. The student with the problem sees the sentence frames “Please tell me _____” and “I need this information because _____.” The student with the data card sees the questions “What do you need to know?” and “Why do you need this information?”

5. Collect and Display

As the name implies, this routine involves the teacher collecting then displaying student language. As students complete a task or discuss a problem, the teacher listens and creates an anchor chart by writing down what students say. This can include words, phrases, concepts, equations, and images. The students’ own words then become ways to showcase mathematical thinking and be used as references for the entire class.

This is an especially useful routine to ensure students are attending to precision. What goes on the anchor chart are the teacher’s cherry-picked highlights of what students discuss. That is, the chart features the best examples of students using precise language and carefully applying math ideas to the appropriate context.

6. Critique, Correct, and Clarify

In this routine, the teacher presents a partial explanation or solution, and then students must identify the error or ambiguity. The goal of this routine is for students to advance their own mathematical thinking and communication by analyzing a piece of mathematical writing that is not their own.

This is a common tactic for prompting mathematical discourse, as it scaffolds making sense of math content in a way that keeps a discussion focused and students engaged.

7. Co-Craft Questions

In this routine, a pair of students work together to create a problem. They first get information that should be used with the problem. The information shouldn’t be a problem in and of itself, but rather some kind of model, description, or setup that lends itself to many different problems. Imagine, for example, a picture of a spinner divided into three unequal portions and an unfilled table next to it. Students work together to create a problem that matches what they were given, with one student recording the problem and the other recording the solution.

Students then exchange problems with another pair and solve the new problems together, recording both the solution and an explanation. Once students have completed both problems, teachers can facilitate a discussion that has students comparing strategies with one another. This routine is especially valuable in helping students make sense of problems and persevere in solving them (the first Standard for Mathematical Practice), as not just the solutions but also the problems themselves come from students.

Using language routines

HMH’s core curricular programs Into Math and Into AGA embed these research-based mathematical language routines, along with plenty of other strategies and routines, into the instruction to support high-quality math discourse and writing in the classroom. And no matter what program you use, language routines are a way to ensure students are regularly and critically engaging with the math they’re learning about. The routines provided here give opportunities for students to listen, speak, read, and write about mathematics at all proficiency levels. After all, language practice is for more than ELA class!

***

HMH’s core math solution Into Math for Grades K–Algebra 1 includes language routines, real-world connections, and more that deepen students’ mathematical understanding.