At a glance
- Subject: Math
- Report Type: Research Evidence Base
- Grade Level: Elementary, Middle
Houghton Mifflin Harcourt’s Math Expressions © 2018 is a research-based, NSF-funded, comprehensive, coherent, cumulative, rigorous, balanced, and research-based mathematics program for Grades K–6. At the heart of Math Expressions is the building of a Math-Talk community. Through their experiences in this rich Math-Talk community, students reach their learning destination—the ability to use formal math methods with understanding and fluency. Built upon a foundation of mathematics education research and NSF-funded studies1 and authored by a leader in the field of mathematics education, the program is proven to be effective in raising students’ achievement.
The purpose of this document is to demonstrate clearly and explicitly the research upon which Math Expressions © 2018 is based. This research report is organized by the major strands that guided development of the program:
- Focus and coherence, with meaningful progressions of learning across grade levels
- Rigor, with high expectations for conceptual understanding and procedural fluency
- Habits of mind, with a focus on mathematical practices and problem solving
- Effective instruction through manipulatives, visual representations, and communication
- Assessment, with a focus on data-driven instruction and ongoing assessment
- Equity and access, to meet all students’ needs through differentiation and intervention
- Technology, or the purposeful use of high-quality tools and technology to support mathematics teaching and learning
Each strand is supported by research. The content, activities, and strategies presented in Math Expressions reflect what we know about teaching for mathematical understanding and align with rigorous standards.
To help readers make the connections between the research strands and the Math Expressions program, the following sections are used within each strand:
- Defining the Strand. This section summarizes the terminology and provides an overview of the research related to the strand.
- Research That Guided the Development of the Math Expressions Program. This section identifies subtopics within each strand and provides excerpts from and summaries of relevant research on each subtopic.
- From Research to Practice. This section explains how the research data are exemplified in Math Expressions.
A list of sources is provided at the end of this document.
1.Math Expressions Common Core is based upon work supported by the National Science Foundation under grant numbers ESI- 9816320, REC-9806020, and RED-935373.
Math Expressions was developed using the methods of learning science design research focused on building students’ conceptual understanding of math, interwoven with the other components of math proficiency.
The program was part of a large-scale study sponsored by the U.S. Department of Education to determine the effectiveness of four elementary math curricula on student academic achievement.
The results of the study showed that students using Math Expressions were performing at higher levels of math achievement when compared with students using similar programs. Math Expressions yielded substantial increases in test scores as well as on broader measures of understanding.
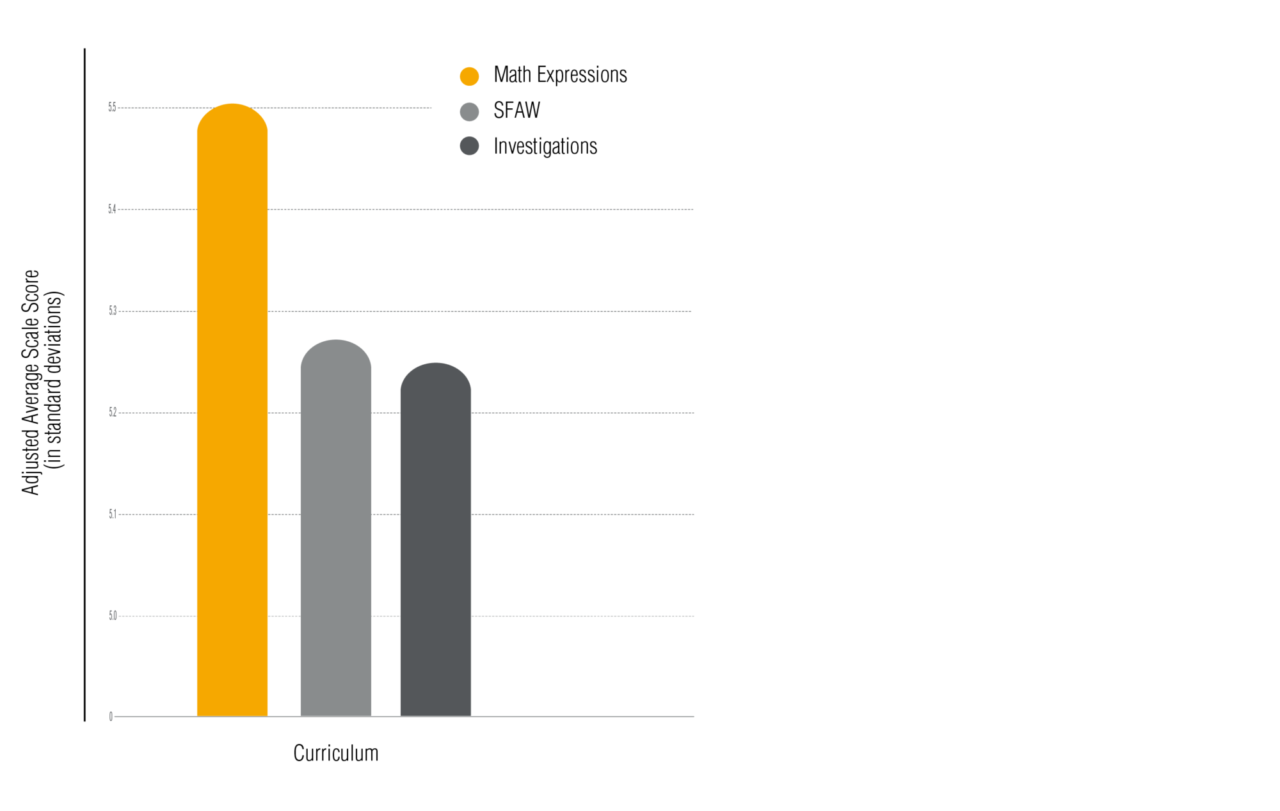
Source: Agodini, R., Harris, B., Atkins-Burnett, S., Heaviside, S., Novak, T., & Murphy, R. (2009). Achievement Effects of Four Early Elementary School Math Curricula: Findings from First Graders in 39 Schools (NCEE 2009-4052). Washington, DC: National Center for Education Evaluation and Regional Assistance, Institute of Education Sciences, U.S. Department of Education.
The Author—Dr. Karen Fuson, Professor Emerita of Education and Psychology at Northwestern University and author of Math Expressions, is a mathematics educator and developmental and cognitive scientist with decades of experience studying, researching, and writing about mathematics education.
Dr. Fuson’s research focuses on how children learn math and the classroom conditions that support the development of students’ understanding. Dr.Fuson’s research for her Children’s Math Worlds (CMW) NSF-funded project was instrumental in identifying key components for successful mathematics learning— Building Concepts, Math Talk, Student Leaders, Quick Practice, and Helping Community. The body of research that forms the basis of Math Expressions focused on the following research tasks:
- Analyzing real-world mathematical situations to help curriculum developers and teachers select problems and examples that ensure both the understanding of the general math principles at work and of the real-world situation itself
- Analyzing formal mathematical language and notation to identify difficulties that need to be addressed with pedagogical supports and classroom discussion
- Developing meaningful real-world situations and visual supports that can facilitate interest and accessibility
- Identifying meaningful language that can connect to the formal mathematical language (e.g., “break-apart partners” for addends, “unmultiplying” for dividing)
- Identifying typical student solution methods and learning paths through a domain to more-advanced solution methods
- Developing accessible, mathematically desirable algorithms that relate to common algorithms but that all students can understand and explain
- Identifying typical student errors and how to overcome them
- Choosing drawn quantity representations that can facilitate understanding of the domain situations or quantities
- Monitoring grade-level placement of, and approaches to, important topics around the world
- Writing teaching materials in a “learn while teaching” style that enables teachers to learn new ways of teaching and new solution methods
- Developing classroom activity structures that can be used repeatedly with different math topics to cut down on classroom management issues
From her research results, and collaborations with and knowledge of the research of others in the field, Dr. Fuson has designed effective teaching approaches and identified progressions of Pre-K to Grade 6 students’ development/experiential understanding across different mathematical domains. (See a list of relevant research, organized by focus, at the end of this report, in the section titled “Project References and Additional Research Support for Math Expressions.”)
In addition to the research projects described above, Dr. Fuson served on the National Research Council committees (below) that summarized research and made recommendations.
The Houghton Mifflin Harcourt® Math Expressions program is the result of this extensive research into how students learn math.
Key Research—As evidenced by the numerous studies and program references presented throughout this report, Math Expressions reflects what research shows about effective mathematics teaching and learning. The following publications present key findings foundational to the development of Math Expressions.
Adding It Up: Helping Children Learn Mathematics (National Research Council, 2001). Adding It Up presents a picture of mathematics learning from Pre-K to Grade 8.The Mathematics Learning Study Committee identifies five components of mathematical proficiency (conceptual understanding, procedural fluency, strategic competence, adaptive reasoning, and productive disposition) and presents research findings for how students develop this proficiency. The book provides key recommendations for specific changes and approaches in teaching, curricula, and teacher education that can improve students’ mathematics learning.
How Students Learn: Mathematics in the Classroom (National Research Council, 2005). This publication was written to build upon the earlier How People Learn, and to tailor the findings in a more practical, useful way that teachers can immediately employ in their instructional practices. Full of detailed suggestions for research-based instructional activities, the book is designed to help teachers meet challenges and produce understanding, fluency, and problem solving among their students.
Mathematics Learning in Early Childhood: Paths toward Excellence and Equity (National Research Council, 2009). The result of a comprehensive review of the research on mathematics learning in early childhood, this publication identifies critical areas for early mathematics study that will enable all students to reach their potential in mathematics. The research reported suggests that improvements in early childhood mathematics education will also particularly support those students at risk of falling behind in mathematics by providing them the strong foundations they need for future success.
In order to attain a rigorous level of learning and understanding of mathematics demanded for 21st-century success, students require a deep extended learning period followed by periodic review and practice that forges memory of what they learned. Teachers often say, “My students just don’t remember what they learned last week!!!” But research shows that often many students did not actually learn the content last week, so of course they cannot remember what they did not learn.
There is an enormous amount of research literature establishing the importance of original learning on retention/forgetting and on how best to structure review once original learning has occurred (see, for example, Zechmeister and Nyberg, 1982, for an overview). Many research studies have contrasted “massed practice” and “distributed practice,” with distributed practice generally found to be better than massed practice for retention (e.g., Underwood, 1961; Cepeda et al., 2009). Math Expressions uses distributed practice in the Remembering pages, with practice closer together just after learning and then becoming spaced farther apart (Cepeda et al., 2006). This research about practice after original learning does not apply to the phase of initial learning of content, which needs to be extended and deep and not spiraled for complex math content.
In Math Expressions the phases of initial learning and later practicing to remember are clearly separate, and both are emphasized. Students spend extended time learning and discussing concepts in class, and they do homework about these concepts to deepen the original learning. Then after the unit is over, that content appears on the Remembering pages on and off throughout the year. Both the Unit Test and the Remembering pages allow the teacher to identify students who need additional focused learning time on particular content. This ideally comes outside of class right after the Unit Test.
The authors of Adding It Up, the National Research Council’s 2001 publication on children’s mathematical learning, define productive disposition as “the tendency to see sense in mathematics, to perceive it as both useful and worthwhile, to believe that steady effort in learning mathematics pays off, and to see oneself as an effective learner and doer of mathematics” (p.131). The sections of this report that follow describe research on conceptual understanding, procedural fluency, application, strategic competence, mathematical practices, and problem solving, and show how the research in these areas connects to the Math Expressions program. But students’ learning and developing skill in these areas is dependent on their belief that math is understandable and that, with effort, they are capable of learning math. This kind of a productive disposition is an important factor in students’ success.
How is a productive disposition formed? Students develop a productive disposition as they engage in well-planned, purposeful learning activities. “Developing a productive disposition requires frequent opportunities to make sense of mathematics, to recognize the benefits of perseverance, and to experience the rewards of sense making in mathematics” (National Research Council, 2001, p.131). Many aspects of the Math Expressions program support the crucial building of a productive disposition. The years of classroom research that underlie Math Expressions established learning paths of supports and student strategies. These supports and strategies can move students from their initial knowledge to understanding of and fluency with formal mathematical methods and notation. Math Expressions fosters a helping community within the classroom. It sets high-level mathematical goals for all students and concentrates on prerequisite competencies to bring all students to mastery.
For all major, grade-level topics, Math Expressions starts at each student’s level and continually elicits their thinking, provides visual and linguistic supports to move them to understanding, and ends with extended fluency practice, while continuing the emphasis on understanding and explaining with Math Talk. The curriculum is organized into ambitious, core, grade-level topics, with structured supports to bring students to a higher mathematical level. Daily Quick Practice activities in the classroom provide opportunity and structure for developing student leadership and self-regulation. Together and individually, students build prerequisite skills and bring new skills to fluency. Eventually, all students take on leadership roles within the Quick Practice activities. Acting as a leader develops confidence in every student, regardless of achievement level. Through these roles, students gradually assume more responsibility for learning.
And this is a key aspect of Math Expressions: Everyone, including the teacher, is both a teacher and a learner. Students learn to be helpful, contributing members of a teaching-learning math community as they work and talk together. In such a learning environment, students are made to feel safe, trusted, and validated. In such classrooms, competence and confidence develop hand in hand, and all take the learning path together to mathematical proficiency.
“Effective teaching of mathematics establishes clear goals for the mathematics that students are learning, situates goals within learning progressions, and uses the goals to guide instructional decisions” (NCTM, 2014, p.3).
Research in mathematics education among top-performing nations indicates that a greater focus on less content leads to greater mastery (National Mathematics Advisory Panel, 2008). Consequently, organizations such as the National Council of Teachers of Mathematics (2014) strongly recommend curricula that develop important mathematics along coherent learning progressions. “A robust curriculum is more than a collection of activities; instead, it is a coherent sequencing of core mathematical ideas that are well articulated across the grades” (p.4).
A coherent math curriculum is sequentially ordered to best reflect the hierarchical and logical structures of mathematics (Schmidt, Wang, & McKnight, 2005). Because math learning occurs sequentially, builds on previous learning, and develops in sophistication, mathematics education must address the idea of progression that helps students see a curriculum as a broader learning process with defined goals for learning (Marzano, 2009). Learning progressions are carefully sequenced sets of sub-skills and bodies of enabling knowledge that students must master to reach more distant curricular goals (Popham, 2006).
Identifying and clarifying expectations for learning and understanding in a mathematics classroom is an essential component to mathematical success (Wiliam, 2011), and establishing clear, explicit learning goals is the first step in building a unit of instruction; these goals set the stage for all instruction to come and generate motivation for learning (Hiebert, et al., 2007; Marzano, 2009). Goals within mathematics learning progressions provide teachers with opportunity to examine and monitor student progress and needs in order to adjust instruction as necessary (Charles, 2005; Clements & Sarama, 2004; Sztajn, Confrey, Wilson, & Edgington, 2012). Students in classrooms where learning goals are clearly articulated perform at higher levels than do students who are unaware of the expectations (Hattie, 2009) and are more aware of their own thinking and learning (Clarke, Timperley, & Hattie, 2004; Zimmerman, 2001).
Math Expressions reflects this strong attention to focus and coherence. The program introduces content in carefully coherent, focused progressions that align to what researchers know about effective sequencing in math instruction.
In 2008, the National Mathematics Advisory Panel reported its findings on its review of scientific evidence to advise on improvements in mathematics education of the nation’s children. A major recommendation was curriculum overhaul at the elementary and middle school levels to establish a focused, coherent progression of mathematics learning, with emphasis on proficiency with key topics. The panel further stressed that any approach to mathematics that continually revisits topics year after year without closure should be avoided. In a comparison of mathematics education in the United States to that of other countries, the National Research Council (2001) found the teaching in American math classrooms lacking in depth and rigor. Reviews of the mathematics curriculum in top-performing countries find that they “present fewer topics at each grade level but in greater depth” (National Mathematics Advisory Panel, 2008, p.20).
The National Council of Teachers of Mathematics (NCTM)’s 2014 publication Principles to Actions: Ensuring Mathematical Success for All outlines best practices for mathematics instruction. These principles are based on more than a decade of research and experience and continue to be a driving force behind a high-quality mathematics education for all students. Pointing out that “piecemeal efforts aimed at narrow learning goals have failed to improve U.S. students’ learning” (p.12), NCTMÒ calls for mathematics teaching that develops understanding through coherent curricula that sequence core mathematical ideas into learning progressions.
“[A] well-articulated curriculum gives teachers guidance regarding important ideas or major themes, which receive special attention at different points in time,” as, specifically, “…it must be coherent, focused on important mathematics, and well-articulated across the grades” (p.14).
Effective mathematics instruction is characterized by clear goals for learning that are structured within a framework of learning progressions and used to guide instructional decisions (NCTM, 2014).
Focused, Goal-Driven Instruction
As noted by Marzano in Designing and Teaching Learning Goals and Objectives (2009), identifying goals is the first step in building a unit of instruction. Identifying and clarifying what students are expected to learn and understand in a mathematics classroom is an essential component of success (Wiliam, 2011). Teachers and students benefit from establishing a shared foundation of what is being learned and why it is important to learn. “Formulating clear, explicit learning goals sets the stage for everything else” (Hiebert et al., 2007, p.57). Specific goals articulate a clear path for behavior and desired performance and serve as motivation for learning (Marzano, 2009). Setting clear goals and expectations increases motivation by encouraging student involvement in and responsibility for their own learning (Bransford, Brown, & Cocking, 2000). Research also shows that setting and sharing learning goals with students has a positive impact on their learning. Hattie (2012) found that students in classrooms where learning goals are clearly articulated perform at higher levels than students who are unaware of the expectations. When expectations are discussed with students, they are able to find value in their work and understand the greater purpose of what they are learning (Black & Wiliam, 1998; Marzano, 2009). Establishing goals allows students to focus on the expectation that is set and become more aware of their own thinking and learning (Clarke, Timperley, & Hattie, 2004; Zimmerman, 2001).
Meaningful Progression across Grade Levels
A coherent math curriculum is sequenced within and across grade levels in a way that best reflects the hierarchical and logical structures of mathematics (Schmidt, Wang, & McKnight, 2005). Learning progressions are a “carefully sequenced set of building blocks that students must master en route to a more distant curricular aim. The building blocks consist of subskills and bodies of enabling knowledge” (Popham, 2006, p.83). It is important that educators see a connected progression, not a static picture (Marzano, 2013). And because math learning occurs sequentially, building on previous learning and developing in sophistication, part of a discussion of content in mathematics must address the idea of sequence or progression. “To help students see the curriculum not as isolated bits of information, but as a learning process, learning goals and scales can show them they are building on previous knowledge” (Marzano, 2013, online). By making connections, students and teachers are able to see a bigger picture— one that shows how what they learned before relates to what they are learning now and to what they will learn next. Strong learning progressions build deep content knowledge and build the complexity of student skills over time.
In comparing math performance among students in the United States with the performance of students in higher-achieving countries, one repeated conclusion has been that “successful countries tend to select a few critical topics for each grade and then devote enough time to developing each topic for students to master it. Rather than returning to the same topics the following year, they select new, more advanced topics and develop those in depth” (National Research Council, 2001, p.37). In contrast, as stated previously, the American curriculum has often been more diffuse and over-crowded in its content coverage, and lacking the focus of more effective curricula.
The most effective instructional programs will build on children’s intuitive mathematical thinking and use that initial understanding to help children learn to solve problems, employ strategies, and engage in mathematical thinking (Carpenter, Fennema, Franke, Levi, & Empson, 2015). In terms of content, research suggests that for the youngest children, developing a thorough understanding of number and of geometry and spatial measurement is developmentally appropriate and especially crucial to supporting later study (Cross, Woods, & Schweingruber, 2009). According to Cross and colleagues, “Developing an understanding of number, operations, and how to represent them is one of the major mathematical tasks for children during the early years” (p.22). In addition, “Geometry and measurement provide additional, powerful systems for describing, representing, and understanding the world” (p.35).
For young students, a deep understanding of number is essential. Students must develop an understanding of number that “includes understanding concepts of quantity and relative quantity, facility with counting, and the ability to carry out simple operations” (Cross et al., 2009, p.22).
Also critical is an early understanding of geometry and measurement: “Geometry is the study of shapes and space, including two-dimensional (2-D) and three-dimensional (3-D) space. Measurement is about determining the size of shapes, objects, regions, quantities of stuff, or quantifying other attributes. Through their study of geometry and measurement, children can begin to develop ways to mentally structure the spaces and objects around them. In addition, these provide a context for children to further develop their ability to reason mathematically” (Cross et al., 2009, p.35).
In the elementary grades, students must develop understanding and use of the big ideas in mathematics. “Mathematics learning in early childhood requires children to use several specific mathematical reasoning processes, also known as ‘big ideas,’ across domains. These big ideas are overarching concepts that connect multiple concepts, procedures, or problems within or across domains or topics and are a particularly important aspect of the process of forming connections” (Cross et al., 2009, p.44).
The “big ideas” are key concepts and procedures that can be used to teach varied math skills and processes. “Big ideas” in mathematics include concepts and procedures such as the following:
- Place Value to One Million
- Addition with Multi-Digit Numbers
- Subtraction with Multi-Digit Numbers
Because these “big ideas” relate and connect to many other mathematical ideas, they help students develop a deep understanding of mathematics as a set of ideas—not isolated facts or disconnected skills (Charles, 2005).
Worth noting is that not everything taught in mathematics fits neatly into a conceptual progression. While there is a temptation “to want to discover universal progressions in learning that are driven by deep changes in conceptual structure ...there are parts of mathematics learning that, although important and complex, are driven by more incremental mechanisms” (Sherin & Fuson, 2005, p.385). This does not suggest, however, that isolated, repeated practice is effective, but rather than there are some mathematical skills which may be best developed with practice in the context of a “meaningful examination of patterns and strategies” (p. 386).
This alignment between standards, curriculum, instruction, and assessments is critical. Researchers looking at effective educational practices identified nine characteristics of high-performing schools and reported that several of these relate to standards and standards alignment. High-performing schools have a clear, shared focus; high standards and expectations for all; and curriculum, instruction, and assessments aligned to the standards (Shannon & Bylsma, 2003).
Built upon the research base shared with the National Research Council as described above, and infused with program author Dr. Karen Fuson’s deep knowledge of effective, research-based practices, content and models in Math Expressions connect and build across the grade levels to provide a clear, meaningful, aligned progression of teaching and learning mathematics.
Focused and Cohesive Program Content
In Math Expressions, ambitious, grade-level topics and big ideas for essential learning of priority core concepts are the focus of the curriculum at each grade level. These foster students’ deep understanding of major mathematical ideas and mastery of content ahead of progression.
Within the Teacher’s Edition, a statement of what students will learn in each lesson promotes objective-based planning, teaching, and assessment. Every activity within a lesson has a specific purpose in the progression of mathematics understanding, and the Teacher’s Edition cites valuable math background for each lesson.
Effective Learning Progressions as the Program’s Foundation
Math Expressions is organized into meaningful progressions that connect key topics between the grade levels. The curriculum reflects research on students’ natural stages of learning when mastering concepts such as computation and problem-solving strategies. These learning stages informed the order of concepts, the sequence of units, and positioning of topics in Math Expressions. The program’s sequence and progression of teaching and learning experiences is also thoughtfully built upon a body of research on how young learners in mathematics develop number concepts and understanding of and skill with single- and multi-digit addition, subtraction, multiplication, and division; solving word problems; and fractions, ratio, and proportion.
The Math Expressions Teacher’s Edition allows teachers to structure learning paths for students based on their own progressions of learning, with a focus on understanding and fluency.
Teachers are guided throughout the program with Math Background, which makes Learning Progressions clear and interconnected within and across units and relates lessons in each unit to the Learning Progressions to show how the standards, and aligned lessons, build within and across grades.
“Effective teaching of mathematics consistently provides students, individually and collectively, with opportunities and supports to engage in productive struggle as they grapple with mathematical ideas and relationships” (NCTM, 2014, p.3).
Equitable access to a rigorous, quality mathematics curriculum and high expectations for all students are necessary for closing persistent achievement gaps within the United States and between the United States and other nations as well as for students to meet 21st-century demands for complex problem solving (NCTM, 2009, 2014).
Students succeed within a rigorous math curriculum via effective instruction, a range of approaches and resources, and differentiated supports. Additionally, some widely and persistently held beliefs about mathematical learning must change: Educators and students both must adopt growth mindsets and positive views on the productive struggle that is inherent to the process of learning math with understanding, as perseverance through challenging concepts and complex problems yields numerous benefits to students and boosts achievement (Boaler, 2011 & 2016; Dweck, 2006 & 2008; Hiebert & Grouws, 2007; NCTM, 2014; Pascale, 2015).
Rigor in a set of curricular expectations is essential to students succeeding at high levels, but only if placed on a foundation of deep understanding and strong skills and fluency. While some have suggested that a solution to the problem of low student mathematical skills is to reduce the focus on computation and “simpler” math skills, research suggests that students’ performance on items of low and high difficulty correlate highly—suggesting that students’ “mathematical abilities to solve problems at different levels of mathematics rigor are complementary” (Ginsburg, Cooke, Leinwand, Noell, & Pollock, 2005, p.v). Deep understanding cannot be achieved without fluency and fluency cannot be reached without understanding.
Rigor in the mathematics classroom also requires that teachers attend to three components essential to the learning of mathematics: conceptual understanding, fluency, and application (Gaddy, Harmon, Barlow, Milligan, & Huang, 2014; NCTM, 2014). Tasks that consistently encourage high-level student thinking and reasoning versus those that are routinely procedural yield the greatest learning; and tasks of higher cognitive demand are necessary when promoting reasoning and problem solving in the mathematics classroom (Boaler & Staples, 2008; Miri, David, & Uri, 2007; NCTM, 2014; Stein & Lane, 1996).
Math Expressions provides a rigorous curriculum that develops conceptual understanding and fluency and encourages application. Students are adequately supported while being challenged by high-level thinking and complex problem solving.
Never before has the workplace demanded such complex levels of mathematical thinking and problem solving (NCTM, 2009). To keep pace with a rapidly changing world, our students need to be prepared for a future in mathematics.
Although the United States has seen some increases in mathematics achievement, our students still score below average on international tests of mathematical knowledge and skills (Loveless, 2011). Among 34 countries participating in the 2012 Program for International Student Assessment (PISA) of 15-year-olds, the United States ranked 26th in mathematics—and between 2003 and 2012, the U.S. mean score on PISA declined while many other countries witnessed gains (NCTM, 2014). The picture is similar for national statistics. We have made some gains, but nearly two-thirds of our nation’s eighth graders do not meet current mathematics standards (National Center for Education Statistics, 2015).
The difference in average NAEP scores between white and black and white and Hispanic 9- and 13-year-olds narrowed somewhat between 1973 and 2012; however, the divide persists between 17 and 28 points, and the average NAEP score for 17-year-olds has remained relatively flat since 1973 (NCTM, 2014). Further, less than half of our college-bound students are prepared for post-secondary education and beyond (College Board, 2011). Clearly, we need to reevaluate, redesign, and reinvent our approach to mathematics teaching and learning to address our continued challenges. Rigor in instruction and expectations is key.
An analysis of TIMSS and PISA results led researchers to conclude that students need to focus each year on developing the skills that will allow them to perform well in low- and high-level problem-solving situations, on both low- and high-rigor mathematical content, as the United States is performing below average across such levels of difficulty. For all countries there is significant correlation on scores of low and high rigor, whether measured by skills or difficulty (Ginsburg et al., 2005).
Persistent and unacceptable gaps narrow and ultimately disappear when all students have access to rigorous, high-quality mathematics, taught by teachers who not only understand mathematics but also understand and appreciate learners’ social and cultural contexts in meaningful ways (NCTM, 2014, p.65).
Equitable Access to Rigorous Mathematics Curriculum for All Students
The National Council of Teachers of Mathematics (2014) encourages educators to set for all students clear, explicit learning goals that relate and build toward rigorous standards for learning that align with the current classroom curriculum and student needs. When differences in ability, background, and interest arise within and across schools—as they always will—access to a rigorous curriculum for all students is far more likely to raise achievement than policies that relegate students who have traditionally underperformed to dead-end tracks with an unchallenging curriculum. Students overcome obstacles to success within a rigorous math curriculum via effective instruction, a range of approaches and resources, and differentiated supports that boost and supplement learning and provide additional time if needed.
Attending to access and equity means recognizing that inequitable learning opportunities can exist in any setting, diverse or homogenous, whenever only some, but not all, teachers implement rigorous curricula. Abundant research has documented the significant outcomes that are possible when schools and teachers systematically address obstacles to success in mathematics for students from historically underserved populations (Boaler 1998, 2006; Boaler & Staples 2008). The question is not whether all students can succeed in mathematics but whether the adults organizing mathematics learning opportunities can alter traditional beliefs and practices to promote success for all (NCTM, 2014, p.60–61).
Growth Mindset
“To ensure that all students have access to an equitable mathematics program, educators need to identify, acknowledge, and discuss the mindsets and beliefs that they have about students’ abilities” (NCTM, 2014, p.64). A concept pioneered by psychologist Carol Dweck, growth mindset is a belief that a person’s intelligence, competence, and talents can be developed through dedicated efforts and hard work.
A growth mindset within mathematics emphasizes teaching and learning as processes that cultivate mathematical abilities; stresses that success and learning are reflections of effort and not intelligence alone; and promotes a belief that all students are capable of participating and achieving in mathematics(Boaler, 2011, 2016; Dweck 2006, 2008; NCTM, 2014). Mindsets have contributed to persistent negative perceptions within mathematics education specifically (Boaler, 2011, 2016; Dweck, 2008). Society has traditionally valued the math learner who can memorize well and calculate fast, rather than others who possess equal potential but may be deeper, slower, and possibly more creative (Boaler, 2016).
Teachers should promote and display a growth mindset by valuing all students’ thinking and efforts while relying on pedagogical practices such as differentiated tasks, mixed-ability groupings, and praise for students’ contributions and perseverance within their mathematical learning (Boaler, 2011, 2016; Dweck 2006, 2008; NCTM, 2014). Lasting change can be generated through daily activities that reinforce the importance of growth mindset. Schools and classrooms that reinforce growth mindset messaging make learning enjoyable and place the focus on that learning rather than on students’ performance (Yeager, Paunesku, Walton, & Dweck, 2013). Fostering and supporting growth mindsets can make an enormous positive impact on achievement: setting and supporting rigorous expectations and a genuine belief that student effort and effective instruction outweigh “smarts” and circumstances increase students’ opportunities to learn (Boaler, 2011, 2016; NCTM, 2014). Ultimately, problem solving in the mathematics classroom encourages students to see that their actions can lead to intellectual growth, and this “focus on the potential of students to develop their intellectual capacity provides a host of motivational benefits” (Blackwell, Trzesniewski, & Dweck, 2007, p.260).
Productive Struggle
Research has demonstrated that struggling to make sense of mathematics is a necessary process in the learning of mathematics with understanding (Hiebert & Grouws, 2007; Warshauwer, 2015). Teachers who guide students through such productive struggle are supporting the development of student learning and understanding. When carefully supported toward a resolution and given appropriate time to make sense of mathematics and to figure something out that is not immediately apparent, students can engage in efforts that advance their thinking and play an important role in deepening their understanding. Such a process provides students with the opportunity to practice and engage (Goldenberg et al., 2015; Pascale, 2015). This complex process of perseverance with mathematical problems and ideas encourages students to think about their own thinking and to discover that learning can happen without rushing to simply find the correct answer (Hiebert & Grouws, 2007). It has also been found that students given time to make mistakes and persist through their struggles ultimately show greater understanding on post-test measures than their counterparts (Kapur, 2010).
Teachers need to carefully select tasks that require students to struggle and must also provide reassurance and instructional support that students need without diminishing the cognitive demand of the task or giving students too much help or direct answers. Students need sufficient time not only to solve difficult mathematical problems that require them to choose and grapple with mathematical approaches, but also to develop curiosity and stamina (Goldenberg et al., 2015). As Math Expressions author Karen Fuson and colleagues found, engaging in problem solving teaches students how to employ strategies to solve problems—which helps them when they are faced with future problem situations (Hiebert et al., 1996). Finally, teachers must create a classroom culture that demonstrates how struggle is a natural part of the learning process (Star, 2005) and allows students to see the benefits of persevering (Hiebert & Grouws, 2007).
The kinds of questions teachers ask and the kinds of support teachers offer are critical, as they either facilitate or undermine the productive efforts of students’ struggles and determine whether students view struggle as a positive endeavor or the source of difficulty and frustration (Warshauer, 2015). Timing of support also plays a vital role. When scaffolding is given to students before they have the opportunity to make sense of a challenging task independently, without teacher assistance, they are inhibited from developing productive perseverance. “All too often, so much support is provided through the initial scaffolding that the cognitive demand of the task is significantly decreased” (Boston & Wilhelm, 2015). If this sort of scaffolding is provided up front for students who struggle, then these same students are denied access to cognitively demanding tasks. When access is denied, equity becomes an issue” (Dixon, 2018).
Cognitive Demand
Rigor in the mathematics classroom also entails paying equitable, balanced attention to conceptual understanding, fluency, and application, three components essential to the effective teaching and learning of mathematics (Gaddy, et al., 2014; NCTM, 2014). Student learning is greatest in classrooms where the tasks consistently encourage high-level student thinking and reasoning and least in classrooms where the tasks are routinely procedural (Boaler & Staples, 2008; Stein & Lane, 1996).
Tasks requiring a high level of cognitive demand are necessary when promoting reasoning and problem solving in the mathematics classroom. In a study that compared students exposed to teaching strategies that promoted higher-order thinking with those who were taught more traditionally, researchers found that experimental group students outperformed control group students, showing significant improvement in their critical thinking skills; “Our findings suggest that if teachers purposefully and persistently practice higher order thinking strategies for example dealing in class with real-world problems, encouraging open-ended class discussions, and fostering inquiry-oriented experiments, there is a good chance for a consequent development of critical thinking capabilities” (Miri, et al., 2007, p.353).
Conceptual understanding describes one’s “integrated and functional grasp of mathematical ideas. Students with conceptual understanding know more than isolated facts and methods. They understand why a mathematical idea is important and the kinds of contexts in which it is useful. They have organized their knowledge into a coherent whole, which enables them to learn new ideas by connecting those ideas to what they already know” (National Research Council, 2001, p.118). According to Cross and colleagues (2009), key here is both that students acquire knowledge and that they purposefully “access and apply this knowledge in new situations” (p.244).
According to the research findings presented in Adding It Up: Helping Children Learn Mathematics (NRC, 2001), conceptual understanding benefits students because it allows them to make connections between current knowledge and new topics and thereby learn more quickly. Students can avoid critical errors because they can readily assess the reasonableness of solutions.
In their study of mathematics learning in early childhood, Cross and colleagues (2009) concluded that to effectively foster students’ conceptual understanding, teachers must include four key elements or opportunities within their teaching and learning activities: analyzing and reasoning; creating; integrating; and making real-world connection.
In a study in which they compared students using a traditional control program with modified programs that employed worked examples, Booth, Lange, Koedinger, and Newton (2013) found that explaining worked examples—both correct and incorrect—during practice fostered deeper conceptual understanding.
Studying young children from backgrounds of poverty, Fuson and colleagues (with Clements & Sarama, 2015; & Smith, 2015) report that students are able to demonstrate high levels of conceptual understanding when they receive instruction designed to provide opportunities to learn concepts and that employed strategies that included math drawings and intensive and conceptual learning experiences with visual supports.
Procedural Fluency
In its position statement on procedural fluency, the National Council of Teachers of Mathematics identifies procedural fluency as the ability to apply procedures accurately, efficiently, and flexibly; to transfer procedures to different problems and contexts; to build or modify procedures from other procedures; and to recognize when one strategy or procedure is more appropriate to apply than another and as a critical component of mathematical proficiency.
All students need to have a deep and flexible knowledge of a variety of procedures, along with an ability to make critical judgments about which procedures or strategies are appropriate for use in particular situations for best success in the mathematics classroom (NRC, 2001, 2005, 2012; Star, 2005). The goal for students developing procedural fluency is that over time they will possess a body of known facts and generalizable methods that will allow them to efficiently and accurately solve varied problems.
A tension has existed historically in the United States between understanding and fluency. In outlining a framework to describe effective teaching and learning in mathematics, Fuson (2009) describes this tension in more detail. She states that some educators’ misinterpretations of Piaget led to a greater emphasis on children’s interactions with objects and activities—an emphasis on “understanding at the expense of fluency,” which might have been “termed by its opponents as mathematical learning without teaching” (p.345).In contrast to this approach is mathematical teaching without learning, in which rote practice and worksheets without attention to meaning-making are the focus. Fuson suggests that rather than having to choose one of these extremes, there is a balanced learning-teaching option, in between child-invented methods with too little structure and teachers’ efficient methods with too much structure. In the balanced approach, teachers can structure learning paths for students based on their own progressions of learning, with a focus on both understanding and fluency.
To achieve proficiency, students need instruction that recognizes the relationship between procedural fluency and conceptual understanding. Specifically, “Effective teaching of mathematics builds fluency with procedures on a foundation of conceptual understanding so that students, over time, become skillful in using procedures flexibly as they solve contextual and mathematical problems” (NCTM, 2014, p.42). Effective mathematics instruction cannot have one without the other as “procedural knowledge and conceptual understandings must be closely linked” (NRC, 2005, p.232). Rittle-Johnson and Alibali (1999) and Rittle-Johnson, Siegler, and Alibali (2001) found, too, that concepts and procedures develop iteratively—and gains in one area lead to gains in the other.
Research by Hiebert suggests that once students have memorized and practiced procedures that they do not understand, they have less motivation to understand their meaning or the reasoning behind them (Hiebert, 1999). When learning is not meaningful and is disconnected from other knowledge, students have a more difficult time absorbing concepts. When students are able to connect procedures and concepts, their retention improves and they are better able to apply what they know in different situations (Fuson, Kalchman, & Bransford, 2005).
Practice is key to developing procedural fluency. Research suggests that to be effective, teachers should create opportunities for practice that are brief, engaging, purposeful, and distributed over time (Rohrer, 2009).Worked examples, rather than additional practice problems, have also been shown to be effective in helping students learn to solve problems faster, perhaps because these worked problems help reduce students’ cognitive loads and allow them to focus on the learning (Booth et al., 2013). Math Expressions uses worked examples in the classroom by having students solve and explain methods to their classmates during the frequent Math Talk parts of a lesson.
NCTM (2014, p.47) advises that teachers do the following to build procedural fluency from conceptual understanding:
- Providing students with opportunities to use their own reasoning strategies and methods for solving problems.
- Asking students to discuss and explain why the procedures that they are using work to solve particular problems.
- Connecting student-generated strategies and methods to more efficient procedures as appropriate.
A wide body of research (see, for example, Baroody, 2006; Fuson & Beckmann, 2012/2013; Fuson, et al., 2005; Fuson & Murata, 2007; Russell, 2000) suggests that to develop students’ fluency in procedures, teachers should do the following:
- Build on a foundation of conceptual understanding.
- Support students in looking for patterns.
- Allow students to flexibly choose among solution methods.
- Offer distributed opportunities for purposeful, meaningful practice (not rote, repeated practice).
The third of the essential components of rigor within the mathematics classroom is application, which draws on both conceptual understanding and procedural fluency (Gaddy et al., 2014). Application is the “why we learn math” piece. We learn math so we can use it in situations that require mathematical knowledge. Rigorous standards require application across K–12. But correctly applying mathematical knowledge depends on solid conceptual knowledge and procedural fluency. If students attempt to start solving real-world problems when they lack knowledge and fluency, problems are made unnecessarily, perhaps prohibitively, challenging. Yet at the same time, educators should not save all application for the end of learning progressions. Application can be motivational and interesting, and students at all levels need to connect the mathematics they are learning to the world around them (Alberti, 2013).
Application also depends on and develops two of the five aspects emphasized in Adding It Up (NRC, 2001): (1) strategic competence and (2) adaptive reasoning. When students build conceptual understanding and procedural fluency, they must extend their new knowledge and skill into application.
Within effective curricula, lessons incorporate contextual applications of mathematics as part of rich and rigorous problem-solving tasks that are essential for developing mathematical understanding (David & Greene, 2007; NCTM, 2014).
Math Expressions empowers teachers to differentiate instruction with an appropriate level of rigor for each student. Math Expressions helps students make sense of mathematics by developing a foundational approach that serves as a gateway to more complex thinking. Program resources provide both challenge and support that move students rapidly toward content knowledge, with fluency practice and applications that continue the emphasis on understanding and explanation.
Personal Math Trainer® Powered by Knewton™ provides an online assessment and personalized learning system for students.
This feature allows for customized assignments based on ongoing assessment with automatic scoring and real-time reporting. Teachers can utilize optional personal study plans for students, using intervention and enrichment Knewton Adaptive Modes.
Math Expressions makes math accessible to all learners. Every lesson includes intervention, on-level, and challenge differentiation to take math from concept to real-world application.
The program’s new Online Student Activity Book eBook includes interactive features, making instruction both more accessible and more rigorous for ALL students.
- Dynamic audio
- Answer prompts
- Drawing tool
- On-demand guided practice
- Links to lesson-level resources for expanded coverage
Math Expressions fosters the development of Growth Mindset through multiple features that are integrated within the program’s five core structures that also support conceptual understanding and fluency. Math Talk, Student Leaders, and Helping Community aid students in learning to be leaders and develop confidence in their abilities.
The Math Expressions Teacher’s Edition allows teachers to structure learning paths for students based on their own progressions of learning, with a focus on understanding and fluency. Students spend the majority of their time on the major work of the grade level.
Research notes, consistent lesson organization, and differentiated instruction are provided for each lesson.
Conceptual Understanding and Procedural Fluency in Math Expressions
Math Expressions systematically moves students through phases structured to build conceptual understanding, procedural fluency, and application.
The program includes a Fluency Plan for helping students achieve fluency at each grade, kindergarten through Grade 6. This plan provides targeted practice in the Student Editions, Teacher’s Editions, and Teacher’s Resource Books, as well as Fluency Checks in the Assessment Guide.
Phase 1: Guided Introducing
In Phase 1, teachers elicit and the class works with prior knowledge that students bring to a topic. Teachers and students discuss ideas and methods.
Phase 2: Learning Unfolding (Major Sense-Making Phase)
In Phase 2, teachers help students form conceptual networks and use methods that are desirable and accessible. Research-based solution methods are discussed and explained. Math drawings and other supports help students correctly relate concepts and symbols and explain their thinking. Erroneous methods are analyzed and repaired. Advantages and disadvantages of varied methods are discussed.
Phase 3: Kneading Knowledge
Teachers help students gain fluency with desired methods. Students may choose a method and can explain why it works. Some reflection and discussion continue to take place.
Phase 4: Maintaining Fluency and Relating to Later Topics
Teachers assist students in remembering by providing occasional problems and making explicit connections between new topics and prior knowledge.
In Math Expressions, specific features designed to help students avoid common errors help them address misconceptions head on and develop concepts correctly. For example, the Puzzled Penguin shows typical student errors—that students can then explain and teach correctly to Puzzled Penguin.
Additional tools that support students’ development of conceptual understanding include Math Mountains and Secret Code cards, which help students focus on the 10-ness of our number system as they learn to compose and decompose numbers and add, subtract, multiply, and divide to solve problems. These types of visual supports were developed through Dr. Fuson’s research for the Children’s Math Worlds (CMW) NSF-funded project.
Math Expressions includes specific instructional activities designed to build students’ conceptual understandings and address possible misconceptions.
Application in Math Expressions
The approach to application, the third element of rigor, in Math Expressions begins with students making their own representation of a problem using a math drawing or situation equation. As numbers get larger, students learn to represent problems with research-based diagrams.
Student application of their conceptual understanding and procedural fluency in problem-solving situations is supported by Math Talk, during which students talk about aspects of how they apply their knowledge to problem situations.
Students represent and solve all problem types for all quantities at the appropriate grade levels: single-digit numbers, multi-digit numbers, fractions, and decimal fractions. They also pose problems for classmates to solve at every grade level.
Math Expressions provides many pathways to mathematical tasks. The program starts at the student’s level and continually elicits thinking, provides visual and linguistic supports to move the student rapidly to understanding, and ends with extended fluency practice and application while continuing the emphasis on understanding and explaining.
For experience in solving more in-depth project-related problems Math Expressions includes an In-depth Inquiry-Based task card for each unit that focuses on a real-world situation. Each card requires students to use the concepts and skills they have learned to arrive at a solution. The In-depth Inquiry-Based Task cards are located in the online and print Math Activity Center.
“Competing in such a [complicated] world requires great adaptability to unexpected challenges. For that, workers need not only the skills for solving problems that we already know about but also the stamina and disposition to puzzle through totally unfamiliar problems for which we cannot now provide methods and procedures. The ability to solve new and unforeseen problems requires mastery not just of the results of mathematical thinking (the familiar facts and procedures) but of the ways that mathematically proficient individuals do that thinking. This is especially true as our economy increasingly depends on fields that require mathematics. Mathematical proficiency depends also on other mental habits that dispose one to characterize problems (and solutions) in precise ways, to subdivide and explore problems by posing new and related problems, and to ‘play’ (either concretely or with thought experiments) to gain experience and insights from which some regularity or structure might be derived” (Goldenberg, et al.; 5, p.1–2).
What is mathematics? By looking at the many interrelated skills and knowledge involved in learning and doing mathematics, it is clear that mathematics is not simply a body of content or topics to be learned. Mathematics also encompasses ways of thinking and mathematical approaches that are essential to learning and doing math.
Learning in mathematics requires students to engage in practices and take a problem-solving approach, making connections and using productive reasoning. Students of math must demonstrate persistence when initial methods or strategies do not generate solutions. Students who are successful in mathematics double check their solutions to ensure that they have found a reasonable solution to the problem. All of these mathematical approaches can be taught and developed through modeling, practice, and problem-solving opportunities.
In their seminal article written with support from an NSF grant, Cuoco, Goldenberg, and Mark (1996) proposed that “more important than specific mathematical results are the habits of mind used by the people who create those results...this includes learning to recognize when problems or statements that purpose to be mathematical are, in truth, still quite ill-posed or fuzzy; becoming comfortable with and skilled at bringing mathematical meaning to problems and statements through definition, systematization, abstraction, or logical connection making; and seeking and developing new ways of describing situations” (p.376). This suggestion—that a curriculum be organized around mathematical ways of thinking, or habits of mind—with its focus on the how of learning instead of the what, anticipates the expression of these practices throughout Math Expressions.
Math Expressions develops habits of mind, mathematical practices, and problem-solving approaches so that students are empowered to continue, in school and in life, with a questioning mind, making connections and approaching problems flexibly, thoughtfully, creatively, and persistently, with a goal of accuracy and clear communication of results. For example, teachers have reported that students voluntarily carry their high-level analyzing and explaining skills developed in Math Talk to non-math lessons.
Mathematical habits of mind reflect how mathematicians think about situations in automated, internalized ways that allow them to persist through complex problems. Such problem-solving proficiency requires mastery not just of facts and procedures—the results of mathematical thinking—but also the practices of such thought processes and their accompanying behaviors. Additionally, the need for mathematical thinking extends well beyond the mathematics classroom. Developing mathematical habits of mind is essential to mathematical proficiency, critical thought, college and career readiness, access to future opportunities, and productive participation in society (Goldenberg et al., 2015).
“If we really want to empower our students for life after school, we need to prepare them to be able to use, understand, control, modify, and make decisions about a class of technology that does not yet exist. That means we have to help them develop genuinely mathematical ways of thinking” (Cross et al., 2009, p.21).
Researchers have advocated for using mathematical habits of mind as a framework for approaching math instruction for several decades but the idea is timeless: Mathematics has always been about more than its products—facts, methods, formulas, etc.—as successful study within the field draws on cognitive practices such as strategies and behavioral dispositions such as perseverance to solve complex problems (Cuoco et al., 1996; Goldenberg et al., 2015).
Mathematical Practices
In developing the Principles and Standards for School Mathematics, the National Council of Teachers of Mathematics (2009) identified expectations for content as well as for process. Under its Process Standards, NCTM includes Problem Solving, Reasoning and Proof, Communication, Connections, and Representation.
In attempting to define the many aspects of mathematics learning and understanding, the National Research Council (2001) identified five strands of mathematical proficiency:
- Conceptual understanding—Comprehension of mathematical concepts, operations, and relations
- Procedural fluency—Skill in carrying out procedures flexibly, accurately, efficiently, and appropriately
- Strategic competence—Ability to formulate, represent, and solve mathematical problems
- Adaptive reasoning—Capacity for logical thought, reflection, explanation, and justification
- Productive disposition—Habitual inclination to see mathematics as sensible, useful, and worthwhile, coupled with a belief in diligence and one’s own efficacy (p.5).
The group concluded that “The integrated and balanced development of all five strands of mathematical proficiency (conceptual understanding, procedural fluency, strategic competence, adaptive reasoning, and productive disposition) should guide the teaching and learning of school mathematics” (National Research Council, 2001, p.11).
The tasks with which teachers engage students in learning and doing mathematics is one of the most important instructional decisions that teachers make (Lappan & Briars, 1995). Tasks that allow students to make connections based on what they know, explore real-world problems, and promote higher-level thinking are particularly effective. The goal is that students “problematize with the goal of understanding the situations and developing solution methods that make sense” (Hiebert et al., 1996, p.19).
Math Talk is an essential component of mathematical thinking (Cuoco et al., 1996). The frequent use of Math Talk explaining in Math Expressions lessons lifts the students to engage in mathematical habits of mind.
Solving problems in the mathematics classroom has numerous benefits for students because they:
- Integrate their conceptual understandings with procedural fluency
- Develop more positive views of their abilities to solve problems
- Demonstrate and build persistence
- View the discipline of mathematics more positively
Problem Solving
“Students immersed in classroom experiences that let them engage in learning mathematics concepts through problem solving, making and using abstractions, and developing and applying mathematical theories have greater opportunities for developing mathematical habits of mind” (Bryant, 2015).
While some may see a dichotomy between gaining knowledge and applying knowledge, problem solving is a bridge between the two; solving problems enables students to build understandings while applying skills and knowledge. As Hiebert and colleagues (1996) suggest, problematizing the subject links with the development of students’ understanding; “Treating mathematics as problematic is the most powerful and practical way to think about problem solving” (p.18).
Additionally, according to Levasseur and Cuoco (2009), “Mathematical habits of mind develop as a by-product of teaching mathematics through problem solving” (p.36)—that is, through teacher modeling and student reflection during problem solving in order to internalize the habits:
…the crucial element is that students be given the opportunity to develop mathematical understanding through problem solving. The problems should not all be difficult, but they should challenge students to think about, and make sense of, the problems and the mathematics that underlies them. Reflection on solution methods is also crucial. In short, classrooms in which mathematics is taught through problem solving as described in this volume are excellent settings for these habits of mind to develop. Teachers can facilitate students’ development of these habits by making the habits explicit and by encouraging their students to reflect on them when opportunities arise (Levasseur & Cuoco, 2009, p.34–35).
Effective instruction in problem-solving is often situated within a meaningful or real-world context and encourage students to make connections. These connections—among mathematical ideas, with other content areas, and in real-world contexts—are an essential part of mathematical thinking and learning. Making connections between new information and students’ existing knowledge—knowledge of other content areas and of the real world—has proved to be more effective than learning facts in isolation (Beane, 1997; Bransford, Brown, & Cocking, 1999; Caine & Caine, 1994; Kovalik, 1994). Further, connecting mathematics to science, social studies, and business topics can increase students’ understanding of and ability with mathematics (Russo, Hecht, Burghardt, Hacker, & Saxman, 2011). Students see the purpose and value of learning when they experience it in real-world contexts; “When instruction is anchored in the context of each learner’s world, students are more likely to take ownership for...their own learning” (Mid-Continent Research for Education and Learning [McREL], 2010, p.7). According to Fosnot and Dolk (2010), teaching with contextual problems can be effective for developing “children’s mathematical modeling of the real world” (p.24). Connecting to the tasks improves their perception of the content as interesting and beneficial, thereby increasing their motivation to learn (Czerniak, Weber, Sandmann, & Ahem, 1999). Students learn best when what they learn seems relevant. [Although worth noting is Hiebert et al.’s (1996) argument that these real-life contexts can be engaging but are “not the primary determinant for engagement” (p.18).]
Effectively problematizing mathematics entails asking students to think for themselves and to explain their thinking, while supported by their teacher, classmates, and math program; to struggle productively; and ultimately to apply their gained knowledge and strategies to new and more complex problems they encounter in the future (Hiebert et al., 1996). Because the author of Math Expressions, Karen Fuson, was one of the authors of that 1996 paper, she understands this view deeply and implements it in Math Expressions.
Effective scaffolds can be useful in a mathematics classroom focused on problem solving that fosters the development of mathematical habits of mind. As Hyde (2006) states, “Scaffolding does not necessarily make the problem easier, and the teacher does not do the work for students or show them how to do it. It enables the person to do it” (p.28). Williams (2008) found that “scaffolding tasks allowed students to work independently at appropriately challenging levels…and develop a sense of self-confidence in their mathematics knowledge and skills” (p.329). The research-based diagrams and math drawings used by students in Math Expressions lessons scaffold student thinking as they need it because they use these visual supports to scaffold their own thinking and explain to their classmates.
Mathematical Practices in Math Expressions
In Math Expressions, instructional approaches that foster mathematical habits of mind are integrated throughout the program.
Using objects, drawings, conceptual language, and real-world contexts, Math Expressions engages students in practices that build mathematical habits of mind.
Math Talk is a key feature and an important vehicle to promote discussion. Each lesson includes a complete description of the activity and what teachers should expect from students, as well as explanations, sample questions, and student/teacher dialogs for Math Talk.
Problem Solving in Math Expressions
Math Expressions takes a research-based problem-solving approach, in which students:
- Interpret the problem
- Solve the problem
- Represent the situation
- Check that the answer makes sense
Math Expressions guides students through the processes and strategies they need to solve problems. Break- Apart Drawings and Compare Bars are examples of tools employed in Math Expressions to help students translate the words in a word problem into accurate situation equations.
Math Expressions is designed to build students’ problem-solving ability and give them the opportunity to apply their conceptual understandings and procedural skills. There are several problem types included in the program, and Math Expressions also provides extensive experience with such problems, beginning in kindergarten.
Students have ample opportunities for problem solving throughout Math Expressions. Real-World Problem Solving is integrated throughout the lessons.
In multistep problems, students may need to find the answer to hidden questions needed to answer the question of the problem. Math Expressions guides students to see these hidden questions, even when they do not appear in the original problem.
The Teacher’s Edition offers additional guidance in how to help students “Make sense of problems and persevere in solving them.”
“Effective teaching is the non-negotiable core that ensures that all students learn mathematics at high levels. An excellent mathematics program requires effective teaching that engages students in meaningful learning through individual and collaborative experiences that promote their ability to make sense of mathematical ideas and reason mathematically” (NCTM, 2014, pp.4, 7).
Teaching matters. The approaches that teachers take in the classroom can support students in learning and reaching their highest potential. A wide body of research has shown the impact of teacher effectiveness on student learning and achievement (Goldhaber, 2002; Partnership for Learning, 2010). Chetty, Friedman, and Rockoff (2012) looked at the long-term impacts of teachers and found that those who added value to their students’ test scores also added life-long value to their students’ educational attainment and income earning. High-quality teachers use effective classroom practices (Wenglinsky, 2002). Research—in cognitive science, on classroom practices of master teachers, and on specific supports that help students learn—points to specific principles and methods of effective instruction (Rosenshine, 2012). Effective teachers engage students in deep learning. Teaching mathematics is not easy, but employing proven research approaches can help teachers ensure all students learn.
“Our examination of teaching focuses not just on what teachers do but also on the interactions among teachers and students around content. Rather than considering only the teacher and what the teacher does as a source of teaching and learning, we view the teaching and learning of mathematics as the product of interactions among the teacher, the students, and the mathematics.” (NRC, 2001, p.313).
A wide body of research in mathematics supports the use of visual representations or drawings, created by teachers and students, and the incorporation of communication and classroom discourse as effective approaches for teaching mathematics. Visual representations can also be physical models or concrete objects that are used for teaching and learning (manipulatives), though drawings/diagrams have many advantages and are used extensively in Math Expressions. Both of these research-based approaches are evidenced throughout Math Expressions, in various activities and program features.
Visual Representations
According to the National Academies Press publication Mathematics Learning in Early Childhood, “representing is central to mathematics” (Cross et al.). This understanding is widely held by researchers and educators (see also, Stylianou, 2011 and NCTM, 2000 & 2014). “Because of the abstract nature of mathematics, people have access to mathematical ideas only through the representations of those ideas” (National Research Council, 2001, p.94). Visual representations are integral to learning mathematics also because of the intangible and invisible nature of the subject (Bobis & Way, 2018).
“Representations should be treated as essential elements in supporting students’ understanding of mathematical concepts and relationships; in communicating mathematical approaches, arguments, and understandings to one’s self and to others; in recognizing connections among related mathematical concepts; and in applying mathematics to realistic problem situations through modeling” (NCTM, 2000, p.67). Essentially, representations can show what students know, help students explain what they know, and be the foundation for making connections and achieving a deeper understanding of mathematics.
At every level, teachers and learners of mathematics use pictures or diagrams to represent situations. In mathematics, representations are not only written numbers or equations, the representations we immediately think of as “mathematical.” In fact, representations may include images, simple drawings, graphs, and other ways to see and think about mathematical ideas. Math drawings are tools for modeling, sense-making, reasoning, explaining, structuring, and generalizing.
What these representations share is that they enable teachers to explain and learners to understand situations quantitatively or geometrically. Representations bolster intuition and understanding (Blatto-Vallee, Kelly, Gaustad, Porter, & Fonzi, 2007) and can help students communicate, reason, problem solve, connect, and learn (Hill, Sharma, Obyrne, & Airey, 2014). Representations “help to portray, clarify, or extend a mathematical idea by focusing on its essential features” (NCTM, 2000, p.206).
At the earliest grade levels, visual representations are particularly helpful in building students’ understanding of number and geometry. Visual representations can help clarify concepts of tens and ones in the number systems—concepts that are made less clear by the structure of the English language. For young students, these visual representations and drawings of tens and ones can support understanding (Fuson, 2009). In a study with students in Grade 2, teachers successfully taught students to use schematic drawings to solve three-digit addition and subtraction word problems, and students demonstrated competence in choosing and applying the appropriate solution strategy (Fuson & Willis, 1989). Including visuals in the classroom can be particularly supportive of English learners and at-risk students (Fuson, Atler, Roedel, & Zaccariello, 2009; Fuson, Smith, & Lo Cicero, 1997).
Manipulatives are visual representations, as well; the term is used to refer to those concrete materials— such as blocks, cubes, base-ten blocks, place value cards (Secret Code cards), fraction strips, and so on—that teachers employ to develop students’ mathematical understandings and skills. In addition to being manipulable and grounded in the concrete world, manipulatives also provide teachers and students with a visual point from which to have conversations about mathematical topics, concepts, and situations (Thompson & Lambdin, 1994). Research suggests that manipulatives can be effective in increasing students’ mathematical knowledge (Clements & McMillen, 1996; Clements & Sarama, 2007b), particularly when care is taken in how students interact with the manipulatives. While manipulatives can be a primary vehicle for constructing knowledge, students will not automatically draw the same conclusions that their teachers draw; they must be helped to see the connections among the object, symbol, language, and concept (Ball, 1992a, 1992b).
In a study of Grades 1 and 2 students using concrete manipulatives to learn symbolic multi-digit addition and subtraction procedures, Fuson (1986) found that “for many children who made procedural errors on delayed tests, the mental representation of the procedure with the physical embodiment was strong enough for them to use it to self-correct their symbolic procedure” (p.35). So, self-correction may be an additional benefit of manipulatives. This benefit also applies to the use of drawings.
Manipulatives are scaffolds for understanding mathematical concepts, notations, and vocabulary; they are a means and not an end (NRC, 2001). They need to be related to written methods to make those methods meaningful. After students master a concept using manipulatives and make the relationships with written methods, they can move to solving the task without the visual support (Grupe & Bray, 1999).
A recent study indicates that using visual representations has shown to improve student performance in general mathematics, prealgebra, word problems, and operations (Gersten et al.2009). When students sketch or organize their mathematical thinking, they are able to explore their understanding of concepts, procedures, and processes—and communicate mathematically (Arcavi, 2003; Stylianou & Silver, 2004). Having students then participate in discussions about their representations allows for meaningful learning (Fuson & Murata, 2007). Visual representations are especially beneficial to students who have special needs, struggle with learning, or are English learners, but they are necessary for all learners and teachers.
Communication
A wide body of research supports the important role of communication in the mathematics classroom. Two National Research Council reports—Adding It Up and How Students Learn—emphasize discussion as a way to increase students’ mathematical understanding. Discussions of cognitively challenging mathematical topics and ideas are a primary mechanism for promoting conceptual understanding (Michaels, O’Connor, & Resnick, 2008).
For younger children in the mathematics classroom, communication is also important in developing mathematical concepts and learning. As Cross and colleagues (2009) note, “The informal and formal representations and experiences need to be continually connected in a nurturing ‘math talk’ learning community, which provides opportunities for all children to talk about their mathematical thinking and produce and improve their use of mathematical and ordinary language” (p.43). In the Children’s Math World (CMW) studies, Fuson and colleagues conducted research on the crucial aspects of discussions and the best ways for teachers to transition to student-to-student discussion. One phrase used to describe a classroom in which communication and discussion are primary vehicles for learning is the “Math-Talk Learning Community.” Hufferd-Ackles, Fuson, and Sherin (2004, 2015) describe a Math-Talk Learning Community as one in which “individuals assist one another’s learning of mathematics by engaging in meaningful mathematics discourse” (p.81). In their research, they articulated the framework that enabled success for one teacher in an urban neighborhood in a class with English learners. They found that creation of a Math-Talk community requires teachers to move from the level of a traditional, teacher-directed classroom (Level 0 in their framework) to a classroom in which teachers coach and assist as students take leading roles (Level 3). To do so, students need to develop skills across the components of questioning, explaining mathematical thinking, identifying the source of mathematical ideas, taking responsibility for learning, and mathematical representations.
Discourse in the classroom connects to increased learning and achievement. Klibanoff and colleagues (2006) conducted a study of how the teachers’ use of language impacted students’ mathematical knowledge. To test this, the researchers transcribed teachers’ language use, and found that the frequency of teachers’ Math Talk correlated with students’ increased mathematical knowledge. A review of studies conducted by NCTM revealed that “the process of encouraging students to verbalize their thinking—by talking, writing, or drawing the steps they used in solving a problem—was consistently effective…Results of these students were quite impressive, with an average effect size of 0.98” (Gersten & Clarke, 2007, p.2). Hatano and Inagaki (1991) found that students who discussed and justified their solutions with peers demonstrated greater mathematical understanding than students who did not engage in such discussions. Leinwand and Fleischman (2004) reviewed research on effective math instruction and concluded that talking about math and explaining the rationale for solutions builds conceptual understanding.
Communication appears to help students persist in solving problems and to increase motivation and engagement. Research has also shown that learners are engaged in the learning process when they are asked to explain and reflect on their thinking processes (Good & Whang, 1999; Hettich, 1976; Surbeck,1994). Continuing to work with students by asking them to explain and justify how they solved problems helps maintain student engagement (NRC, 2001).
Teachers can engage in specific discourse practices to encourage students’ “math talk.” Asking “Why?” and “How do you know?” is one strategy that effective teachers use to encourage students to explain their thinking, solve problems, and share mathematical strategies and ideas with their peers (Clements & Sarama, 2007a, 2007b; Thomson, Rowe, Underwood, & Peck, 2005). Instructional practices—such as restating, prompting students, and engaging in whole-class discussion, small-group discussion, and paired conversations—have been shown to be effective in improving student understanding (Chapin, O’Connor, & Canavan Anderson, 2003).
To foster a Math-Talk Learning Community, teachers play an important role in engaging and involving students, managing discussions, and coaching students on productive, collaborative speaking and listening. First, teachers must model solutions and explanations. They must build listening skills, asking students to repeat in their own words. Teachers must demonstrate effective questions, asking for clarification and explanations. Only with these kinds of supports will students transition into effective student-on-student discussions.
To be effective, math discourse should:
- Build on students’ thinking
- Provide ample opportunities for students to share ideas
- Engage students in analyzing and comparing approaches
The three phases of the teaching framework described by Fuson and Murata (2007) and summarized above emphasize math discourse in phases 1 and 2 when conceptual understanding is being emphasized. Supports for such Math Talk are used throughout the Math Expressions program.
Visual Representations in Math Expressions
In Math Expressions, Math Drawings are a key part of learning. These drawings focus on the mathematical aspects of quantities or of a problem situation. In Math Expressions, both students and teachers use Math Drawings as tools for teaching and learning. These meaningful Math Drawings are central to lessons in Math Expressions and are used together with Math Talk as students explain their thinking and listen to the explanations of other students. The use of math drawings enables students to work at their own entering level but move forward to build intertwined understanding and fluency.
As a tool for creating Math Drawings, Math Expressions uses individual dry-erase MathBoards. These boards can be used by students for representing and solving problems. They then can be displayed to share with peers and discuss the visual representations of problems and solutions. For example, see the Research and Math Background section of Math Expressions at Grade 2, Unit 2, for examples of how students use the MathBoard and Secret Code cards as tools to solve problems.
All grades include activities involving use of the program’s MathBoards. Students use a MathBoard for recording their thinking, relating their drawings to math language, and justifying their thinking.
To make math concrete and meaningful to students, the activities in Math Expressions utilize visual representations, including manipulatives, for concept development. Student manipulatives include traditional ones, and unique research-based Math Expressions manipulatives like Secret Code cards (for place value) and Make a Ten and Product cards (for meaningful practice) that provide students with visual models to promote understanding and procedural fluency. The strong emphasis in Math Expressions on representation and discussion open up the world of mathematics to all learners. There are opportunities for students to draw and view representations, listen to classmates discuss solution strategies and solutions, and explain and discuss their own strategies and solutions.
The program also includes iTools, electronic manipulatives that correspond to those used in the Math Expressions program.
Personal Math Trainer also provides an opportunity for students to work in a digital platform.
Communication in Math Expressions
Math Expressions has at its heart the Math-Talk Learning Community. Within this student-centered community, discourse is the shared way of building understandings and promoting one another’s thinking and learning. The opening of the Math Expressions Teacher’s Edition includes background and professional learning for teachers about how to build a successful Math-Talk community.
In Math Expressions, each new topic begins with the teacher starting where students are and eliciting their thinking. As students continue with their study, they transition from the use of primitive solution methods to more formal methods. To reach the goal of fluent use of formal methods to solve mathematical problems, the program uses research-based approaches that have been shown to be effective and accessible to students. A focus on sense-making, structures, the use of drawing and representations, and the expectation that students will explain their choices and solutions contributes to student learning and progression.
In Math Expressions, the goal is for students to engage in student-to-student Math Talk. To engage students in this kind of talk, research demonstrates the effectiveness of asking students to
- Solve
- Explain
- Question
- Justify
As described above, the program employs individual Math Expressions dry-erase MathBoards. These boards can be used by students for representing and solving problems and then displayed to share with peers and explain the solution.
In Math Expressions, there are four key components of the Math-Talk Learning Community. Students and teachers work together, engaging in the kinds of roles and activities described in the table below. The classroom works mostly at Stages 2 and 3.

This kind of Math-Talk Learning Community represents a shift from a traditionally organized classroom, in which the teacher is at the front of the room, delivering information and asking questions with a focus on correctness, and students respond when asked for answers, to a more collaborative partnership for learning, in which students are engaged in an ongoing conversation for learning. Accuracy is just as important, but now accuracy can be judged by students using their understanding of concepts, methods, and problems instead of coming from the teacher without understanding.
A key structure of the Math-Talk Learning Community in Math Expressions is for students to Solve and Discuss. Selected students will go to the board, solve a problem, and then two or three of them explain their solutions to the whole group. Or, students can work in small groups where each student explains their method to the others in the group.
In Math Expressions, the teacher orchestrates collaborative instructional conversations focused on the mathematical thinking of classroom members. Together, students and the teacher use seven responsive means of assistance that facilitate learning and teaching by all (several may be used together).
Means of Assistance for Creating a Nurturing, Sense-Making, Math-Talk Community
- Engaging and involving
- Managing
- Coaching: modeling, cognitive restructuring and clarifying, instructing and explaining, questioning, feedback
The teacher supports the sense-making of all classroom members by using and assisting students to use and relate:
- Coherent mathematical situations
- Pedagogical supports
- Cultural mathematical symbols and language
An excellent mathematics program ensures that assessment is an integral part of instruction, provides evidence of proficiency with important mathematics content and practices, includes a variety of strategies and data sources, and informs feedback to students, instructional decisions, and program improvement (NCTM, 2014, p.89).
Assessment is an essential part of the effective instructional cycle (NCTM, 2000). An effective assessment system addresses the depth and breadth of standards and all areas of a curriculum with a variety of measures (Darling-Hammond, 2010).
Teachers rely on assessment data to provide diagnostic information on students’ readiness. Ongoing, formative, informal, and formal assessment data are essential for meeting the needs of all students, identifying when instruction has been successful and when additional support, intervention, or challenge opportunities are needed. Summative data provide essential benchmark data for results and future planning. As noted by numerous research studies, the regular use of assessment to monitor student progress can mitigate and prevent mathematical weaknesses and improve student learning (Clarke & Shinn, 2004; Fuchs, 2004; Hattie, 2012; Lembke & Foegen, 2005; NCTM, 2014; Popham, 2008; Skiba, Magnusson, Marston, & Erickson, 1986).
For students, too, assessment is key to learning. Research shows that the act of preparing for assessment and being assessed leads to greater learning. The feedback students receive from assessment helps them evaluate their strengths and weaknesses, and gauge their progress toward meeting learning goals; formative assessment has a positive effect on learning (Black & Wiliam 1998; Cotton, 1995; Hattie 2012; Jerald, 2001).
Effective assessment tools allow teachers to collect data about what is working—and what is not—so they can take precise, swift, and effective action in meeting the specific needs of students. In their research, Baker, Gersten, and Lee (2002) concluded that “providing teachers and students with information on how each student is performing seems to enhance…achievement consistently” (p.67).
Math Expressions offers a comprehensive assessment program, with tools provided for each stage (diagnostic, formative, summative) and in varied formats. Throughout, teachers have the information they need to effectively plan and modify instruction to support all students to high levels of learning.
A Comprehensive Assessment Program
Assessment refers to all activities undertaken by teachers—and by their students in assessing themselves—that provide information to be used as feedback to modify teaching and learning activities (Black & Wiliam, 1998). Well-designed assessment conducted regularly and used by teachers to alter and improve instruction can have tremendous impact on students’ learning (NRC, 2005). “We believe that assessment, whether externally mandated or developed by the teacher, should support the development of students’ mathematical proficiency. It needs to provide opportunities for students to learn rather than taking time away from their learning” (NRC, 2001, p.423).
“When viewed as a process that is indistinguishable from effective instruction, assessment serves as a means to achieve productive teaching and learning for all, rather than merely as the final stage in the traditional teach-learn-assess cycle” (NCTM, 2014, p.94).
Teachers must examine incorrect student responses to see if they “reveal specific student misunderstandings” (Popham, 2006, p.86). By analyzing student errors, teachers can determine which specific concepts, algorithms, or procedures need additional instruction (Ketterlin-Geller & Yovanoff, 2009).
In defining the elements of an effective student assessment system, Darling-Hammond (2010) said that such a system must “address the depth and breadth of standards as well as all areas of the curriculum, not just those that are easy to measure” (p.1).
Varied Assessment Types and Options
Assessing students in meaningful ways is important to getting an accurate picture of students’ progress and learning (Herman, Aschbacher, & Winters, 1992). For this reason, using varied items types and tasks may be the best way to get an accurate, complete reflection of student understanding; “Using multiple types of assessments provides more insight into students’ learning because students have more than one way to demonstrate their knowledge and skills” (McREL, 2010, p.44). Employing performance-based assessments can also help assess multiple dimensions of learning (Marzano, Pickering, & McTighe, 1993).
Similarly, by asking students to respond to open-ended questions verbally, researchers Gersten and Chard (2001) found that “encouraging students to verbalize their current understandings and providing feedback to the student increases learning.” Researchers comparing student performance on assessments that include open-ended written responses with performance on multiple-choice tests found that students who wrote responses retained information better than those who responded to multiple-choice items (Roediger & Karpicke, 2006; McDaniel, Roediger, & McDermott, 2007).
Multiple-choice items can play an important role in an assessment system as well. These are the item types commonly found on high-stakes assessments and online assessments. The National Mathematics Advisory Panel (2008) found that formative assessments based on items sampled from important state standards objectives resulted in “consistently positive and significant” effects on student achievement (p.47). In addition, the panel found multiple-choice items to be equally valuable in assessing students’ knowledge of mathematics (National Mathematics Advisory Panel, 2008).
Formative Assessment
Research indicates that student learning improves when formative assessment is an integral component of instruction (Hattie, 2009; NCTM, 2014; Popham, 2008).
The phrase “formative assessment” encompasses the wide variety of activities—formal and informal—that teachers employ throughout the learning process to gather this kind of instructional data to assess student understanding and to make and adapt instructional decisions. Formative assessment is not an end; it is a means to guide teaching and learning as it occurs (Shepard, 2000; Heritage, 2007). Formative assessment shifts assessment from being something “done to students; rather, it should also be done for students, to guide and enhance their learning” (NCTM, 2000, p.22). Effective teachers use formal tools (such as quizzes or homework assignments) and informal tools (such as discussion and observation) to regularly monitor student learning and check student progress (Cotton, 1995; Christenson, Ysseldyke, & Thurlow, 1989).
When the Committee on Defining Deeper Learning and 21st-Century Skills sought to identify the central instructional approaches needed to ensure that students achieve 21st-century competencies, the group identified formative assessment as one of these key elements (NRC, 2012). As reported in Education for Life and Work, curriculum designed and developed for 21st-century learning should use formative assessment to “(a) make learning goals clear to students; (b) continuously monitor, provide feedback, and respond to students’ learning progress; and (c) involve students in self- and peer assessment” (NRC, 2012, p.182).
An additional benefit of formative assessment is that it has been shown to be particularly helpful to lower-performing students. Gersten and Clarke (2007) concluded that “the use of ongoing formative assessment data invariably improved mathematics achievement of students with mathematics disability” (p.2). As a result, formative assessments can minimize achievement gaps while raising overall achievement (Black & Wiliam, 1998b).
To be effective, intentional teaching requires that teachers use formative assessment to determine where children are in relation to the learning goal and to provide the right kind and amount of support for them to continue to make progress (Cross et al., 2009, p.227).
Summative Assessment
Studying student responses as a group can also provide evidence of common misconceptions (NCTM, 2000). Summative assessment also plays a role in the classroom. Checking student learning periodically in a unit and at the end of a unit offers insight when used as a point of information for subsequent instruction, as noted by Carnegie Mellon’s (2015) Eberly Center Teaching Excellence and Educational Innovation. Summative assessments are also useful as accountability measures for grading and gauging student learning against a set of standards or expectations. Summative assessments provide evaluative information to teachers about the effectiveness of their instructional program. Classroom summative assessments also appear to have an impact on student motivation and have the potential to positively impact learning (Moss, 2013).
Performance-Based Assessment
Economic and job trends internationally and technology innovations have necessitated that schools shift from fact-oriented curricula to emphasizing flexible, creative, effective approaches to problem solving (Fadel, Honey, & Pasnik, 2007; The School Redesign Network at Stanford University, 2008). In such an environment, performance-based assessment offers a needed tool that aligns with both how students learn and with the curricular emphases in the school.
Research has established the benefits of performance-based assessment. A review of classroom assessment practices in an age of high-stakes testing led Schneider, Egan, and Julian (2013) to conclude that “the value of high quality performance tasks should not be diminished and should be encouraged as an important tool” (p.66).
Performance-based assessments are positive because they look like what we want students to do in the classroom (Fox, 2004) and, as a result, can inform classroom practice in positive ways. Performance tasks allow teachers to engage students in real-world activities; they “emulate the context or conditions in which the intended knowledge or skills are actually applied” (American Educational Research Association [AERA], American Psychological Association [APA], and National Council on Measurement in Education [NCME], 1999, p.137). They model “what is important to teach and … what is important to learn” (Lane, 2013, p.313).
In a standards-aligned system in which high-stakes assessments are a part of the landscape, different types of assessments are important. But the most fundamental aspects of assessment are those the classroom teacher does to guide teaching. Math Expressions supports these formative assessments for teaching various ways described below as well as supporting other types of assessments.
A Comprehensive Assessment Program in Math Expressions
Math Expressions provides a comprehensive assessment system, including:
- Diagnostic Tools
- Formative Assessment
- Summative Assessment
- Review Opportunities
Formative assessment is a crucial piece of effective instruction, and is embedded within Math Expressions.
As research shows, the frequent use of both formal and informal formative assessment is essential to effective, ongoing classroom instruction. Math Expressions provides many opportunities to regularly assess student understanding and make and adjust instructional decisions.
Formative Assessment Opportunities in Math Expressions
- Check Understanding appears at the end of each lesson in the Teacher’s Edition and Student Activity Book. This allows teachers to check students’ understanding of the math content taught in the lesson.
- Quick Quizzes follow each Big Idea of the unit and are located in the Student Activity Book. These quizzes allow teachers to check students’ understanding of the math content included in each Big Idea.
- Math Talk and Math Drawing opportunities are incorporated daily in the Teacher’s Edition. These opportunities for discussions allow teachers to see and hear the thought processes a student goes through when solving math problems. Teachers can intervene at the point of struggle, fix common errors, and remediate or accelerate learning for individuals or the whole class.
- Math Writing Prompts appear on the back of the leveled Activity Cards in the Math Activity Center. There are three leveled writing prompts that provide teachers an opportunity to check students’ understanding of the math content through written communication.
- Homework and Remembering pages provide the teacher with daily feedback on student understanding.
The program also offers an Assessment Guide at each grade level with comprehensive assessment tools and resources. While Math Expressions provides several tools and resources for ongoing formative assessment, perhaps as important are the daily insights gleaned by observation of students’ work in the Math Talk Community. The Math Talk Community, supported by the program throughout the year, provides valuable data for formative assessment to guide teaching.
Finally, to keep all students on the grade-level learning path, Math Expressions is designed to support flexibility in offering more time and support to in-class periodic interventions and out-of-class Tier 2 and Tier 3 follow-up interventions. Teachers can use the Mastery Learning Loop to provide these kinds of periodic, in-class interventions for students who need the additional support. The Mastery Learning Loop is implemented as a full class period at specific times within the Math Expressions program pacing. In the Mastery Learning Loop for a given unit, a differentiation day occurs after each Big Idea, and one or more such days occur at the end of each unit. In this way, the program helps teachers in ensuring that all students master the content they need to move ahead.
Varied Assessment Types and Options in Math Expressions
Throughout Math Expressions, multiple effective types of assessment appear in order to best allow students to demonstrate their knowledge and skills.
Students complete open-response items to show their work and their processes. They engage in performance assessments that allow them to integrate multiple skills and demonstrate knowledge and skill in a problem-solving situation. The program provides ample opportunities for teachers to observe students at work, and make formative assessment decisions as a result.
Item types that comprise new high-stakes assessments and online assessments are included within Math Expressions, both in print and through the Personal Math Trainer. Varied assessment types in Math Expressions include the following:

“Providing young children with extensive, high-quality early mathematics instruction can serve as a sound foundation for later learning in mathematics and contribute to addressing long-term systematic inequities in educational outcomes” (Cross, Woods, & Schweingruber, 2009, p.2).
Effective tools and strategies for differentiating instruction and offering intervention as needed is particularly crucial in today’s diverse classrooms. In a single classroom, students may have diverse cultures, speak different languages, and differ in their prior knowledge, readiness, skills, motivations, interests, and learning styles (Tomlinson, 2005). These differences are important because “Research has identified consistent, average differences in mathematics competence and performance depending on membership in a particular social group” (Cross et al., 2009, p.101). These differing needs must be effectively addressed. Teachers must help all students achieve because “All young Americans must learn to think mathematically, and...think mathematically to learn” (NRC, 2001, p.1).
As noted in Principles to Actions: Ensuring Mathematical Success for All from National Council of Teachers of Mathematics (2014, p.60):
Support for access and equity requires, but is not limited to, high expectations, access to high-quality mathematics curriculum and instruction, adequate time for students to learn, appropriate emphasis on differentiated processes that broaden students’ productive engagement with mathematics, and human and material resources. Equity in school mathematics outcomes is often conflated with equality of inputs. Providing all students the same curricular materials, the same methods of teaching, the same amount of instructional time, and the same school-based supports for learning is different from ensuring that all students, regardless of background characteristics, have the same likelihood of achieving meaningful outcomes (Gutiérrez, 2013).
To help all students learn to think mathematically, teachers must meet them where they are. As Vygotsky (1978) noted in his seminal research on learning, optimal learning takes place within students “zones of proximal development”—when teachers assess students’ current understanding and teach new concepts, skills, and strategies at an according level.
Math Expressions has a strong emphasis on differentiation for teaching all learners and on intervention in response to specific needs. The program’s emphasis on the visual (such as through Math Drawings) and the verbal (such as through Math Talk) provides a path to learning for all learners. Math Expressions uses the class learning path model and so initially does a great deal of differentiating in the whole class. These approaches are discussed further below. Math Expressions addresses both of the quotes that began this section by providing extensive high-quality instruction followed by layers of differentiation to meet the needs of different students, including high-achieving students.
Differentiation
“All students, regardless of their personal characteristics, backgrounds, or physical challenges, must have opportunities to study—and support to learn—mathematics. Equity does not mean that every student should receive identical instruction; instead, it demands that reasonable and appropriate accommodations be made as needed to promote access and attainment for all students” (NCTM, 2000, p.12).
Students in the classroom vary in important ways. Tomlinson (1997) puts it plainly, “Students are not all alike. They differ in readiness, interest, and learning profile” (p.1). Teachers today face the challenge of meeting the needs of an increasingly diverse student population. While it is critical that all students need high expectations for learning as well as access to high-quality instruction, it is also necessary that all students receive supports and differentiation each needs, regardless of socioeconomic background, if successful outcomes are to be achieved (Gutiérrez, 2013; NCTM, 2014).
Effective instructional approaches can meet the learning needs of all students, regardless of their background. According to Fuson, Math Expressions program author, and Smith (2015), children from poverty can develop high levels of conceptual understanding—so long as they are taught using instructional approaches that support the learning of concepts. When kindergarten, first-grade, and second-grade students from varied backgrounds had extensive opportunities to learn decomposing numbers and make drawings to solve addition and subtraction problems, they demonstrated high levels of performance. According to the researchers, “It is time to stop doing studies whose goal is to show that U.S. children or children from poverty do not understand math concepts. Now is the time for a substantive national discussion of instructional approaches that support the learning of concepts” (p.42).
Murata and Fuson (2007) also describe a class learning path model that individualizes within whole-class activities by eliciting the whole range of student methods in Phase 1 of teaching a new topic and then moving in Phase 2 to ensure that mathematically powerful but accessible methods are introduced, discussed, and compared. This model enables all students to participate in the class discussion and understand at least one method and move on to a better method with support of the teacher and students. This approach reduces the need for differentiating in special groups.
Talking about math has been found to benefit students at different levels of learning and in different contexts. In their study, Hufferd-Ackles, et al. (2004) found a Math-Talk community to be beneficial with students who were English learners in an urban setting. Similarly, working in a transitional language classroom led researchers Bray, Dixon, and Martinez (2006) to concluded that as students “communicate verbally and in writing about their mathematical ideas, they not only reflect on and clarify those ideas but also begin to become a community of learners” (p.138).
Intervention
Research has contributed to the development of response to intervention (RtI) models. These models frame differentiation as a prevention system with multiple layers—a structured way to prevent struggling students from falling behind—and so it focuses on early, and ongoing, identification of needs and tiers of responses. RtI integrates instruction, intervention, and assessment with the goal of increased student achievement (Mellard & Johnson, 2008).
Most commonly, RtI is implemented as a three-tier model where Tier 1 represents general instruction and constitutes primary prevention. Students at this level respond well to the general curriculum and learn reasonably well without additional support. Tier 2 represents a level of intervention for students who are at risk. Students at Tier 2 receive some supplementary support in the form of instruction or assessment. Tier 3 typically represents students who need more extensive and specialized intervention or special education services (Smith & Johnson, 2011).
A number of studies attest to the effectiveness of this kind of intervention approach. Ketterlin-Geller, Chard, and Fien (2008) saw improvement in mathematics performance on various achievement measures when underperforming students were given structured intervention support. Fuchs, Fuchs, and Hollenbeck (2007) looked at RtI in mathematics with students in Grade 1 (a comprehensive program) and Grade 3 (a focus on word problems). They found that the data supported RtI at both grade levels and showed “how two tiers of intervention, designed strategically to work in supplementary and coordinated fashion, may operate synergistically to decrease math problem-solving difficulties for children who are otherwise at risk for poor outcomes” (p.19).
A publication from the What Works Clearinghouse of the U.S. Department of Education (Gersten et al., 2009) presents an overview of research and best practice in RtI for the elementary and middle grades. At Tier 1, they recommend screening to identify those at risk. At Tiers 2 and 3, they recommend that:
- Grades K through 5 focus on whole numbers; Grades 4 through 8 on rational numbers.
- Intervention instruction is explicit and systematic.
- Intervention in mathematics should include:
- Models of problem solving – Word problems
- Graphic organizers
- Visual representations
- Practice for fluency
- Communication about math
- Students’ progress should be monitored, and include practice, feedback, and review.
- Interventions should be designed to motivate students (Gersten et al.2009).
Many years of research in classrooms provide the foundation for the Math Expressions program. This research produced learning paths for many topic areas that enables all children to learn. Knowledge of typical errors enables teachers to uncover and correct these quickly. The use of the class learning path model with the teaching phases and Math-Talk Learning Community enables the whole learning path to be active within the whole-class discussions and thus to differentiate within these whole-class discussions. The Mastery Learning Loop specifies that teachers keep teaching the lessons in each Big Idea (a part of a unit) and then have an intervention day. Another intervention day can occur if needed before the unit test. This enables many strugglers to catch up and stay on level. Students who are significantly behind or have special learning difficulties may require further special intervention. High-achieving and on-level students receive differentiated learning activities on the intervention day, so everyone gets some differentiation that follows initial high-quality instruction using the approaches summarized above.
Differentiation and Intervention in Math Expressions
In its approach to differentiation, Math Expressions has all of the characteristics described in the research findings above. Screening for Tier 1 is accomplished by the continual formative assessment occurring in the Math Talk and other parts of lessons, in quizzes, and in unit tests. The differentiation for all tiers and for on-level and advanced students occurs during the differentiation days as discussed in the Mastery Learning Loop. Tier 3 students receive further differentiation as needed.
With the program’s focus on visual learning, mathematical representations, and Math-Talk discussion, Math Expressions opens the world of mathematics to all learners, whatever their learning style. Math drawings can help all students see concepts and understand solutions. The program’s Math-Talk Learning Community approach is especially valuable for English learners and native speakers who need additional practice developing their verbal skills. These visual and verbal pathways allow students to use their strengths—visual-spatial or language—to shore up their weaker pathways and build a connected web of understanding.
On-Level, Challenge, and Intervention—Assessment and Intervention
The Children’s Math World (CMW) NSF-funded research upon which Math Expressions is based was conducted first in primarily urban, English- and Spanish-speaking classrooms and then later expanded into suburban schools with students of varied cultural backgrounds and diverse socioeconomic status. The Math Drawings and the use of MathBoards and Math Talk in the program are part of a teaching-learning approach designed to be particularly effective with students who have been historically underrepresented in math and science occupations and to result in equal opportunities to learn in the mathematics classroom.
The many informal classroom research projects at that time and two studies of kindergarten and Grade 1 children of poverty on their performance on the kinds of word problems (Fuson & Smith, 2015) found that students taught using Math Expressions, with an emphasis on math drawings and an opportunity to learn concepts, were able to reach high levels of performance with concepts. Other papers summarize instructional approaches that are central aspects in the Math Expressions classroom and were powerful for children of poverty and also for students already fluent in standard English and of diverse socioeconomic status and levels of math achievement. (For example, see Fuson et al., 2009; Fuson & Lo Cicero, 2000; Fuson, Lo Cicero, Hudson, & Smith, 1997; Lo Cicero, Fuson, & Allexaht-Snider, 1999.)
The model of balanced teaching using three phases was described earlier. This model ensures that there is a great deal of differentiation in the whole-classroom lessons for Math Expressions particularly because the teaching approaches in Math Expressions were developed and tested in a wide range of classrooms. To support the further differentiation described in the Mastery Learning Loop, a wide range of supports are available from which teachers can choose for the specified intervention days. For example, every lesson in Math Expressions includes intervention, on-level, and challenge differentiation to support students in their continued learning.
Support for English learners is included in every lesson. Other Math Expression features that support students learning English are:
- Expresiones en Matemáticas supports English learners with Spanish-language materials.
- The Bilingual eGlossary includes audio, graphics, and animation in both English and Spanish.
Math Expressions supports a response to intervention (RtI) instructional model. Support for all three tiers of intervention are located in the online Math Activity Center. To address student needs, Tiers 1 and 2 support uses interactive videos and Tier 3 includes a diagnostic assessment and a teacher-directed activity. A User Guide located with these online resources provides directions for using the Quick Quizzes to identify students who may need each type of intervention support.
Personal Math Trainer provides a digital path to intervention, with flexible options for addressing Tiers 1, 2, and 3, along with an assessment, management, and reporting system to track student progress.
Math Expressions is based on the results of the Children’s Math Worlds (CMW) research project, funded by the National Science Foundation (NSF), and is the only U.S. curriculum developed using the methods of learning science design research. Math Expressions author Dr. Karen Fuson’s work leading the CMW research project was foundational in identifying the key components for successful mathematics learning, the focus and sequence of content, and the effective instructional practices built into Math Expressions.
As part of the CMW research project, work was done in classrooms and in interviews for four to five years on major topics at each grade level, with continual revision of the teaching and learning materials. The goal was to identify supported learning paths through major math domains that could be coherently woven across grades. The research tasks included:
- Identifying typical student errors and how to overcome them
- Developing accessible and mathematically desirable algorithms that relate to common algorithms but that all students can understand and explain
- Choosing math drawings that facilitate understanding of the domain situations or quantities
Listed below are papers reporting research on which Math Expressions is based. The following papers describe (1) research on teaching and learning that provides part of the research base from which the Children’s Math Worlds Research Project (CMW) was developed and (2) research reports that document the individual design studies and their success with students. More research papers exist in draft and research summary form based on the intensive ten-year period of progressive refinement of the curriculum using extensive observations and feedback from teachers, and more papers will be written to summarize research results in other areas.
These articles describe central aspects of Math Expressions classrooms in action to create communication, confidence, and competence.
Fuson, K.C., Atler, T., Roedel, S., & Zaccariello, J. (2009). Building a nurturing, visual, Math-Talk teaching-learning community to support learning by English language learners and students from backgrounds of poverty. New England Mathematics Journal, XLI(May), 6–16.
Fuson, K.C., De La Cruz, Y., Smith, S., Lo Cicero, A., Hudson, K., Ron, P., & Steeby, R. (2000). Blending the best of the 20th century to achieve a mathematics equity pedagogy in the 21st century. In M.J. Burke & F.R. Curcio (Eds.), Learning mathematics for a new century (pp.197–212). Reston, VA: National Council of Teachers of Mathematics.
Hufferd-Ackles, K., Fuson, K.C., & Sherin, M.G. (2004). Describing levels and components of a Math-Talk Learning Community. Journal for Research in Mathematics Education, 35(2), 81–116.
Hufferd-Ackles, K., Fuson, K.C., & Sherin, M.G. (2015). Describing levels and components of a Math-Talk Learning Community. In E.A. Silver & P.A. Kenney (Eds.), More lessons learned from research: Volume 1: Useful and usable research related to core mathematical practices (pp.125–134). Reston, VA: NCTM.
These articles describe the balanced learning path teaching approach used in Math Expressions classrooms.
Fuson, K.C. (2009). Avoiding misinterpretations of Piaget and Vygotsky: Mathematical teaching without learning, learning without teaching, or helpful learning-path teaching? Cognitive Development, 24(4), 343–361.
Fuson, K.C., & Murata, A. (2007). Integrating NRC principles and the NCTM Process Standards to form a Class Learning Path Model that individualizes within whole-class activities. National Council of Supervisors of Mathematics. Journal of Mathematics Education Leadership, 10(1), 72–91.
Fuson, K.C., Murata, A., & Abrahamson, D. (2014). Using learning path research to balance mathematics education: Teaching/learning for understanding and fluency. In R. Cohen Kadosh & A. Dowker (Eds.), Oxford handbook of numerical cognition. Oxford Handbooks Online (pp.1036–1054). Oxford, England: Oxford University Press.
Murata, A., & Fuson, K.C. (2006).Teaching as assisting individual constructive paths within an interdependent class learning zone: Japanese first graders learning to add using ten. Journal for Research in Mathematics Education, 37(5), 421–456.
These articles summarize effective ways to teach computation and word problems.
Fuson, K.C. (1992). Research on whole number addition and subtraction. In D. Grouws (Ed.), Handbook of research on mathematics teaching and learning (pp.243–275). New York: Macmillan.
Fuson, K.C. (2003). Developing mathematical power in whole number operations. In J. Kilpatrick, W.G. Martin, & D. Schifter (Eds.), A research companion to Principles and Standards for School Mathematics (pp.68–94). Reston, VA: National Council of Teachers of Mathematics.
These articles describe central aspects of developing a Math Expressions classroom in urban Latino classrooms, where CMW started. (Later research tested the curricular approaches in a wide range of schools, including advantaged schools with many high-achieving students, but the initial research was conducted in urban schools with diverse populations, including many underrepresented minorities and English learners.)
Fuson, K.C., & Lo Cicero, A. (2000). El Mercado in Latino primary math classrooms. In M.L. Fernandez (Ed.), Proceedings of the Twenty-Second Annual Meeting of the North American Chapter of the International Group for the Psychology of Mathematics Education (Vol.2, p.453). Columbus, OH: ERIC Clearinghouse for Science, Mathematics, and Environmental Education.
Fuson, K.C., Lo Cicero, A., Hudson, K., & Smith, S.T. (1997). Snapshots across two years in the life of an Urban Latino Classroom. In J. Hiebert, T. Carpenter, E. Fennema, K.C. Fuson, D. Wearne, H. Murray, A. Olivier, & P. Human. Making sense: teaching and learning mathematics with understanding (pp.129–159). Portsmouth, NH: Heinemann.
Lo Cicero, A., Fuson., K.C., & Allexaht-Snider, M. (1999). Making a difference in Latino children’s math learning: Listening to children, mathematizing their stories, and supporting parents to help children. In L. Ortiz-Franco, N.G. Hernandez, & Y. De La Cruz (Eds.), Changing the faces of mathematics: Perspectives on Latinos (pp.59–70). Reston, VA: National Council of Teachers of Mathematics.
These articles describe the ways that Math Expressions approaches in kindergarten support ambitious, international levels of conceptions of teen numbers as tens and ones, as well as embedded numbers that can support advanced addition and subtraction methods.
Fuson, K.C., Grandau, L., & Sugiyama, P.A. (2001). Achievable numerical understandings for all young children. Invited paper for the “Research into Practice” series. Teaching Children Mathematics, 7(9), 522–526.
Ho, C.S., & Fuson, K.C. (1998). Children’s knowledge of teens quantities as tens and ones: Comparisons of Chinese, British, and American kindergartners. Journal of Educational Psychology, 90(3), 536–544.
Other papers are being prepared for publication.
These articles describe the learning path in single-digit addition and subtraction moving to powerful and general methods.
Duncan, A., Lee, H., & Fuson, K.C. (2000). Pathways to early number concepts: Use of 5- and 10-structured representations in Japan, Taiwan, and the United States. In M.L. Fernandez (Ed.), Proceedings of the Twenty-Second Annual Meeting of the North American Chapter of the International Group for the Psychology of Mathematics Education (Vol.2, p.452). Columbus, OH: ERIC Clearinghouse for Science, Mathematics, and Environmental Education.
Fuson, K.C. (1986). Teaching children to subtract by counting up. Journal for Research in Mathematics Education, 17(3), 172–189. (This paper was chosen as the best research article of 1986 by the Research Advisory Council of the National Council of Teachers of Mathematics.)
Fuson, K.C. (1987). Adding by counting on with one-handed finger patterns. The Arithmetic Teacher, 35(1), 38–41. (Invited paper; first article in the new “Research into Practice” series.)
Fuson, K.C. (1988). Subtracting by counting up with one-handed finger patterns. The Arithmetic Teacher, 35(5), 29–31. (Invited paper for the “Research into Practice” series.)
Fuson, K. C., & Kwon, Y. (1992). Korean children’s single-digit addition and subtraction: Numbers structured by ten. Journal for Research in Mathematics Education, 23(2), 148–165.
Fuson, K.C., Perry, T., & Kwon, Y. (1994). Latino, Anglo, and Korean children’s finger addition methods. In J.E.H. van Luit (Ed.), Research on learning and instruction of mathematics in kindergarten and primary school (pp.220–228). Doetinchem/Rapallo, The Netherlands: Graviant.
Fuson, K. C., & Secada, W. G. (1986). Teaching children to add by counting on with finger patterns. Cognition and Instruction, 3(3), 229–260.
Murata, A., & Fuson, K.C. (2001). Learning paths to 5- and 10-structured understanding of quantity: Addition and subtraction solution strategies of Japanese children. In R. Speiser, C.S. Maher, & C. Walter (Eds.) Proceedings of the Twenty-Third Annual Meeting of the North American Chapter of the International Group for the Psychology of Mathematics Education (Vol.2, pp.639–646). Columbus, OH: ERIC Clearinghouse for Science, Mathematics, and Environmental Education.
Murata, A., & Fuson, K. C. (2006). Teaching as assisting individual constructive paths within an interdependent class learning zone: Japanese first graders learning to add using ten. Journal for Research in Mathematics Education, 37(5), 421–456.
These articles describe the learning path in multi-digit addition and subtraction moving to powerful and general methods.
Fuson, K. C. (1990). Conceptual structures for multiunit numbers: Implications for learning and teaching multidigit addition, subtraction, and place value. Cognition and Instruction, 7(4), 343–403.
Fuson, K. C. (1990). Issues in place-value and multidigit addition and subtraction learning and teaching. Journal for Research in Mathematics Education, 21(4), 273–280.
Fuson, K. C., & Beckmann, S. (Fall/Winter, 2012–2013). Standard algorithms in the Common Core State Standards. Journal of Mathematics Education Leadership, 14(2), 14–30.
Fuson, K. C., & Burghardt, B. H. (2003). Multi-digit addition and subtraction methods invented in small groups and teacher support of problem solving and reflection. In A. J. Baroody & A. Dowker (Eds.), The development of arithmetic concepts and skills: Constructing adaptive expertise (pp. 267–304). Mahwah, NJ: Lawrence Erlbaum Associates.
Fuson, K. C., & Kwon, Y. (1991). Chinese-based regular and European irregular systems of number words: The disadvantages for English-speaking children. In K. Durkin & B. Shire (Eds.), Language and mathematical education (pp. 211–226). Milton Keynes, UK: Open University Press.
Fuson, K. C., & Kwon, Y. (1992). Korean children’s understanding of multidigit addition and subtraction. Child Development, 63(2), 491–506.
Fuson, K. C., & Li, Y. (2009). Cross-cultural issues in linguistic, visual-quantitative, and written-numeric supports for mathematical thinking. ZDM – The International Journal on Mathematics Education, 41(6), 793–808.
Fuson, K. C., & Li, Y. (2014). Learning paths and learning supports for conceptual addition and subtraction in the U.S. Common Core State Standards and in the Chinese Standards. In Y. Li & G. Lappan (Eds.), Mathematics curriculum in school education (pp. 541–558). Dordrecht, Germany: Springer.
Fuson, K. C., & Smith, S. T. (1995). Complexities in learning two-digit subtraction: A case study of tutored learning. Mathematical Cognition, 1(2), 165–213.
Fuson, K. C., & Smith, S. T. (1997). Supporting multiple 2-digit conceptual structures and calculation methods in the classroom: Issues of conceptual supports, instructional design, and language. In M. Beishuizen, K.P.E. Gravemeijer, & E.C.D.M. van Lieshout (Eds.), The role of contexts and models in the development of mathematical strategies and procedures (pp. 163–198). Utrecht, The Netherlands: CD-B Press/The Freudenthal Institute.
Fuson, K. C., Smith, S. T., & Lo Cicero, A. (1997). Supporting Latino first graders’ ten-structured thinking in urban classrooms. Journal for Research in Mathematics Education, 28(6), 738–766.
Fuson, K. C., Wearne, D., Hiebert, J., Human, H., Murray, A., Olivier, A., Carpenter, T., & Fennema, E. (1997). Children’s conceptual structures for multidigit numbers and methods of multidigit addition and subtraction. Journal for Research in Mathematics Education, 28(2), 130–162.
These articles describe the learning path in teaching and learning the full range of word problems.
Fuson, K.C. (1988). First and second graders’ ability to use schematic drawings in solving twelve kinds of addition and subtraction word problems. In M.J. Behr, C.B. Lacampagne, & M.M. Wheeler (Eds.), Proceedings of the Tenth Annual Meeting of the North American Chapter of the International Group for the Psychology of Mathematics Education (pp.364–370). DeKalb, IL: Northern Illinois University.
Fuson, K.C., Carroll, W.M., & Landis, J. (1996). Levels in conceptualizing and solving addition/subtraction compare word problems. Cognition and Instruction, 14(3), 345–371.
Fuson, K.C., & Willis, G.B. (1989). Second graders’ use of schematic drawings in solving addition and subtraction word problems. Journal of Educational Psychology, 81(4), 514–520.
Lo Cicero, A., De La Cruz, Y., & Fuson, K.C. (1999). Teaching and learning creatively: Using children’s narratives. Teaching Children Mathematics, 5(9), 544–547.
Stigler, J., Fuson, K.C., Ham, M., & Kim, M.S. (1986). An analysis of addition and subtraction word problems in Soviet and American elementary textbooks. Cognition and Instruction, 3(3), 153–171.
These articles describe the learning path in single-digit and multi-digit multiplication and division leading to powerful and general methods.
Fuson, K.C., & Beckmann, S. (Fall/Winter, 2012–2013). Standard algorithms in the Common Core State Standards. National Council of Supervisors of Mathematics Journal of Mathematics Education Leadership, 14(2), 14–30.
Izsák, A. (2001). Learning multi-digit multiplication by modeling rectangles. In R. Speiser, C. Maher, & C. Walter (Eds.). Proceedings of the Twenty-Third Annual Meeting of the North American Chapter of the International Group for the Psychology of Mathematics Education (Vol.1, pp.187–194). Columbus, OH: ERIC Clearinghouse for Science, Mathematics, and Environmental Education.
Izsák A. (2004).Teaching and learning two-digit multiplication: Coordinating analyses of classroom practices and individual student learning. Mathematical Thinking and Learning, 6(1), 37–79.
Izsák, A. (2005). “You have to count the squares”: Applying knowledge in pieces to learning rectangular area. The Journal of the Learning Sciences, 14(3), 361–403.
Izsák, A., & Fuson, K.C.(2000).Students’ understanding and use of multiple representations while learning two-digit multiplication. In M.L. Fernandez (Ed.), Proceedings of the Twenty-Second Annual Meeting of the North American Chapter of the International Group for the Psychology of Mathematics Education (Vol.2, pp.714–721). Columbus, OH: ERIC Clearinghouse for Science, Mathematics, and Environmental Education.
Izsák, A., & Sherin, M. (2003). Exploring the use of new representations as a resource for teacher learning. School Science and Mathematics, 103(1), 18–27.
Sherin, B., & Fuson, K.C. (2005).Multiplication strategies and the appropriation of computational resources. Journal for Research in Mathematics Education, 36(4), 347–395.
Sherin, M., & Izsák, A. (2001). Representations as a resource for teacher learning. In R. Speiser, C. Maher, & C.Walter (Eds.), Proceedings of the Twenty-Third Annual Meeting of the North American Chapter of the International Group for the Psychology of Mathematics Education (Vol.2, pp.961–962). Columbus, OH: ERIC Clearinghouse for Science, Mathematics, and Environmental Education.
Abrahamson, D. (2002). When “the same” is the same as different differences: Aliya reconciles her perceptual judgment of proportional equivalence with her additive computation skills. In D. Mewborn, P. Sztajn, E. White, H. Wiegel, R. Bryant, & K. Nooney (Eds.), Proceedings of the Twenty Fourth Annual Meeting of the North American Chapter of the International Group for the Psychology of Mathematics Education (Vol.4, pp.1658–1661). Columbus, OH: Eric Clearinghouse for Science, Mathematics, and Environmental Education.
Abrahamson, D. (2003). Text talk, body talk, table talk: A design of ratio and proportion as classroom parallel events. In N.A. Pateman, B.J. Dougherty, & J.T. Zilliox (Eds.), Twenty Seventh Annual Meeting of the International Group for the Psychology of Mathematics Education (Vol.2, pp.1–8). Columbus, OH: Eric Clearinghouse for Science, Mathematics, and Environmental Education.
Abrahamson, D., & Cigan, C. (2003). A design for ratio and proportion. Mathematics teaching in the middle school, 8(9), 493–501.
Abrahamson, D., Lee, R.G., Negrete, A.G., & Gutiérrez, J.F. (2014). Coordinating visualizations of polysemous action: values added for grounding proportion. In F. Rivera, H. Steinbring, & A. Arcavi (Eds.), Visualization as an epistemological learning tool [Special issue]. ZDM–The international Journal on Mathematics Education, 46(1), 79–93.
Fuson, K.C. (2008, April). Differentiating fractions and ratios and teaching both coherently and with understanding. Paper given at the Annual Conference of the National Council of Supervisors of Mathematics, Salt Lake City, UT.
Fuson, K.C. (2010, April). Modeling and relating fractions and ratios within the multiplication table. Paper given at the Annual Conference of the National Council of Teachers of Mathematics, San Diego, CA.
Fuson, K.C. (2012, October). Ratio, proportion, and fractions. Paper presented as a featured talk in the Department of Mathematics, Rome University, Rome, Italy.
Fuson, K.C., & Abrahamson, D. (2005). Understanding ratio and proportion as an example of the apprehending zone and conceptual-phase problem-solving models. In J. Campbell (Ed.), Handbook of mathematical cognition (pp.213–234). New York: Psychology Press.
Fuson, K.C., & Beckmann, S. (2012, April). Multiplication to ratio, proportion, and fractions within the Common Core. Paper presented at the annual meeting of the National Council of Teachers of Mathematics, Philadelphia, PA.
Fuson, K.C., & Kalchman, M. (2002). A length model of fractions puts multiplication of fractions in the learning zone of fifth graders. In D.L. Haury (Ed.), Proceedings of the Twenty-Fourth Annual Meeting of the North American Chapter of the International Group for the Psychology of Mathematics Education (pp.1641–1649). Columbus, OH: ERIC Clearinghouse for Science, Mathematics, and Environmental Education.
Abrahamson, D. (2002). When “the same” is the same as different differences: Aliya reconciles her perceptual judgment of proportional equivalence with her additive computation skills. In D. Mewborn, P. Sztajn, E. White, H. Wiegel, R. Bryant, & K. Nooney (Eds.), Proceedings of the Twenty Fourth Annual Meeting of the North American Chapter of the International Group for the Psychology of Mathematics Education (Vol.4, pp.1658–1661). Columbus, OH: Eric Clearinghouse for Science, Mathematics, and Environmental Education.
Abrahamson, D. (2003). Text talk, body talk, table talk: A design of ratio and proportion as classroom parallel events. In N. A. Pateman, B. J. Dougherty, & J. T. Zilliox (Eds.), Twenty Seventh Annual Meeting of the International Group for the Psychology of Mathematics Education (Vol. 2, pp. 1–8). Columbus, OH: Eric Clearinghouse for Science, Mathematics, and Environmental Education.
Abrahamson, D., & Cigan, C. (2003). A design for ratio and proportion. Mathematics Teaching in the Middle School, 8(9), 493–501.
Abrahamson, D., Lee, R. G., Negrete, A. G., & Gutiérrez, J. F. (2014). Coordinating visualizations of polysemous action: values added for grounding proportion. In F. Rivera, H. Steinbring, & A. Arcavi (Eds.), Visualization as an epistemological learning tool [Special issue]. ZDM–The international Journal on Mathematics Education, 46(1), 79–93.
Agodini, R., Harris, B., Thomas, M., Murphy, R., & Gallagher, L. (2010). Achievement effects of four early elementary school math curricula: Findings for first and second graders (NCEE 2011–4001). Washington, DC: U.S. Department of Education.
Alberti, S. (2013). Making the shifts. Educational Leadership, December 2012/January 2013, 24–27.
American Educational Research Association, American Psychological Association, and National Council on Measurement in Education. (1999). Standards for Educational and Psychological Testing. 5th ed. Washington, DC: American Educational Research Association.
Arcavi, A. (2003). The role of visual representations in the learning of mathematics. Educational Studies in Mathematics, 52(3), 215–241.
Aspinwall L., & Aspinwall J. (2003). Investigating mathematical thinking using open writing prompts. Mathematics Teaching in the Middle School, 8(7), 350–353.
Baker, S., Gersten, R., & Lee, D. (2002). A synthesis of empirical research on teaching mathematics to low-achieving students. The Elementary School Journal, 103(1), 67.
Baker, S., Schirner, K., & Ho man, J. (2006). Multiage mathematics: Scaffolding young children’s mathematical learning. Teaching Children Mathematics, 13(1), 19–21.
Baldi, S., Jin, Y., Skemer, M., Green, P. J., & Herget, D. (2007). Highlights from PISA 2006: Performance of U.S. 15-year-old students in science and mathematics literacy in an international context. National Center for Education Statistics. U.S. Department of Education: NCES 2008-016. Washington, DC: American Institutes for Research.
Ball, D. L. (1992a). Constructing new forms of teaching: Subject matter knowledge in in-service teacher education. Journal of Teacher Education, 43(5), 347–356.
Ball, D. L. (1992b). Magical hopes: Manipulatives and the reform of math education. American Educator, 16(2), 14.
Baroody, A. J. (2006). Why children have difficulties mastering the basic number combinations and how to help them. Teaching Children Mathematics, 13(1), 22–32.
Beane, J. A (1997). Curriculum integration: Designing the core of democratic education. Alexandria, VA: Association for Supervision and Curriculum Development.
Black, P., & Wiliam, D. (1998). Assessment and classroom learning. Assessment in Education: Principles, Policy, and Practice, 5(1), 7–73.
Blackwell, L. S., Trzesniewski, K. H., & Dweck, C. S. (2007). Implicit theories of intelligence predict achievement across an adolescent transition: A longitudinal study and an intervention. Child Development, 78(1), 246–263.
Blatto-Vallee, G., Kelly, R., Gaustad, M., Porter, J., & Fonzi, J. (2007). Visual spatial representation in mathematical problem solving by deaf and hearing students. Journal of Deaf Students and Deaf Education, 12(4), 432–448.
Boaler, J. (1998). Open and closed mathematics: Student experiences and understandings. Journal for Research in Mathematics Education, 29, 41–62.
Boaler, J. (2011). Changing students’ lives through the de-tracking of urban mathematics classrooms. Journal of Urban Mathematics Education, 4(1), 7–14.
Boaler, J. (2016). Mathematical mindsets. Hoboken, NJ: Wiley Press.
Boaler, J., & Staples, M. (2008). Creating mathematical futures through an equitable teaching approach: The case of Railside School. Teachers College Record, 110(3), 608–645.
Bobis, J., & Way, J. (2018). Building connections between children’s representations and their conceptual development in mathematics. In V. Kinnear, M. Lai, & T. Muir (Eds), Forging connections in early mathematics teaching and learning. Early Mathematics Learning and Development. Singapore: Springer.
Booth, J. L., Lange, K. E., Koedinger, K. R., & Newton, K. J. (2013). Using example problems to improve student learning in algebra: Differentiating between correct and incorrect examples. Learning and Instruction, 25(2), 24–34.
Boston, M. D., & Wilhelm, A. G. (2015). Middle school mathematics instruction in instructionally focused urban districts. Urban Education, 1–33.
Bransford, J. D., Brown, A. L., & Cocking, R. R. (Eds.). (1999). How people learn: Brain, mind, experience, and school. National Research Council. Washington, DC: National Academies Press.
Bray, W. S., Dixon, J. K., & Martinez, M. (2006). Fostering communication about measuring area in a transitional language class. Teaching Children Mathematics, 13(3), 132–138.
Bryant, C. (2015). Mathematical habits of mind. Edutopia. Retrieved from: https://www.edutopia.org/blog/...
Caine, R. N., & Caine, G. (1994). Making connections: Teaching and the human brain. Alexandria, Virginia: Association for Supervision and Curriculum Development.
Carnegie Mellon. (2015). Formative versus summative assessment. (Online). Retrieved from: www.cmu.edu/teaching/assessment/basics/formative-summative.html
Carpenter, T. P., Fennema, E., Franke, M. L., Levi, L., & Empson, S. B. (2015). Children’s mathematics. Cognitively guided instruction. Portsmouth, NH: Heinemann.
Carpenter, T. P., Franke, M. L., & Levi, L. (2003). Thinking mathematically: Integrating arithmetic and algebra in elementary schools. Portsmouth, NH: Heinemann.
CDW. (2011). 2011 CDW-G 21st-century classroom report. Retrieved from: http://webobjects.cdw.com/webo...
Cepeda, N., Coburn, N., Rohrer, D., Wixted, J., Mozer, M., & Pashler, H. (2009). Optimizing distributed practice: Theoretical analysis and practical implications. Experimental Psychology, 56(4), 236–246.
Cepeda, N., Pashler, H., Vul, E., Wixted, J., & Rohrer, D. (2006). Distributed practice in verbal recall tasks: A review and quantitative synthesis. Psychological Bulletin, 132(3), 354–380.
Chamberlin, M. T., & Powers, R. A. (2010). The promise of differentiated instruction for enhancing the mathematical understandings of college students. Teaching Mathematics and its Applications: An International Journal of the Institute of Mathematics and its Applications, 29(3), 113–139.
Chapin, S. H., O’Connor, C., & Canavan Anderson, N. (2003). Classroom discussions: Using Math Talk to help students learn, Grades 1-6. Sausalito, CA: Math Solutions Publication.
Charles, R. I. (2005). Big ideas and understandings as the foundation for elementary and middle school mathematics. Journal of Mathematics Education Leadership, 7(3), 9–24.
Chetty, R., Friedman, J. N., & Rockoff, J. E. (2012) Great teaching: Measuring its effects on students’ future earnings. Education Next, 12(3), 58–64.
Christenson, S. L., Ysseldyke, J. E., & Thurlow, M. L. (1989). Critical instructional factors for students with mild handicaps: An integrative review. Remedial and Special Education, 10(5), 21–31.
Clarke, B., & Shinn, M. R. (2004). A preliminary investigation into the identification and development of early mathematics curriculum-based measurement. School Psychology Review, 33(2), 234−248.
Clarke, S., Timperley, H., & Hattie, J. (2004). Unlocking formative assessment: practical strategies for enhancing students’ learning in the primary and intermediate classroom. Auckland, New Zealand: Hodder Moa Beckett.
Clements, D. H. (2003). Teaching and learning geometry. In J. Kilpatrick, W. G. Martin, & D. Schifter (Eds.), A research companion to Principles and Standards for School Mathematics (pp. 151–178). Reston, VA: National Council of Teachers of Mathematics.
Clements, D. H., & McMillen, S. (1996). Rethinking “concrete” manipulatives. Teaching Children Mathematics, 2(5), 270–227.
Clements, D. H., & Sarama, J. (2004). Learning trajectories in mathematics education. Mathematical Thinking and Learning, 6(2), 81–89.
Clements, D. H., & Sarama, J. (2007a). Early childhood mathematics learning. In F. K. Lester, Jr. (Ed.), Second handbook of research on mathematics teaching and learning (pp. 461−555). New York: Information Age.
Clements, D. H., & Sarama, J. (2007b). Effects of a preschool mathematics curriculum: Summative research on the “Building Blocks” project. Journal for Research in Mathematics Education, 38(2), 136–163.
College Board. (2011). Forty-three percent of 2011 college-bound seniors met SAT college and career readiness benchmark [Press release]. Retrieved from http://press.collegeboard.org/releases/2011/43-percent-2011-college-bound-seniors-met-sat- college-and-careerreadinessbenchmark.
Cotton, K. (1995). Effective schooling practices: A research synthesis 1995 update. Portland, OR: Northwest Regional Educational Laboratory. Retrieved from: http:// www.kean.edu/~lelovitz/docs/ED...
Cross, C. T., Woods, T. A., & Schweingruber, H. (Eds.). (2009). Mathematics learning in early childhood: Paths toward excellence and equity. Center for Education, Division of Behavioral and Social Science and Education. Washington, DC: National Academy Press.
Cuoco, A., Goldenberg, E. P., & Mark, J. (1996). Habits of mind: An organizing principle for mathematics curricula. Journal of Mathematical Behavior, 15(4), 375–402.
Czerniak, C. M., Weber, W. B., Jr., Sandmann, A., & Ahem, J. (1999). A literature review of science and mathematics integration. School Science & Mathematics, 99(8), 421–430.
Darling-Hammond, L. (2010). Performance counts: Assessment systems that support high-quality learning. Washington, DC: Council of Chief State School Officers.
David, J., & Greene, D. (2007). Improving mathematics instruction in Los Angeles high schools: An evaluation of the prisma pilot program. Palo Alto, CA.: Bay Area Research Group.
Demirsky Allan, S., & Goddard, Y. L. (2010). Differentiated instruction and RtI: A natural fit. Interventions that Work, 68(2), online.
Dickinson, D., & Smith, M. W. (1993). Long-term effects of preschool teachers’ book readings on low-income children’s vocabulary and story comprehension. Reading Research Quarterly, 29(2), 104–122.
Dixon, J. (2018). Just-in-time vs. just-in-case scaffolding: How to foster productive perseverance. Retrieved from: /blog/jus...
Dweck, C. (2006). Mindset: The new psychology of success. New York: Random House.
Dweck, C. (2008). Mindsets and math/science achievement. New York: Carnegie Corporation of New York Institute for Advanced Study.
Fadel, C., Honey, M., & Pasnik, S. (2007). Assessment in the age of innovation. Education Week. Bethesda, MD: Editorial Projects in Education.
Fosnot, C.T., & Dolk, M. (2001). Young mathematicians at work: Constructing multiplication and division. Portsmouth, NH: Heinemann.
Fosnot, C.T., & Jacob, W. (2010). Young mathematicians at work: Constructing algebra. Portsmouth, NH: Heinemann.
Fox, J. (2004). Test decisions over time: Tracking validity. Language Testing, 21, 437–465.
Franke, M.L., Kazemi, E., & Battey, D.S. (2007). Mathematics teaching and classroom practices. In F.K. Lester Jr.(Ed.), The second handbook of research on mathematics teaching and learning (pp.225–256). Charlotte, NC: Information Age.
Freeman, B., & Crawford, L. (2008). Creating a middle school mathematics curriculum for English language learners. Remedial and Special Education, 29(1), 9–19.
Fuchs, D., & Fuchs, L.S. (2006). Introduction to Response to Intervention: What, why, and how valid is it? Reading Research Quarterly, 41(1), 93–99.
Fuchs, L.S. (2004). The past, present, and future of curriculum-based measurement research. School Psychology Review, 33, 188–192.
Fuchs, L.S., Fuchs, D., & Hollenbeck, K.N. (2007). Extending responsiveness to intervention to mathematics at first and third grades. Learning Disabilities Research & Practice, 22(1), 13–24.
Fuson, K.C. (1986). Roles of representation and verbalization in the teaching of multidigit addition and subtraction.European Journal of Psychology in Education, 4, 35–56.
Fuson, K.C. (2009). Avoiding misinterpretations of Piaget and Vygotsky: Mathematical teaching without learning, learning without teaching, or helpful learning-path teaching? Cognitive Development, 24(4), 343–361.
Fuson, K.C. (2008, April). Differentiating fractions and ratios and teaching both coherently and with understanding. Paper given at the Annual Conference of the National Council of Supervisors of Mathematics, Salt Lake City, UT.
Fuson, K.C. (2010, April). Modeling and relating fractions and ratios within the multiplication table. Paper given at the Annual Conference of the National Council of Teachers of Mathematics, San Diego, CA.
Fuson, K.C. (2012, October). Ratio, proportion, and fractions. Paper presented as a featured talk in the Department of Mathematics, Rome University, Rome, Italy.
Fuson, K.C., & Abrahamson, D. (2005). Understanding ratio and proportion as an example of the apprehending zone and conceptual-phase problem-solving models. In J. Campbell (Ed.), Handbook of mathematical cognition (pp.213–234). New York: Psychology Press.
Fuson, K.C., & Beckmann, S. (2012, April). Multiplication to ratio, proportion, and fractions within the Common Core. Paper presented at the annual meeting of the National Council of Teachers of Mathematics, Philadelphia, PA.
Fuson, K.C., & Beckmann, S. (Fall/Winter 2012–2013). Standard algorithms in the Common Core State Standards. National Council of Supervisors of Mathematics Journal of Mathematics Education Leadership, 14(2), 4–30.
Fuson, K.C., & Kalchman, M. (2002). A length model of fractions puts multiplication of fractions in the learning zone of fifth graders. In D.L. Haury (Ed.), Proceedings of the Twenty-Fourth Annual Meeting of the North American Chapter of the International Group for the Psychology of Mathematics Education (pp.1641–1649). Columbus, OH: ERIC Clearinghouse for Science, Mathematics, and Environmental Education.
Fuson, K.C., & Murata, A. (2007). Integrating NRC principles and NCTM process standards to form a class learning path model that individualizes within whole-class activities. The National Council of Supervisors of Mathematics Journal of Mathematics Education Leadership, 10(1), 72–91.
Fuson, K.C., & Smith, S.T. (2015). Word problem solving by children from backgrounds of poverty: Are the Common Core OA State Standards in the learning zone of low SES children? Manuscript.
Fuson, K.C., & Willis, G.B. (1989). Second graders’ use of schematic drawings in solving addition and subtraction word problems. Journal of Educational Psychology, 81(4), 514–520.
Fuson, K.C., Atler, T., Roedel, S., & Zaccariello, J. (2009). Building a nurturing, visual, Math-Talk teaching-learning community to support learning by English language learners and students from backgrounds of poverty. New England Mathematics Journal, XLI(May), 6–16.
Fuson, K., Clements, D.& Sarama, J. (2015). Making early math education work for all children. Kappan Magazine, 97(3), 63–68.
Fuson, K.C., De La Cruz, Y., Smith, S., Lo Cicero, A., Hudson, K., Ron, P., & Steeby, R. (2000). Blending the best of the 20th century to achieve a mathematics equity pedagogy in the 21st century. In M.J. Burke and F.R. Curcio (Eds.), Learning mathematics for a new century (pp.197–212). Reston, VA: NCTM.
Fuson, K.C., Kalchman, M., & Bransford, J.D. (2005). Mathematical understanding: An introduction. In M.S. Donovan & J.D. Bransford (Eds.), How students learn: History, math, and science in the classroom (pp.217– 256). Washington, DC: National Academy Press.
Fuson, K.C., Lo Cicero, A., Hudson, K., & Smith, S.T. (1997). Snapshots across two years in the life of an Urban Latino Classroom. In J. Hiebert, T. Carpenter, E. Fennema, K.C. Fuson, D. Wearne, H. Murray, A. Olivier, & P. Human, Making sense: teaching and learning mathematics with understanding (pp.129–159). Portsmouth, NH: Heinemann.
Fuson, K.C., Smith, S.T., & Lo Cicero, A. (1997). Supporting Latino first graders’ ten-structured thinking in urban classrooms. Journal for Research in Mathematics Education, 28(6), 738–766.
Gaddy, A.K., Harmon, S.E., Barlow, A.T., Milligan, C.D., & Huang, R. (2014). Implementing the Common Core: Applying shifts to instruction. Mathematics Teacher, 108(2), 108–113.
Gersten, R., Beckmann, S., Clarke, B., Foegen, A., Marsh, L., Star, J.R., & Witzel, B. (2009). Assisting students struggling with mathematics: Response to Intervention (RtI) for elementary and middle schools. Institute of Education Sciences What Works Clearinghouse. Washington, DC: U.S. Department of Education. Retrieved from: http://ies.ed.gov/ncee/wwc/pdf...
Gersten, R., & Chard, D. (2001). Number sense: Rethinking arithmetic instruction for students with mathematical disabilities. LD OnLine. Retrieved from: http://www.ldonline.org/article/5838/
Gersten, R., & Clarke, B.S. (2007). Effective strategies for teaching students with difficulties in mathematics. Instruction Research Brief. Reston, VA: National Council of Teachers of Mathematics.
Ginsburg, A., Cooke, G., Leinwand, S., Noell, J., & Pollock, E. (2005). Reassessing U.S. international mathematics performance: New findings from the 2003 TIMSS and PISA. Prepared for U.S. Department of Education Policy and Program Studies Service (PPSS). Washington, DC: American Institutes for Research (AIR). Retrieved from: http://www.air.org/files/TIMSS...
Goldenberg, E., Mark, J., Kang, J., Fries, M., Carter, C., & Cordner, T. (2015). Making sense of algebra: Developing students’ mathematical habits of mind. Portsmouth, NH: Heinemann.
Goldhaber, D. (2002). The mystery of good teaching: Surveying the evidence on student achievement and teachers’ characteristics. Education Next, 2(1), 50–55.
Gonzales, P., Williams, T., Jocelyn, L., Roey, S., Katsberg, D., & Brenwald, S. (2008). Highlights from TIMSS 2007: Mathematics and science achievement of U.S. fourth- and eighth-grade students in an international context (NCES 2009-001 Revised). National Center for Education Statistics, Institute of Education Sciences. Washington, DC: U.S. Department of Education.
Good, J.M., & Whang, P.A. (1999). Making meaning in educational psychology with student response journals. Paper presented at the annual meeting of the American Educational Research Association, Montreal, Canada.
Griffiths, A., VanDerHeyden, A.M., Parson, L.B., & Burns, M.K. (2006). Practical applications of Response-to-Intervention research. Assessment for Effective Intervention, 32(1), 50–57.
Grupe, L.A., & Bray, N.W. (1999). What role do manipulatives play in kindergartners’ accuracy and strategy use when solving simple addition problems? Albuquerque, NM: Society for Research in Child Development.
Gutiérrez, R. (2013). The sociopolitical turn in mathematics education. Journal for Research in Mathematics Education 44, (1), 37–68.
Hall, T., Strangman, N., & Meyer, A. (2009). Differentiated instruction and implications for UDL implementation. Wakefield, MA: National Center on Accessing the General Curriculum.
Hatano, G., & Inagaki, K. (1991). Constrained person analogy in young children’s biological inference. Cognitive Development, 6(2), 219–231.
Hattie, J. (2012). Visible learning for teachers: Maximizing impact for learning. New York: Routledge.
Hattie, J.A.C. (2009). Visible learning: A synthesis of over 800 meta- analyses relating to achievement. London, UK: Routledge.
Heritage, M. (2007). Formative assessment: What do teachers need to know and do? Phi Delta Kappan, 89(2), 140–145.
Herman, J.L., Aschbacher, P.R., & Winter, L. (1992). A practical guide to alternative assessment. Alexandria, VA: Association for Supervision and Curriculum Development (ASCD).
Hettich, P. (1976). The journal: An autobiographical approach to learning. Teaching of Psychology, 3(2), 60–63.
Hibbard, M. (1996). A teacher’s guide to performance-based learning and assessment. Alexandria, VA: ASCD.
Hiebert, J. (1999). Relationships between research and the NCTM standards. Journal for Research in Mathematics Education, 30(1), 3–19.
Hiebert, J., Carpenter, T.P., Fennema, E., Fuson, K., Human, P., Murray, H., Olivier, A., & Wearne, D. (1996). Problem solving as a basis for reform in curriculum and instruction: The case of mathematics. Educational Researcher, 25(4), 12–21.
Hiebert, J., Gallimore, R., Garnier, H., Givvin, K.B., Hollingsworth, H., Jacobs, J., et al. (2003). Teaching mathematics in seven countries: Results from the TIMSS 1999 video study (NCES 2003-013). Washington, DC: U.S. Department of Education, National Center for Education Statistics.
Hiebert, J., & Grouws, D. A. (2007). The effects of classroom mathematics teaching on students’ learning. Second handbook of research on the teaching and learning of mathematics. Reston, VA: National Council of Teachers of Mathematics.
Hiebert, J., Morris, A. K., Berk, D., & Jansen, A. (2007). Preparing teachers to learn from teaching. Journal of Teacher Education, 58(1), 47–61.
Hiebert, J., & Wearne, D. (1993). Instructional tasks, classroom discourse, and students’ learning in second-grade arithmetic. American Educational Research Journal, 30(2), 393–425.
Hill, M., Sharma, M., O’Byrne, J., & Airey, J. (2014). Developing and evaluating a survey for representational fluency in science. International Journal of Innovation in Mathematics and Science Education, 22(6). Retrieved from: https://openjournals.library.sydney.edu.au/index.php/CAL/article/view/7484
Hufferd-Ackles, K., Fuson, K. C., & Sherin, M. G. (2004). Describing levels and components of a Math-Talk Learning Community. Journal for Research in Mathematics Education, 35(2), 81–116.
Hufferd-Ackles, K., Fuson, K. C., & Sherin, M. G. (2015). Describing levels and components of a Math-Talk Learning Community. In E. A. Silver & P. A. Kenney (Eds.), More lessons learned from research: Volume 1: Useful and usable research related to core mathematical practices, (pp. 125–134). Reston, VA: NCTM.
Hyde, A. (2006). Comprehending math: Adapting reading strategies to teach mathematics K-6. Portsmouth, NH: Heinemann.
Jerald, C. D. (2001). Dispelling the myth revisited. Washington DC: Education Trust. Johnson, C. I., & Mayer, R. E. (2009). A testing effect with multimedia learning. Journal of Educational Psychology, 101(3), 621–629.
Kapur, M. (2010). Productive failure in mathematical problem solving. Instructional Science, 38(6), 523–550.
Karweit, N., & Wasik, B. (1996). The effects of story-reading programs on literacy and language development of disadvantaged preschoolers. Journal of Education for Students Placed At-Risk, 4, 319–348.
Ketterlin-Geller, L. R., Chard, D. J., & Fien, H. (2008). Making connections in mathematics: Conceptual mathematics intervention for low-performing students. Remedial and Special Education, 29(1), 33–45.
Ketterlin-Geller, L. R., & Yovano , P. (2009). Diagnostic assessments in mathematics to support instructional decision making. Practical Assessment, Research & Evaluation, 14(16), 1–11.
Klibanoff, R. S., Levine, S. C., Huttenlocher, J., Vasilyeva, M., & Hedges, L. V. (2006). Preschool children’s mathematical knowledge: The effect of teacher ‘math talk.’ Developmental Psychology, 42(1), 59–69.
Kovalik, S. (1994). Integrated thematic instruction: The model. Kent, WA: Susan Kovalik & Associates.
Krebs, A. (2005). Analyzing student work as a professional development activity. School Science and Mathematics, 105(8), 402–411.
Lane, S. (2013). Performance assessment. In J.H. McMillan (Ed.), SAGE handbook of research on classroom assessment (pp. 313-329). Thousand Oaks, CA: Sage.
Lappan, G., & Briars, D. (1995). How should mathematics be taught? In I. M. Carl (Ed.), Seventy-five years of progress: Prospects for school mathematics (pp. 115-156). Reston, VA: National Council of Teachers of Mathematics.
Lauer, P. A., Snow, D., Martin-Glenn, M., VanBuhler, R. J., Stoutemeyer, K., & Snow-Renner, R. (2005). The influence of standards on K-12 teaching and learning: A research synthesis. Aurora, CO: Mid-Continent Research for Education and Learning.
Leinwand, S., & Fleischman, S. (2004). Teach mathematics right the first time. Educational Leadership, 62(1), 88–89.
Lembke, E., & Foegen, A. (2005). Identifying indicators of early mathematics proficiency in kindergarten and Grade 1. (Technical Report No. 6). Minneapolis: University of Minnesota. College of Education and Human Development. Retrieved from: www.progressmonitoring.org...
Lesh, R., Post T., & Behr, M. (1987). Representations and translations among representations in mathematics learning and problem solving. In C.J. Janvier (Ed.), Problems of representation in the teaching and learning of mathematics (pp.33–40). Hillsdale, NJ: Erlbaum.
Levasseur, K.& Cuoco, A. (2009). Mathematical habits of mind. In Teaching mathematics through problem solving, (pp.34–35). NCTM: Reston, VA.
Lo Cicero, A., Fuson, K.C., & Allexaht-Snider, M. (1999). Making a difference in Latino children’s math learning: Listening to children, mathematizing their stories, and supporting parents to help children. In L. Ortiz-Franco, N.G. Hernandez, & Y. De La Cruz (Eds.), Changing the faces of mathematics: Perspectives on Latinos (pp.59–70). Reston, VA: National Council of Teachers of Mathematics.
López, O.S. (2010). The digital learning classroom: Improving English language learners’ academic success in mathematics and reading using interactive whiteboard technology. Computers & Education, 54(4), 901–915.
Loveless, T. (2011). The 2010 Brown Center report on American education: How well are American students learning? With sections on international tests, who’s winning the real race to the top, and NAEP and the Common Core State Standards. Volume II, Number 5. Brown Center on Education Policy at Brookings.
Ma, L. (2010). Knowing and teaching elementary mathematics: Teachers’ understanding of fundamental mathematics in China and the United States. 2nd ed. New York: Routledge.
Marshall, A.M., Castro Superfine, A., & Canty, R. (2010). The case of Ms. Beyer: One teacher’s strategies for making connections among representations in a first-grade classroom. Teaching Children Mathematics, 7(1), 38–47.
Martin, T., Lukong, A., & Reaves, R. (2007). The role of manipulatives in arithmetic and geometry tasks. Journal of Education and Human Development, 1(1), online. Retrieved from: http://www.scientificjournals....
Marzano, R. (2000). What works in classroom instruction. Alexandria, VA: ASCD.
Marzano, R. (2009). Designing and teaching learning goals and objectives: Classroom strategies that work. Bloomington, IN.: Marzano Research Laboratory.
Marzano, R. (2013). The Marzano Teacher Evaluation Model. Bloomington, IN: Marzano Research Laboratory.
Marzano, R.J., Pickering, D., & McTighe, J. (1993). Assessing student outcomes: Performance assessment using the dimensions of learning model. Alexandria, VA: Association for Supervision and Curriculum Development.
Marzano, R.J., Pickering, D.J., & Pollock, J.E. (2001). Classroom instruction that works: Research-based strategies for increasing student achievement. Alexandria, VA: Association for Supervision and Curriculum Development (ASCD).
Matsumura, L.C., Slater, S.C., Junker, B., Peterson, M., Boston, M., Steele, M., et al. (2006). Measuring reading comprehension and mathematics instruction in urban middle schools: A pilot study of the instructional quality assessment. (CSE Technical Report 691). Los Angeles: University of California-Los Angeles. National Center for Research on Evaluation. Retrieved from: https://www.cse.ucla.edu/produ...
Mayer, R.E. (2002). Rote versus meaningful learning. Theory into Practice, 41, 226–233.
McDaniel, M.A., Roediger, H.L., & McDermott, K.B. (2007). Generalizing test-enhanced learning from the laboratory to the classroom. Psychonomic Bulletin & Review, 14(2), 200–206.
McGuire, P., Kinzie, M.B., & Berch, D.B. (2012).Developing number sense in Pre-K with five-frames. Early Childhood Education Journal, 40(4), 213–222.
Mellard, D.F., & Johnson, E.S. (2008). RTI: A practitioner’s guide to implementing response to intervention. Thousand Oaks, CA: Corwin Press.
Michaels, S., O’Connor, C., & Resnick, L. (2008). Deliberative discourse idealized and realized: Accountable talk in the classroom and in civic life. Studies in Philosophy and Education, 27(4), 283–297.
Mid-Continent Research for Education and Learning (McREL). (2010). What we know about mathematics teaching and learning, third edition. Bloomington, IN: Solution Tree Press.
Miri, B., David, B-C., & Uri, Z. (2007). Purposely teaching for the promotion of higher-order thinking skills: A case of critical thinking. Research in Science Education, 37(4), 353–369.
Morrow, L.M. (1988). Young children’s responses to one-to-one reading in school settings. Reading Research Quarterly, 23, 89–107.
Moskal, B. (2000). Understanding student responses to open- ended tasks. Mathematics Teaching in the Middle School, 5(8), 500–505.
Moss, C.M. (2013). Research on classroom summative assessment. In J.H. McMillan (Ed.), SAGE handbook of research on classroom assessment (pp.235–255). New York, NY: Sage Publications, Inc.
National Center for Education Statistics, U.S. Department of Education. (2015). The Nation’s Report Card: 2015 NAEP Reading and Mathematics Assessments. Retrieved online: https://www.nationsreportcard....
National Council of Teachers of Mathematics. (2000, 2009). Principles and standards for school mathematics. Reston, VA: Author. Retrieved from: http://www.nctm.org/standards/...
National Council of Teachers of Mathematics (NCTM). (2010). Focus in kindergarten. Reston, VA: Author.
National Council of Teachers of Mathematics. (2014). Principles to actions: Ensuring mathematical success for all. Reston, VA: Author.
National Council of Teachers of Mathematics. (2015). Access and equity in mathematics education. Reston, VA: Author. Retrieved from: http://www.nctm.org/Standards-...
National Council of Teachers of Mathematics. (2015). Intervention. Reston, VA: Author. Retrieved from: http://www.nctm.org/Standards-...
National Council of Teachers of Mathematics. (2014). Procedural fluency in mathematics: A position of the national council of teachers of mathematics. Retrieved from: https://www.nctm.org/uploadedF...
National Institute for Literacy. (2007). What content-area teachers should know about adolescent literacy. Washington, DC: NIL, NICHD.
National Mathematics Advisory Panel. (2008). Foundations for success: The final report of the National Mathematics Advisory Panel. Washington, DC: U.S.Department of Education. Retrieved from: http://www2.ed.gov/about/bdscomm/list/mathpanel/index.html
National Research Council. (1999). How people learn: Brain, mind, experience, and school. Washington, DC: National Academy Press.
National Research Council. (2001). Adding it up: Helping children learn mathematics. J. Kilpatrick, J. Swafford, & B. Findell (Eds.). Mathematics Learning Study Committee, Center for Education, Division of Behavioral and Social Science and Education. Washington, DC: National Academy Press. Retrieved from: http://www.nap.edu/ openbook.php?record_id=9822&page=1. doi:10.17226/9822
National Research Council. (2005). How students learn: Mathematics in the classroom. Washington, DC: National Academies Press. Retrieved from: http://www.nap.edu/openbook.ph...
National Research Council (2009). Mathematics learning in early childhood: Paths toward excellence and equity. C. T. Cross, T. A. Woods, & H. Schweingruber (Eds.). (2009). Washington, DC: National Academies Press. doi:10.17226/12519.
National Research Council. (2012). Education for life and work: Developing transferable knowledge and skills for the 21st century. Washington, DC: National Academies Press.
O’Neil, H. F., & Brown, R. S. (1998). Differential effects of question formats in math assessment on metacognition and affect. Applied Measurement in Education, 11(4), 331–351.
Partnership for 21st Century Skills. (2008). 21st century skills, education & competitiveness: A resource and policy guide. Tucson, AZ: Author. Retrieved from: http://www.p21.org/storage/doc...
Partnership for Assessment of Readiness for College and Careers. (2015). Mathematics test specifications documents. Retrieved from: http://www.parcconline.org/ mathematics-test-documents
Partnership for Learning. (2010). The impact of effective teachers and principals: Accelerating student performance by focusing on what matters most in our schools. Seattle, WA: Author. Retrieved from: http://www.partnership4learnin...
Pasquale, M. (2015). Productive struggle in mathematics. Interactive STEM Research Brief. Retrieved from: http://interactivestem.org/wp-...
Popham, W. J. (2006). All about accountability / phony formative assessments: Buyer beware. Educational Leadership, 64(3), 86–87.
Popham, W. J. (2008). Transformative Assessment. Alexandria, VA: Association for Supervision and Curriculum Development.
Rittle-Johnson, B., & Alibali, M. W. (1999). Conceptual and procedural knowledge of mathematics: Does one lead to another? Journal of Educational Psychology, 91(1), 175–189.
Rittle-Johnson, B., Siegler, R. S., & Alibali, M. W. (2001). Developing conceptual and procedural skill in mathematics: An iterative process. Journal of Educational Psychology, 93(2), 346–362.
Roediger, H. L., & Karpicke, J. D. (2006). The power of testing memory: Basic research and implications for educational practice. Perspectives on Psychological Science, 1, 181–210.
Rohrer, D. (2009). The effects of spacing and mixed practice problems. Journal for Research in Mathematics Education, 40(1), 4–17.
Rosenshine, B. (2012). Principles of instruction: Research-based strategies that all teachers should know. American Educator, Spring, 12–39.
Russell, S. J. (2000). Developing computational fluency with whole numbers. Teaching Children Mathematics, 7(3), 154–158.
Russo, M., Hecht, D., Burghardt, M.D., Hacker, M., & Saxman, L. (2011). Development of a multidisciplinary middle school mathematics infusion model. Middle Grades Research Journal, 6(2), 113–128.
Sarama, J., & Clements, D.H. (2002). Design of microworlds in mathematics and science education. Journal of Educational Computing Research, 27(1&2), 1–6.
Sarama, J., & Clements, D.H. (2006). Mathematics, young students, and computers: Software, teaching strategies, and professional development. The Mathematics Educator, 9(2), 112–134.
Sarama, J., & Clements, D.H. (2009). Early childhood mathematics education research: Learning trajectories for young children. New York: Routledge.
Schmidt, W.H., Houang, R., & Cogan, L. (2002). A coherent curriculum: The case of mathematics. American Educator, 26(2), 10–26.
Schmidt, W.H., Wang, H.C., & McKnight, C.M. (2005). Curriculum coherence: An examination of U.S. mathematics and science content standards from an international perspective. Journal of Curriculum Studies, 37, 525–559.
Schneider, M.C. (2007). National Assessment of Educational Progress: Mapping 2005 state proficiency standards onto the NAEP scales. Washington, DC: IES National Center for Education Statistics.
Schneider, M.C., Egan, K.L., & Julian, M.W. (2013). Classroom assessment in the context of high-stakes testing. In J.H. McMillan (Ed.), SAGE handbook of research on classroom assessment (pp.55–70).Thousand Oaks, CA: Sage.
Shannon, G.S., & Bylsma, P. (2003). Nine characteristics of high-performing schools: A research-based resource for school leadership teams to assists with the School Improvement Process. Olympia, WA: Office of the School Superintendent of Public Instruction.
Shadish, W.R., Cook, T.D., & Campbell, D.T. (2002). Experimental and Quasi-Experimental Designs for Generalized Causal Inference. Boston, MA, US: Houghton, Mifflin and Company.
Shepard, L.A. (2000). The role of assessment in a learning culture. Educational Research, 29(7), 4–14.
Sherin, B., & Fuson, K. (2005). Multiplication strategies and the appropriation of computational resources. Journal for Research in Mathematics Education, 36(4), 347–395.
Skiba, R., Magnusson, D., Marston, D., & Erickson, K. (1986). The assessment of mathematics performance in special education: Achievement tests, proficiency tests, or formative evaluation? Minneapolis: Special Services, Minneapolis Public Schools.
Smith, E.S., & Johnson, L.A. (2011). Response to intervention in middle school: A case story. Middle School Journal, 42(3), 24–32.
Smith, M.S., & Stein, M.K. (2011). Five practices for orchestrating productive mathematics discussions. Resnick, VA: Author.
Star, J.R. (2005). Reconceptualizing conceptual knowledge. Journal for Research in Mathematics Education, 36(5), 404–411.
Stein, M.K., & Lane, S. (1996). Instructional tasks and the development of student capacity to think and reason: An analysis of the relationship between teaching and learning in a reform mathematics project. Educational Research and Evaluation, 2(1), 50–80.
Stetson, R., Stetson, E., & Anderson, K.A. (2007). Differentiated instruction, from teachers’ experiences. The School Administrator, 8(64), online.Retrieved from: http://www.aasa.org/SchoolAdmi...
Stylianou, D. A. (2011). An examination of middle school students’ representation practices in mathematical problem solving through the lens of expert work: Towards an organizing scheme. Educational Studies in Mathematics, 76, 265−280.
Stylianou, D. A., & Silver, E. A. (2004). The role of visual representations in advanced mathematical problem solving: An examination of expert-novice similarities and differences. Mathematical Thinking and Learning, 6(4), 353–387.
Thompson, P. W., & Lambdin, D. (1994). Research into practice: Concrete materials and teaching for mathematical understanding. Arithmetic Teacher, 41(9), 556–558.
Thomson, S., Rowe, K., Underwood, C., & Peck, R. (2005). Numeracy in the early years: Project Good Start. Retrieved from: https://research.acer.edu.au/t...
Tomlinson, C. A. (2005). Traveling the road to differentiation in staff development. Journal of Staff Development, 26, 8–12.
Tomlinson, C.A. (1997). Meeting the needs of gifted learners in the regular classroom: Vision or delusion? Tempo, 17(1), 1, 10–12
Tomlinson, C.A. (1999). The differentiated classroom: Responding to the needs of all learners. Alexandria, VA: Association for Supervision and Curriculum Development.
Tomlinson, C.A. (2000). Reconcilable differences: Standards-based teaching and differentiation. Educational Leadership, 58, 6–13.
Tomlinson, C. A. (2005). Traveling the road to differentiation in staff development. Journal of Staff Development, 26, 8–12.
Tomlinson, C. A., & Allan, S. D. (2000). Leadership for differentiating schools and classrooms. Alexandria, VA: ASCD.
Tripathi, P. N. (2008). Developing mathematical understanding through multiple representations. Mathematics Teaching in the Middle School, 13(8), 438–445.
Underwood, B. J. (1961). Ten years of massed practice on distributed practice. Psychological Review, 68(4), 229–247.
Vygotsky, L. S. (1978). Mind in society: The development of higher psychological processes. Cambridge, MA: Harvard University.
Webb, D. C., Boswinkel, N., & Dekker, T. (2008). Beneath the tip of the iceberg: Using representations to support student understanding. Mathematics Teaching in the Middle School, 14(2), 110–113.
Weiss, I. R., & Pasley, J. D. (2004). What is high-quality instruction? Educational Leadership, 61(5), 24–28.
Wenglinsky, H. (1998). Does it compute? The relationship between educational technology and student achievement in mathematics. Princeton, NJ: Educational Testing Service Policy Information Center. Retrieved from: http://www.ets.org/research/po...
Wenglinsky, H. (2002). How schools matter: The link between teacher classroom practices and student academic performance. Education Policy Analysis Archives, 10(12).
Wenglinsky, H. (2006). Technology and achievement: The bottom line. Educational Leadership, 63(4), 29–32.
Williams, K. M. (2003). Writing about the problem-solving process to improve problem-solving performance. Mathematics Teacher, 96(3), 185–187.
Williams, L. (2008). Tiering and scaffolding: Two strategies for providing access to important mathematics. Teaching Children Mathematics, 14(6), 324–330.
Wise, A. (1989). Professional teaching: A new paradigm for the management of education. In T.J. Sergiovanni & J.H. Moore (Eds.), Schooling for tomorrow, Boston, MA: Allyn and Bacon. (pp.301–310)
Warshauwer, H. (2015). Productive struggle in middle school mathematics classrooms. Journal of Mathematics Teacher Education, 18(4), 375–400.
Wenglinsky, H. (2002). How schools matter: The link between teacher classroom practices and student academic performance. Education Policy Analysis Archives, 10(12).
Wiliam, D. (2011). Embedded formative assessment. Bloomington, IN: Solution Tree Press.
Williams, L. (2008). Tiering and scaffolding: Two strategies for providing access to important mathematics. Teaching Children Mathematics, 14(6), 324–330.
Yeager, D., Paunesku, D., Walton, G., & Dweck, C. (2013). How can we instill productive mindsets at scale?: A review of the evidence and an R&D agenda. A white paper prepared for the White House meeting: Excellence in Education: The Importance of Academic Mindsets.
Zechmeister, E., & Nyberg, S. (1982). Human memory: An introduction to research and theory. Monterey, CA: Brooks/Cole.
Zimmerman, B.J.(2001).Theories of self-regulated learning and academic achievement: An overview and analysis. In B.J. Zimmerman & D.H. Schunk (Eds.), Self-regulated learning and academic achievement: Theoretical perspectives (pp.1–65).Mahwah, NJ: Erlbaum.








