
Introducing the Concept
Too often, math is seen as a series of procedures. Do these steps. Draw it this way. Check your work. But lurking behind these procedures is the why. To be successful in math, it is not enough to merely memorize steps. It is critical to understand why those steps work.
Consider division. Long division is a thorn in the side of many math students (and teachers). The procedure is complicated, and people do it different ways. Once you learn the procedure, dividing 3,800 by 6 isn’t so bad. But dividing 3,801.72 by 5.993 is a nightmare:
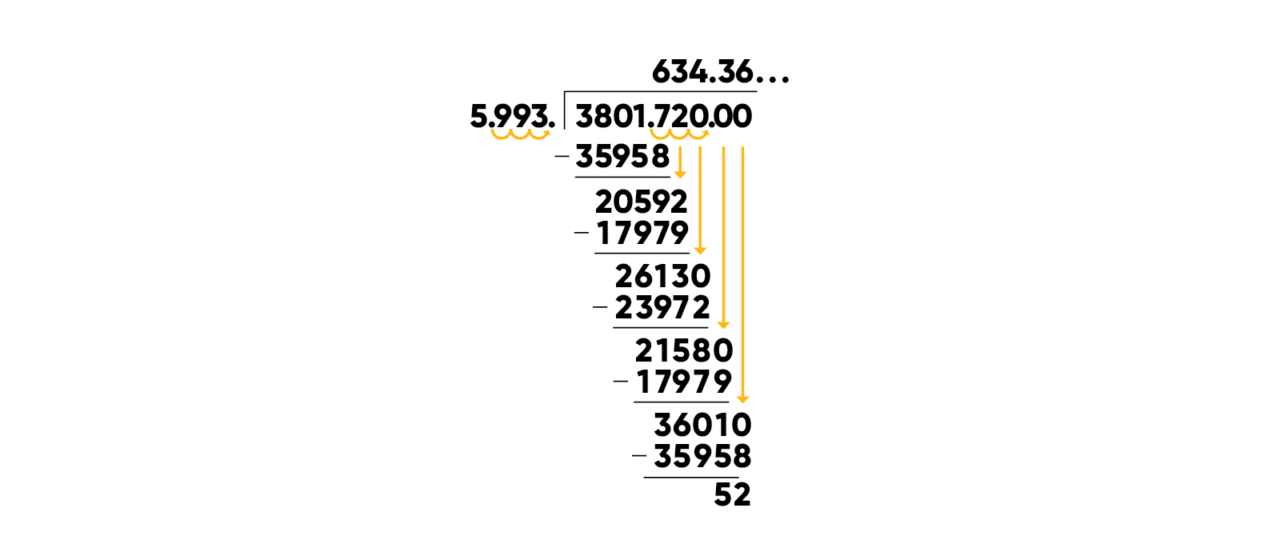
A conceptual understanding of division allows the learner to navigate the process more quickly and check reasonableness along the way. A student comfortable with multiplication understands that one can multiply both the dividend and divisor by 1,000 without changing the problem, thereby turning it into the slightly more manageable 380,172,000 ÷ 5,993.
A firm conceptual understanding of division has the potential to simplify the problem drastically. If estimating is sufficient, then realizing that 3,801.72 is close to 3,800, and that 5.993 is close to 6 turns a nightmarish procedure into a calculation that many people can work out mentally. No matter how one approaches the problem, having a conceptual grasp of division makes it clear that the quotient is somewhere around 600, and that a result of, say, over 60,000 is wildly off the mark.
What Is Conceptual Understanding?
Conceptual understanding broadly refers to a deep and integrated grasp of related ideas. However, it is ultimately a hard-to-define construct that applies to mathematics as much as any other domain, such as history or language. According to the seminal 2001 work Adding It Up by the National Research Council, there is no one term that “captures completely all aspects of expertise, competence, knowledge, and facility in mathematics.” Rather, mathematical proficiency can be thought of as having five strands that must be learned and practiced in tandem with one another:
- Conceptual understanding
- Procedural fluency
- Strategic competence
- Adaptive reasoning
- Productive disposition
In this light, conceptual understanding is a strand of achieving mathematical proficiency that involves making sense of the main ideas of mathematics. Conceptual understanding and procedural fluency are particularly interconnected and often the first components to develop. This relationship is discussed in our own Math in Focus research evidence base, where mathematics learning is described as occurring when students “develop an understanding of the relationships between and among concepts and between concepts and procedures.” When students understand a mathematical concept, they can see their knowledge as part of a coherent whole.
Conceptual Understanding in Math: Definition
Conceptual understanding in mathematics broadly refers to knowing more than isolated facts and methods and seeing a bigger picture of which facts and methods are a part. Students with conceptual understanding of mathematics can apply and adapt prior knowledge to new tasks, in effect making math applicable beyond solving just a single math problem.
Again, it is useful to compare conceptual understanding to procedural fluency. In the long division example that started this article, procedural fluency represents the arithmetic operations that result in a correct quotient, whereas conceptual understanding represents how the individual calculations are seen as part of an overarching division problem, or perhaps even the sense of knowing when that particular division would be needed to solve another problem. Procedures can often be taught quickly and practiced repeatedly. Conceptual understanding, on the other hand, unfolds over time—across years and a lifetime.
Why Do Students Need to Learn Conceptual Understanding?
Mathematical understanding is not a linear path from A to B. Consider math problems like the following, all of which have multiple solutions that can be approached using different principles and procedures, but whose solutions require learning mathematical ideas deeply and flexibly:
- Reason abstractly and quantitatively: How do I save up and/or borrow enough money to afford college?
- Model with mathematics: What furniture would fit properly in a specific room?
- Look for and make use of structure: How should I identify and organize information about the inventory I have for my new store?
In all these cases, procedural fluency alone is not sufficient to solve the problems. Conceptual understanding of mathematics is also needed to tackle how each of these problems should be approached, along with what techniques and procedures are appropriate.
Conceptual understanding is also an important key to unlocking math performance in students who are behind in grade-level standards. Research indicates that students who lack understanding of underlying concepts respond better to interventions that explicitly teach the concept instead of focusing on arithmetic or procedural fluency.
Mathematics is deeply interconnected. Understanding why multiplication works in third grade can help a student multiply fractions in fifth grade, combine variables in sixth grade, evaluate functions in eighth grade, and operate with matrices in high school (to name a few examples). Trying to teach a huge number of skills in a short amount of time can feel overwhelming, if not impossible. But if you can reduce that number to a smaller list of underlying concepts, teaching those skills becomes achievable. It may feel silly to devote hours to discussing a few multiplication problems in third grade instead of, say, practicing a specific procedure hundreds of times, but those hours spent nurturing a deeper conceptual understanding pay dividends over time as students progress in their math learning.
How to Teach Conceptual Understanding
It is surely easier to describe what conceptual understanding is than it is to teach it! Formative assessment is important when evaluating how deeply a student understands a concept. Look for the evidence of this kind of understanding in students’ work and discussions. Begin by identifying whether they are struggling with a procedural skill (for example, correctly multiplying two numbers) or whether they are struggling to understand something more fundamental (for example, not realizing that two numbers are supposed to be multiplied).
If students are in fact struggling with a fundamental understanding, identify the critical concept(s) that the students need support with. To continue the previous example, this could be a basic understanding of what multiplication is and when to apply it. This support will benefit students throughout their math careers, especially those who have gaps in their math learning. Teaching for depth gives students an opportunity to master ideas, and they’ll be more likely to retain what they learned.
In order to cultivate critical thinking capacities in mathematics concepts, students need regular opportunities to be challenged by problem solving tasks, in particular tasks that have multiple paths to a solution. For this, there are a few tactics that promote the teaching of conceptual understanding systematically:
- Provide multiple ways to visualize and represent math so that students have options when trying to model a math problem. Our Math in Focus program in particular is designed to promote understanding using visual models.
- Use a variety of routine and nonroutine problems so that students can apply math flexibly to novel situations.
- Engage in classroom discussion about procedural skills so that students are using language to describe and reflect on math and evaluate why a procedure works.
Conceptual Understanding in Math Examples
Many examples of conceptual understanding can be found within our programs. HMH Into Math in particular is a student-centered K–8 math curriculum designed to build deep understanding of mathematical ideas. The Spark Your Learning activities that begin each lesson are designed to pique students’ curiosity, explore math concepts, and connect them to procedures. One example involving division is provided below, with additional examples in our blog posts on estimating length and collecting data.

There are other ways to build conceptual understanding within Into Math. There are entire “Build Understanding” lessons that are designed to promote conceptual understanding. Additionally, the progression of lessons across a module is crafted so that students are deepening their conceptual understanding as they complete them.
No matter what math curriculum you’re using, you can always find examples of conceptual understanding. Look for activities and tools that let students invent, manipulate, and explore different ways of visualizing a concept. Discourse is also important, as it helps students put their thoughts into words and compare their thinking with others. There are plenty of tools, such as guided questions and sentence frames, to help facilitate discourse.
The Benefits of Conceptual Understanding
Conceptual understanding is difficult to teach, far moreso than teaching straightforward procedures, like the standard algorithm for multiplication. The teacher must possess a deep background in the content, not only to recognize when students lack conceptual understanding, but also to know which tools would best remedy the problem. This is no easy task and asks a lot of teachers, many of whom are already strapped for time or focused on meeting state assessment requirements.
However, the benefits of effectively teaching conceptual understanding are far-reaching. A student who knows a procedure, such as the standard algorithm for multiplication, has the tools needed to multiply two numbers. But when a student knows a concept behind multiplication, then they are ready to apply multiplication to any problem they’re faced in life.
***
Explore HMH’s innovative and research-based solutions to help your students develop conceptual understanding in your math classroom.
Get our free guide full of research-backed information.












