At a glance
- Program: Math in Focus®: Singapore Math® by Marshall Cavendish®
- Subject: Math
- Report Type: Research Evidence Base
- Grade Level: Elementary, Middle
Math in Focus®: Singapore Math® by Marshall Cavendish® is an innovative mathematics program for Grades K–8 + Accelerated that focuses on problem solving and the use of model drawing to drive the acquisition and application of mathematical skills.
The principles underlying Math in Focus are built on the solid base of extensive research that supports the Singapore Math® framework. The Singapore Math® method from which the program originates is based on research of math mastery in Singapore, which consistently ranks at the top in international math testing. The intentional progression of concepts in the Singapore Math® approach instills a deep understanding of mathematics. An attitude that math is important, approachable, and is also essential. Students perform at a higher level when their potential for understanding and success is assumed.
This research base document cites the extensive literature on mathematics pedagogy and learning as it relates to the key features and philosophy of Math in Focus.
The instructional pathway throughout the chapters within Math in Focus provides an effective, blended learning experience for small-group and whole-class implementations. The different features and sections in each chapter help students build conceptual understanding through a range of practice and fluency-building activities, as well as frequent opportunities for classroom discussion, timely differentiated math instruction, and problem solving. Chapter Planning Guides, in the Teacher’s Edition, show in detail how each section can be carried out daily.

In Singapore, mathematics is taught in an innovative way, with an emphasis on problem solving. This has not always been the case, though. Prior to 1980, the country imported all of its mathematics instructional content from other nations. Beginning in 1980, Singapore launched a new approach to mathematics instruction and the Curriculum Development Institute of Singapore (CDIS) was established. One charge of CDIS was to develop primary and secondary textbooks for the country. At the same time, the Ministry of Education, the centralized education authority in Singapore, set new goals for mathematics education. These goals emphasized a focus on problem solving and on heuristic model drawing. The CDIS incorporated these goals into textbooks, and in 1982 the first Singapore math program, Primary Mathematics 1–6, was published.
The impact of Singapore’s curricular and instructional initiatives is evidenced by the dramatic improvements in math proficiency for Singapore students on international assessments. In 1984, Singapore’s students were placed 16th out of 26 nations in the Second International Science Study (SISS). By 1995, however, the Trends in International Mathematics and Science Study (TIMSS) ranked Singapore’s students first among participating nations. TIMSS is administered every four years.
Since 1995, Singapore scored first in both 4th and 8th grades on TIMSS in 1999 and 2003 and in the top three in 2007. In the most recent administration of TIMSS, 2015, Singapore ranked first in mathematics at both Grades 4 and 8, and continued its upward trend on the country’s average scale score (Mullis, Martin, Foy, & Hooper, 2016).
For the past two decades, math educators around the world have been interested in the secret of Singapore’s success. While many factors have been catalogued—a coherent national curriculum, teacher training, a public belief in the importance of math to the national economy—without fail, all descriptions emphasize the importance of problem solving in the Singapore curriculum (Ginsberg, Leinwand, Anstrom, & Pollock, 2005; Fan & Zhu, 2007).
Singapore has scored at the top in results for the Trends in International Mathematics and Science Study (TIMSS) for Grade 4 and Grade 8 for over 20 years while the United States has been surpassed internationally in its mathematics performance. In the most recent results from 2015 for TIMSS, U.S. fourth-graders ranked 15th and eighth-graders ranked 12th (National Center for Education Statistics [NCES], 2017, p. 5).
Experts frequently attribute Singapore’s success in mathematics to the country’s strong emphasis on problem solving. In an exploratory study comparing key features of the Singapore and U.S. mathematics systems in the primary grades, Ginsberg et al. (2005) found that a major reason why Singaporean students were more successful than their U.S. counterparts is because their country’s mathematics textbooks build deep understanding of concepts through multistep problems and concrete illustrations that demonstrate how abstract mathematical concepts are used to solve problems from different perspectives.
The National Council of Teachers of Mathematics (NCTM®) has extended and elaborated on the guiding mathematics principles (2000) in its 2014 publication Principles to Actions: Ensuring Mathematical Success for All. These principles are based on more than a decade of research and experience and continue to be a driving force behind a high-quality mathematics education for all students. NCTM guidelines are supported within Math in Focus.
Mathematics goals are focused, purposeful, and coherent. Each section clearly outlines the standards and practices, objectives, and learning progressions so teachers can best support and focus student learning. Identifying and clarifying what students are expected to learn and understand in a mathematics classroom is an essential component to success (Wiliam, 2011). Teachers and students benefit from establishing a shared foundation of what is being learned and why it is important to learn. “Formulating clear, explicit learning goals sets the stage for everything else” (Hiebert, Morris, Berk, & Jansen, 2007, p. 57).
Tasks require a high level of cognitive demand, which is necessary when promoting reasoning and problem solving in the mathematics classroom. In a study that compared students exposed to teaching strategies that promoted higher-order thinking with those who were taught more traditionally, researchers found that experimental group students outperformed control group students, showing significant improvement in their critical thinking skills: “Our findings suggest that if teachers purposefully and persistently practice higher order thinking strategies for example dealing in class with real-world problems, encouraging open-ended class discussions, and fostering inquiry-oriented experiments, there is a good chance for a consequent development of critical thinking capabilities” (Miri, David, & Uri, 2007, p. 353). Student learning is greatest in classrooms where the tasks consistently encourage high-level student thinking and reasoning and least in classrooms where the tasks are routinely procedural (Boaler & Staples, 2008; Stein & Lane, 1996).
Connections among mathematical ideas are an essential part of mathematics learning. Making connections between new information and students’ existing knowledge—knowledge of other content areas and of the real world—has proved to be more effective than learning facts in isolation (Bransford, Brown, & Cocking, 2000; Caine & Caine, 1994). Further, connecting mathematics to science, social studies, and business topics can increase students’ understanding of and ability with mathematics (Russo, Hecht, Burghardt, & Saxman, 2011). Students maximize learning when they make connections among ideas, both within mathematics and outside of the mathematics content.
Students use mathematical models and representations to help make mathematical concepts more concrete to students. “Because of the abstract nature of mathematics, people have access to mathematical ideas only through the representations of those ideas” (National Research Council [NRC], 2001, p. 94). For young students, representations are especially important because they can be physical objects or actions they perform as they are trying to solve problems (NRC, 2001). As students create representations, they have the opportunity to internalize and process what they are doing, what they are creating, and what they are seeing, which in turn allows them to play an active role in their learning.
Students engage in mathematical discourse throughout each lesson. When students write about and discuss math concepts, they have the chance to think through, defend, and support their ideas. The process of encouraging students to verbalize their thinking—by talking, writing, or drawing the steps they used in solving a problem—has been shown to be consistently effective (Gersten, Clarke, & Mazzocco, 2007). Communicating about math improves learning; “encouraging students to verbalize their current understandings and providing feedback to the student increases learning” (Gersten & Chard, 2001, online).
“Effective teaching of mathematics uses purposeful questions to assess and advance student reasoning and sense making about important mathematical ideas and relationships” (NCTM, 2014). While types of questions vary from asking students to recall facts to requesting an explanation for an answer, presenting questions throughout the learning process is necessary to understanding how students are making sense of the math. As noted in research by Weiss and Pasley (2004), questions are critical in helping students make connections and learn important mathematics concepts—especially questioning that effectively gauges student understanding.
To achieve understanding, each section recognizes and supports the relationship between procedural fluency and conceptual understanding. Specifically, “Effective teaching of mathematics builds fluency with procedures on a foundation of conceptual understanding so that students, over time, become skillful in using procedures flexibly as they solve contextual and mathematical problems” (NCTM, 2014, p. 42). Effective mathematics instruction cannot have one without the other as “procedural knowledge and conceptual understandings must be closely linked” (Donovan & Bransford, 2005, p. 232).
Students have the opportunity to practice and engage in productive perseverance with mathematical problems and ideas that encourage them to think about their own thinking and to discover that learning can happen without rushing to simply find the correct answer. Teachers who guide students through this vital productive perseverance are supporting the development of student learning and understanding (Hiebert & Grouws, 2007). Students receive reassurance as they grapple with ideas, and teachers support them through the process rather than give them the answers (Hiebert et al, 1996).
Teachers are prompted to elicit and use evidence of student thinking. To discover what students know or don’t know, what they do well or poorly, the teacher must closely examine the students’ work. “Effective teaching of mathematics uses evidence of student thinking to assess progress toward mathematical understanding and to adjust instruction continually in ways that support and extend learning” (NCTM, 2014, p. 53).
Math in Focus provides a focused, coherent curriculum built upon a research-based framework that develops concepts, skills, processes, attitudes, and metacognition and emphasizes critical thinking and problem solving. Additional research has demonstrated the program’s efficacy. In a study that reviewed how the United States can learn from Singapore’s mathematics system, the authors found that “Singapore’s unique emphasis on multistep word problems, in particular, is consistent with its emphasis on promoting conceptual understanding through solving thoughtful problems” (Ginsberg et al., 2005, p. 35).
Mathematics learning is founded on students acquiring and applying a multitude of concepts and skills in order to solve a wide range of problems in varying nonroutine and real-world situations. According to the Singapore Ministry of Education’s Primary Mathematics Syllabus (2013):
“The Mathematics Framework has been a feature of our mathematics curriculum since 1990, and is still relevant to date. The central focus of the framework is mathematical problem solving, that is, using mathematics to solve problems. The framework sets the direction for and provides guidance in the teaching, learning, and assessment of mathematics at all levels, from primary to pre-university. It reflects also the 21st century competencies.” (p. 14)
“Singapore’s framework lays out a balanced set of mathematics priorities centered on problem solving. It includes an emphasis on computation skills along with more conceptual and strategic thinking”(Ginsberg et al., 2005, p. xi).
The effectiveness of such an approach is echoed by researchers and policy makers in the United States. The National Research Council (2001) and National Council of Teachers of Mathematics (2014) call for multipronged models for mathematics instruction that emphasize conceptual understanding, problem solving, strategic competence, procedural fluency and skill building, habits of mind, and metacognitive awareness.
“Neither concept development nor the development of problem solving abilities proceeds in the absence of the development of beliefs . . . and other components. . . . A fresh view of problem solving needs to view the learning of mathematics and problem solving as integrated, as largely based on modeling activity” (Lesh & Zawojewski, 2007, pp. 778–779).
“Mathematics learning in early childhood requires children to use several specific mathematical reasoning processes, also known as ‘big ideas,’ across domains. These big ideas are overarching concepts that connect multiple concepts, procedures, or problems within or across domains or topics and are a particularly important aspect of the process of forming connections” (Cross, Woods, & Schweingruber, 2009, p. 44).
While some see gaining knowledge and applying knowledge separately, problem solving is a bridge between the two that enables students to build understanding while applying skills and knowledge. “Students immersed in classroom experiences that let them engage in learning mathematics concepts through problem solving, making and using abstractions, and developing and applying mathematical theories have greater opportunities for developing mathematical habits of mind” (Bryant, 2015, online).
Problematizing content fosters understanding. “Treating mathematics as problematic is the most powerful and practical way to think about problem solving” (Hiebert et al., 1996, p. 18).
How Math in Focus Delivers
Each time a new concept is introduced in Math in Focus, problem solving is central. Students are taught specific problem-solving strategies in a carefully sequenced manner of concrete to pictorial to abstract.
Each section in Math in Focus develops students’ problem-solving abilities by building their conceptual understandings, skills, mathematical processes, attitudes toward math, and self-awareness.
- Concepts are developed by following an articulated sequence of concrete to pictorial to abstract.
- Concepts and skills are reinforced through opportunities to practice and apply.
- Carefully sequenced sections allow students to reach mastery—and build confidence—before moving on.
- Routine and nonroutine problems require that students solve each problem with a conscious awareness of how to approach problem solving.
- Guided Practice, Independent Practice, On Your Own, Hands-On activities, Let’s Explore, Math Journal, and Put On Your Thinking Cap! incorporate all components of the pentagon.
An effective mathematics curriculum incorporates rich and rigorous problem-solving tasks that are essential for developing mathematical understanding (David & Greene, 2007; NCTM, 2014).
The Singapore Ministry of Education has long identified problem solving as the primary goal of mathematics:
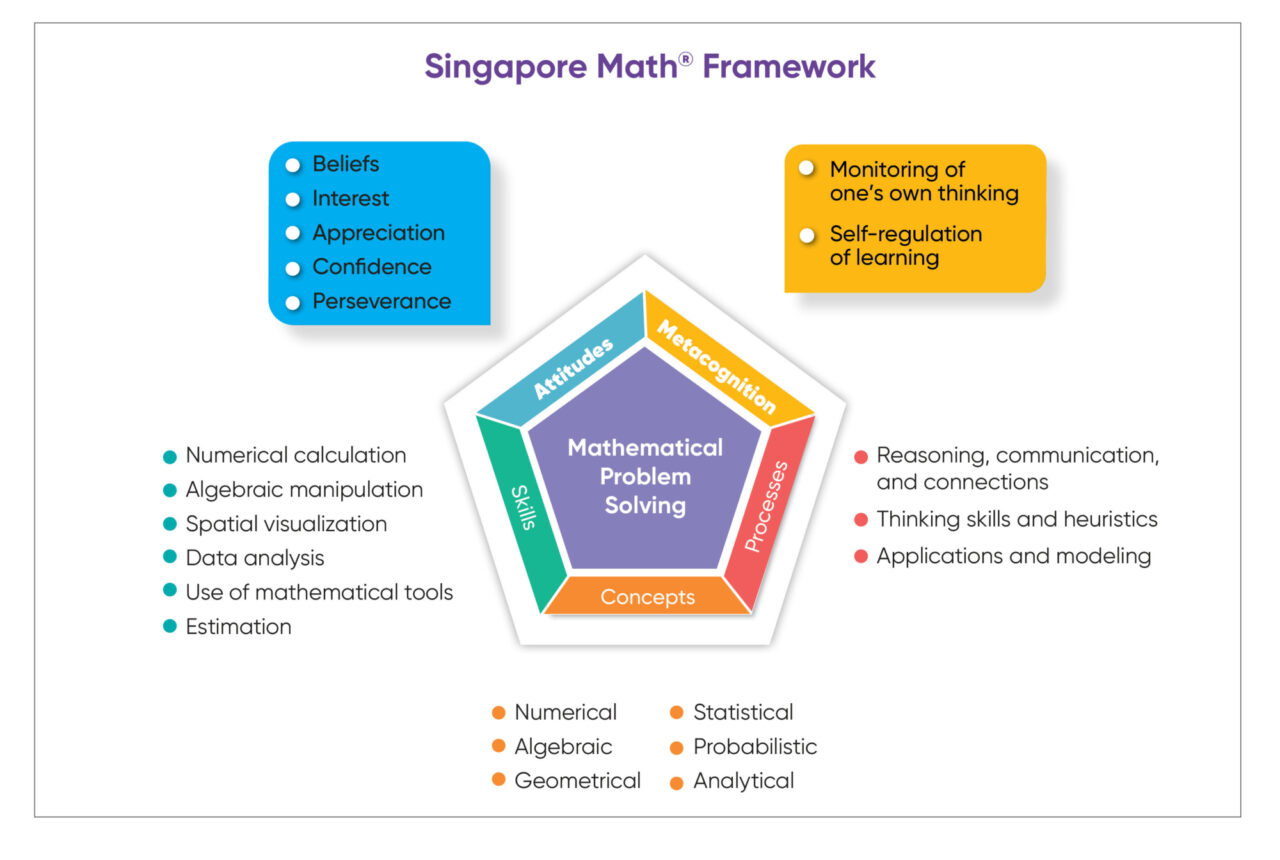
“Mathematical problem solving is central to mathematics learning. It involves the acquisition and application of mathematics concepts and skills in a wide range of situations, including non-routine, open-ended and real- world problems. The development of mathematical problem solving ability is dependent on five interrelated components, namely, Concepts, Skills, Processes, Attitudes and Metacognition.” (CPPD, 2006, online)
NCTM (2000) defines problem solving as “engaging in a task for which the solution method is not known in advance” (p. 52). Johnson, Herr, and Kysh (2004) define problem solving as “knowing what to do when you don’t know what to do” (p. 3). But perhaps the best definition comes from the math teacher who in the last century advanced problem solving into the math curriculum, George Polya. Polya (1965) said, “solving a problem means finding a way out of a difficulty, a way around an obstacle, attaining an aim which is not immediately attainable” (p. ix).
Singapore textbook writers have been familiar with Polya’s work and include it in manuals designed for teachers (Huat & Huat, 2006). In particular they cite the four-step model that Polya (1965) recommended: understand the problem, devise a plan, carry out the plan, and reflect on the solution. While this same structure is in many U.S. textbooks as well, it is the special attention that Singapore Math® pays to steps one and four that may set it apart. In the first step, students connect a problem to prior problems. In the reflection stage students consider alternate solutions and whether the method can be applied to other problems.
Singapore Math® instructional content builds on the work of Polya (1957) by teaching specific strategies for problem solving, what Polya called heuristics. Many heuristics—such as “look for a pattern,” “draw a picture,” “simplify the problem,” and “work backwards”—are included in U.S. math textbooks. But too often, U.S. texts teach these strategies by “type.” That is, students learn to “look for a pattern” and then are presented with problems that can be solved in that way. In Singapore, students are instead given a variety of nonroutine problems and encouraged to consider which strategy will work best for a particular problem.
Influenced by Polya and the belief that within mathematics instruction an emphasis on problem solving and an emphasis on understanding can have a mutually supportive relationship, Schroeder and Lester (1989) advocated for teaching about, for, and through problem solving with understanding being the focus and goal. These researchers note that instruction about problem solving entails a similar four phase process as well as use of heuristics advanced by Polya (and referenced above)—and a great deal of explicit instruction and discussion about how problems are solved. Instruction for problem solving focuses largely on application—students are given numerous instances of math structures and concepts under study followed by numerous opportunities to apply learning and to transfer what they learn from one problem context to another. Finally, contrastingly, in instruction through problem solving, the problems are valued as both the purpose for learning mathematics as well as the primary way of teaching mathematics. According to Schroeder and Lester (1989), instruction that combines all three approaches—about, for, and through problem solving—is most effective in helping students developing the means of generating their own deeper understandings of mathematics.
Within the Singapore Math® curriculum, there are 11 different heuristics or strategies that primary students are taught to apply in solving problems, which Math in Focus program author Ng Wee Leng (2008) categorizes into the following:
- Representation: diagrams, lists, models
- Calculated guess: guess and check, suppositions/assumptions, look for patterns
- Going through the problem: work backwards, act it out, before and after
- Modification: restate the problem, simplify the problem, solve part of the problem
Fong Ho Kheong, program consultant and author of Math in Focus, has found that some students have difficulty transitioning from the concrete model approach to the algebraic method as they progress through grade levels, resulting in them falling back on models learned in earlier schooling when encountering unfamiliar problems in advanced math. To effectively bridge the gap between primary and secondary mathematics, Fong (1993) advocates for a technique that combines features of both the model and algebraic methods of problem solving.
How Math in Focus Delivers
Mathematical problem solving is central to mathematics learning. Drawing on research by Polya (1957, 1965, & 1971) and Schroder and Lester (1989), Math in Focus has students learn for, about, and through problem solving in order to master concepts fully and apply them to nonroutine, open-ended, and real-world problems.
Math in Focus weaves problem solving throughout each lesson. The problems grow in difficulty from one-step, to two-step, to multistep, to nonroutine. Students are encouraged to discuss problems using unique approaches (Let’s Explore! and Put On Your Thinking Cap!), but are taught a systematic, strategic process for tackling problems using bar models. This helps students know where to start and to have a positive attitude about math problems in general as well as confidence in their own abilities to succeed. Math in Focus fosters a growth mindset.
The ability to think critically is essential in our 21st-century world; never before has the workplace demanded such complex levels of thinking and problem solving. To keep pace with a rapidly changing world and its known and unforeseen issues, our students need to be prepared for a future in mathematics. Mathematics is one means toward the desired end of critical thinking; to think in mathematically proficient ways is to think critically (Goldenberg et al., 2015).
Rigorous tasks require a high level of cognitive demand, which is necessary in the development of reasoning and problem solving. Mathematical learning is greatest in classrooms where the tasks consistently encourage high-level student thinking and reasoning and least in classrooms where the tasks are routinely procedural (Boaler & Staples, 2008; Stein & Lane, 1996).
Effective instructional programs build on children’s intuitive mathematical thinking and utilize current knowledge to help children learn to solve problems, employ strategies, and engage in complex thinking (Carpenter, Fennema, Franke, Levi, & Empson, 2015). Lacking calculation skills are not incompatible with higher-level understandings. Indeed, there is a consensus among experts that in the course of learning mathematics, all students, regardless of their backgrounds or level of expertise, need opportunities to participate in mathematical activities across a broad range of complexity. Mathematical proficiency requires that all students develop concepts and skills, become flexible with mathematical ideas, and engage in higher-order or critical thinking; rigorous content and expectations underpin such opportunities (Franke, Kazemi, & Battey, 2007; NCTM, 2014).
In a study comparing students exposed to teaching strategies that promoted higher-order thinking with those who were taught more traditionally, researchers found that experimental group students outperformed control group students, showing significant improvement in their critical thinking skills (Miri, David, & Uri, 2007).
Writing, such as in the form of journaling, is an effective means of building critical thinking in mathematics “Reflection and communication are intertwined processes in mathematics learning. . . . Writing in mathematics can also help students consolidate their thinking because it requires them to reflect on their work and clarify their thoughts about the ideas” (NCTM, 2000, p. 61). While they are writing, students can put concepts and procedures in their own words and reflect on learning that confuses them or makes sense to them. Students need opportunities to engage in academic discourse—and writing is an effective way. Journals can also provide additional support of effective instructional practices when students use them to go beyond note taking, to develop narrative statements and nonverbal representations (Marzano, Pickering & Pollack, 2001).
Numerous studies have emphasized the importance of writing in the mathematics classroom. David Pugalee (2005), who researches the relationship between language and mathematics learning, asserts that writing supports mathematical reasoning and problem solving and helps students internalize the characteristics of effective communication. He suggests that teachers read student writing for evidence of logical conclusions, justification of answers and processes, and the use of facts to explain their thinking. Bosse and Faulconer (2010) report that writing in the mathematics classroom results in deeper student learning. Importantly, writing appears to benefit all students, with researchers finding benefits for low-achieving students (Baxter, Woodward, & Olson, 2005) and high-achieving students (Brandenburg, 2002).
How Math in Focus Delivers
Math in Focus develops students’ abilities to think critically by providing opportunities for students to carry out investigative activities and discuss alternate solutions to open-ended routine and nonroutine problems. Critical thinking questions are woven throughout the program to promote productive struggle and creative problem solving.
Each Math in Focus chapter concludes with Put On Your Thinking Cap!, which challenges students to solve nonroutine questions by applying heuristics and higher-order thinking. These problems ask children to draw on deep prior knowledge as well as recently acquired concepts, combining problem-solving strategies with critical-thinking skills that include:
- Classifying
- Comparing
- Sequencing
- Analyzing parts and whole
- Identifying patterns and relationships
- Inductions (from specific to general)
- Deduction (from general to specific)
- Spatial visualization
The program’s Math Journal provides the objective of the question and states the required math habit or strategy. It invites students to record and reflect in their own words the mathematical concepts learned.
The concrete–pictorial–abstract (CPA) approach is a key instructional strategy for the development of primary mathematics concepts in Singapore (Hui, Hoe, & Lee, 2017). The CPA framework has an established theoretical basis deriving from Bruner (1966), who proposed that the learning sequence of a new mathematical concept follows a progression that begins with an experience from concrete actions undertaken or with concrete objects (enactive) that is then translated into perceptual images of the experience formed (iconic), subsequently leading to the adoption of the mathematical symbol. This theory was adapted into the concrete–representational–abstract (CRA) model and, in the form of the concrete–pictorial–abstract approach, has become an instructional heuristic advocated by the Singapore Ministry of Education since the early 1980s (Leong, Ho, & Cheng, 2015; Hui, Hoe, & Lee, 2017).
Empirical research has indicated both CRA and CPA are effective ways for students to develop understanding of math concepts. “Indeed, the use of CRA approach to teaching mathematics concepts, especially at the elementary level has been proven to be effective” (Leong, Ho, & Cheng, 2015, p. 3). Salingay and Tan (2018) found positive effects on both performance and retention for students that had utilized CPA when compared with the non-CPA group, leading researchers to recommend use of the CPA approach to enhance the learning for students. While the concrete to pictorial to abstract approach benefits all students, multiple studies have shown it to be particularly effective with students who have mathematics difficulties, mainly because it moves gradually from actual objects through pictures and then to symbols (Agrawal & Morin, 2016; Jordan, Miller, & Mercer, 1998; Sousa, 2008).
Other studies demonstrate the effectiveness of using concrete materials and pictorial representations when teaching students with learning disabilities, dyslexia, and other language difficulties; such research shows that these approaches successfully help students with learning disabilities master math concepts including algebra skills, basic math facts, coin sums, fractions, multiplication, and place value (Miller & Hudson, 2007).
Manipulatives can be a key element within a CPA approach. “A systematic way to integrate the use of manipulative devices and pictorial representations into explicit instruction designed to teach important concepts is through use of the concrete-representation-abstract (CRA) teaching sequence” (Miller & Hudson, 2007, p. 49). Here is one effective sequence: The teacher first illustrates the concept using manipulative devices. Representational pictures or tallies are then substituted for the manipulatives. Finally, instruction proceeds to the abstract level of problem solving without objects or representations. “When students connect manipulative models to their intuitive, informal understanding of concepts and to abstract symbols, when they learn to translate between representations, and when they reflect on the constraints of the manipulatives that embody the principles of a mathematics system . . . they build Integrated-Concrete ideas” (Clements, 1999, pp. 55–56).
How Math in Focus Delivers
Visual representation is a hallmark of Math in Focus. Powerful models are featured throughout program levels to build and extend conceptual understanding. Instruction consistently and progressively follows the sequence of moving students from concrete to pictorial to abstract.
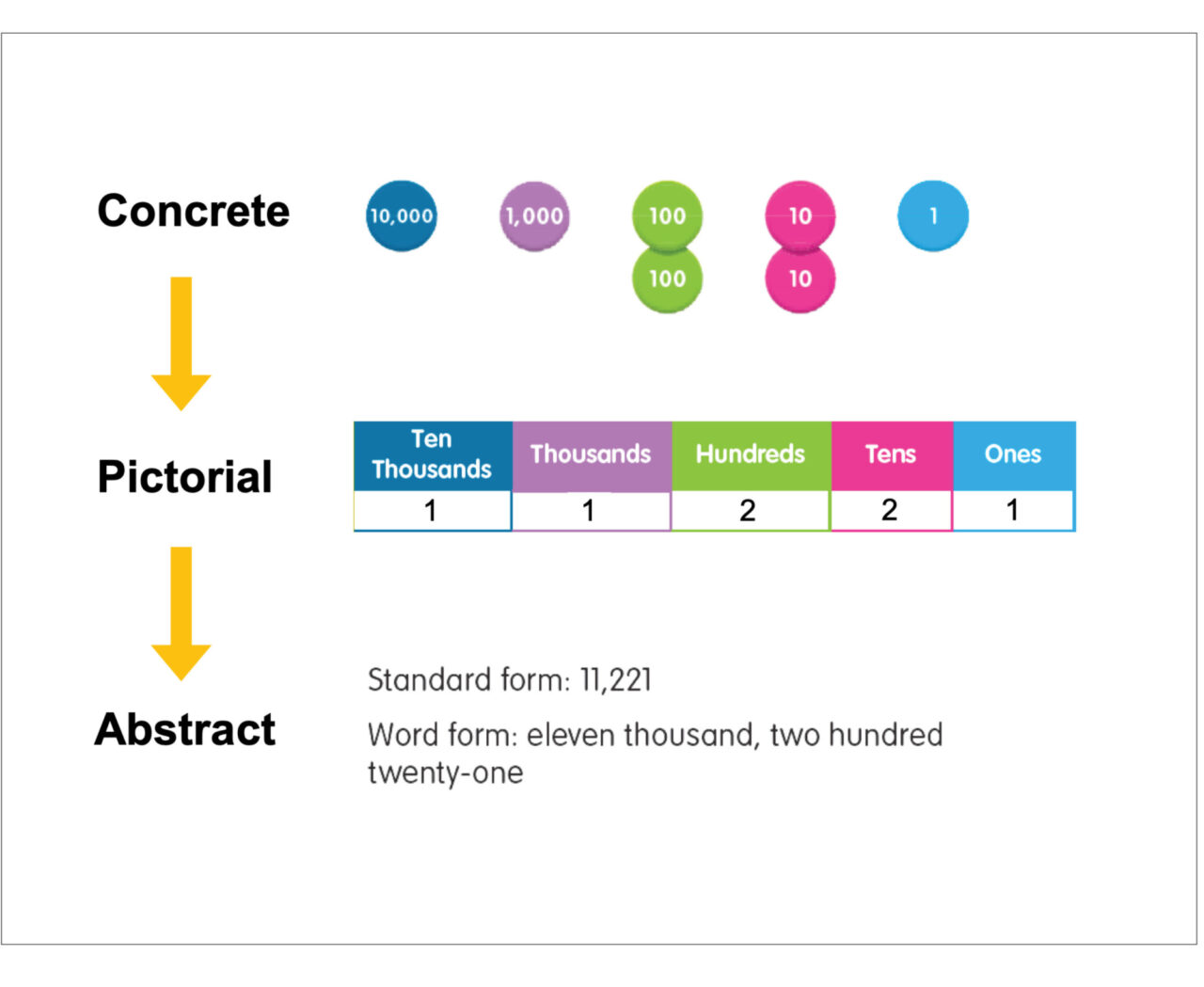
Visual models and representations help make abstract mathematical concepts more concrete to students as well as aid in the internalization of procedures for problem solving, increased creativity, greater metacognition, and students’ more active participation in their own learning (NRC, 2001). Dr. Yeap Ban Har of Singapore’s National Institute of Education attests to the effectiveness: “The use of ‘model method’ provides students with a means to handle information, deal with complexity, and at the same time, communicate their thinking through the use of visual models which they can manipulate” (2008, online).
One effective form of modeling in mathematics is bar modeling. Bar models are versatile and transferable tools that students can use to visualize a range of math concepts, such as fractions, ratios, percentages, and more, and both routine and nonroutine problems. Drawing bar models while solving word problems allows students to determine the knowns and unknowns in a given situation. Bar models extend the concrete–pictorial–abstract approach, especially the pictorial phase, as they allow students to illustrate mathematical information given in problems and prepare them to understand more complex math on a conceptual level. This method is most effective when used frequently as standard practice throughout the math curriculum.
Bar modeling, sometimes called model drawing, is the most famous and developed of the heuristics (strategies) taught in Singapore. Hoven and Garelick (2007) attribute some of the success of Singapore’s performance on international math exams to the country’s emphasis on problem solving using the bar model technique across grade-level progressions of difficulty. Bar models are introduced in Grade 2 with addition and subtraction problems. In later grades, students use them flexibly on more difficult, multistep problems. By grade 6, students are ready to solve complex problems and, with that solid foundation for both solving problems and representing symbolically, are prepared for algebraic reasoning and the study of algebra. Hoven and Garelick (2007) provide this additional background:
Bar modeling is a specific variant of the common Draw a Picture mathematics problem solving strategy. Because Singapore Math® uses this one variant consistently, students know what kind of picture to draw. That’s an advantage if the bar model is versatile enough to apply to many complex problems—and it is. It is especially useful for problems that involve comparisons, part-whole calculations, ratios, proportions, and rates of change. It communicates graphically and instantly the information that the learner already knows, and it shows the student how to use that information to solve the problem. (p. 28)
When learning with a model approach, students create diagrams to represent problems and concepts with bars. Drawing these types of models helps students to visualize strategies for problem solving and to make algebraic concepts more concrete. Model drawing can
- help students solve simple and complex word problems;
- develop algebraic thinking;
- help students visualize the part-whole structure of
the problem; - develop students’ operational sense; and
- foster proportional reasoning.
How Math in Focus Delivers
Bar models are used to aid visualization, understanding, and the extraction of information within a math expression or word problem, helping students to grasp the “why” and “how” of problem solving and consolidate the conceptual and computational skills required for mastery. The bar model method is first introduced in Grade 2 and then used through middle school’s Course 2.

According to the Curriculum Planning and Development Division (CPDD) of Singapore’s Ministry of Education (2012), metacognition, or “thinking about thinking,” refers to the awareness of, and the ability to control one’s thinking processes, in particular the selection and use of problem-solving strategies. It includes monitoring one’s own thinking and level of understanding, as well as self-regulating learning (NRC, 2001). “(C)ognitive science studies of problem solving have documented the importance of adaptive expertise and of what is called metacognition: knowledge about one’s own thinking and ability to monitor one’s own understanding and problem solving activity” (NRC, 2001, p. 118).
Researchers have found that Asian countries, particularly those in the Pacific Rim, have for decades based their education systems and practices upon the idea that learning is a process determined by effort, rather than fixed notions of ability—and such attitudes can be attributed to more successful instructional outcomes in this part of the world (Boaler, 2013; Sahlberg, 2011; Stigler & Hiebert, 1999).
The National Council of Teachers of Mathematics (2014) urges educators to elicit and use evidence of student thinking to evaluate progress toward mathematical understanding and to adjust instruction continually in ways that support and extend learning.
A concept pioneered by psychologist Carol Dweck (2006; 2008), growth mindset is a belief that a person’s intelligence, competence, and talents can be developed through dedicated efforts and hard work. “To ensure that all students have access to an equitable mathematics program, educators need to identify, acknowledge, and discuss the mindsets and beliefs that they have about students’ abilities” (NCTM, 2014, p. 64).
The National Research Council’s How People Learn: Brain, Mind, Experience, and School (Bransford, et al., 2000) cited the importance of educators fostering metacognition to allow students to take control of their own learning and monitor their own progress: “Teaching practices congruent with a metacognitive approach to learning include those that focus on sense-making, self-assessment, and reflection on what worked and what needs improving. These practices have been shown to increase the degree to which students transfer their learning to new settings and events” (p. 12).
Studies have determined that there is a significant correlation between metacognition and academic achievement and that training in the use of metacognitive skills increases achievement; researchers have also discovered relationships between metacognition and study habits and attitudes (Ozsoy, Memis, & Temur, 2009).
Within how children learn mathematics specifically,“[m]etacognition and adaptive reasoning both describe the phenomenon of ongoing sense making, reflection, and explanation to oneself and others” (Donovan & Bransford, 2005, p. 218).
Students’ metacognition helps them to apply mathematical learning to new contexts: “By describing their own processes, students can use their reflections to develop flexible prototypes of experiences that can be drawn on in future problem solving” (Lesh & Zawojewski, 2007, p. 770).
A growth mindset within mathematics emphasizes teaching and learning as processes that cultivate mathematical abilities; stresses that success in school is a reflection of effort, not aptitude; and discourages messaging that some people are simply “bad at math,” instead promoting the belief that all students are capable of participating and achieving in mathematics. Within the United States, mindsets have contributed to persistent negative perceptions within mathematics as society has traditionally rewarded math students who memorize well and calculate fast, rather than others who possess equal potential but may be deeper, slower, and possibly more creative in understanding (Boaler, 2011, 2016; Dweck, 2008; NCTM, 2014).
Promoting and supporting growth mindsets can make an enormous positive impact on mathematics achievement: setting and supporting rigorous expectations and a genuine belief that student effort and effective instruction outweigh “smarts” and circumstances increase students’ opportunities to learn and motivates them to persevere through challenging tasks (Boaler, 2011, 2016; Dweck 2006, 2008; NCTM, 2014).
Productive perseverance is essential to the process of learning mathematics with understanding. (Hiebert & Grouws, 2007; NCTM, 2014; Warshauwer, 2015). When carefully supported toward a resolution and given appropriate time to figure something out that is not immediately apparent, students can engage in efforts that advance their thinking and deepen their understanding, while also gaining additional practice. This complex process of perseverance with mathematical problems and ideas develops metacognition, curiosity, stamina, and confidence (Goldenberg et al., 2015; Hiebert & Grouws, 2007). Given opportunity to make mistakes and persist through their challenging content, students have shown greater understanding on posttest measures than their counterparts (Kapur, 2010). Math teachers must create a classroom culture that demonstrates how challenge is a natural part of the learning process (Star, 2005).
Additionally, problem solving encourages students to see that their actions can lead to intellectual growth, and this “focus on the potential of students to develop their intellectual capacity provides a host of motivational benefits” (Black, Trzesniewski, & Dweck, 2007, p. 260). “As students build strategic competence in solving nonroutine problems, their attitudes and beliefs about themselves as mathematics learners become more positive. The more mathematical concepts they understand, the more sensible mathematics becomes. . . . Similarly, when students see themselves as capable of learning mathematics and using it to solve problems, they become able to develop further their procedural fluency or their adaptive reasoning abilities” (NRC, 2001, p 131). Writing during math instruction has also been found to give students more confidence in their math abilities, create more positive attitudes toward math, and help students understand complex math concepts (Furner & Duffy, 2002; Taylor & McDonald, 2007).
In mathematics, proficiency is linked to motivation and mindset. “In addition to the concepts and skills that underlie mathematical proficiency, children who are successful in mathematics have a set of attitudes and beliefs that support their learning. They see mathematics as a meaningful, interesting, and worthwhile activity; believe that they are capable of learning it; and are motivated to put in the effort required to learn” (NRC, 2001, p. 171). For this reason, teaching students the strategies to be proficient in mathematics is essential. “Because it leads to better performance, strategy use raises self-efficacy and motivation. Use of strategies relates positively to achievement and self-efficacy” (Schunk, Pintrich, & Meece, 2008, p. 310).
Gaining a strong conceptual foundation in mathematics develops students’ positive attitudes about the subject area and their confidence in their academic futures more broadly. Indeed, according to the National Research Council (2001): “Students’ disposition toward mathematics is a major factor in determining their educational success” (p. 131).
How Math in Focus Delivers
Metacognitive awareness can be effectively developed through:
- exposure to general problem solving skills, thinking skills, and heuristics, and how these skills can be applied to solve problems;
- modeling of strategies and methods for solving problems, as through think-alouds;
- problems that require planning (before solving) and evaluation (after solving);
- encouragement to seek alternative ways of solving problems;
- requiring students to check the appropriateness and reasonableness of answers; and
- allowing students to discuss how to solve a particular problem and to explain the different methods for solving the problem.
Math in Focus embeds communication and reflection opportunities throughout the program so that students are able to discuss their thinking and consider on the math they are practicing. The Math Journal is one of the ways that students are able to reflect on their own learning.
Metacognition is foundational to the Math in Focus program. The concrete to pictorial to abstract sequence provides the structure necessary for students to grasp the “how and why” of mathematical concepts. Discussion is encouraged through Hands-On activities and investigation and reasoning skills are enhanced through the Let’s Explore! and Put On Your Thinking Cap! activities.
Each new chapter in Math in Focus features activities to help students recall prior knowledge necessary for building new concepts and skills. Common Error alerts for identifying and correcting common misconceptions and Best Practice tips for effective instruction and classroom management are also provided so that the teacher can focus on giving support necessary for students to succeed with new content and gain confidence. The multi-models used to present the new concepts motivate students to complete the two-step and multistep problems they encounter in the Hands-On activity and the Let’s Explore! investigative activities.
Additionally, the Learning Continuum feature provides exemplar problems to demonstrate prerequisite skills taught, the concepts and skills students will learn in the upcoming chapter, and what they will learn next. Teachers can also revisit learning objectives of prior knowledge relevant to the chapter.
“[L]earning is said to have occurred when students develop an understanding of the relationships between and among concepts and between concepts and procedures” (Stein, Remillard, & Smith, 2007, p. 331). This statement is especially true within mathematics education, where conceptual understanding is one’s “integrated and functional grasp of mathematical ideas. Students with conceptual understanding know more than isolated facts and methods. They understand why a mathematical idea is important and the kinds of contexts in which it is useful. They have organized their knowledge into a coherent whole, which enables them to learn new ideas by connecting those ideas to what they already know” (NRC, 2001, p. 118).
“Representing is central to mathematics” (Cross, Woods, & Schweingruber, 2009, p. 42). It is a widely held understanding that mathematical models and representations help to make mathematical concepts more concrete (Bobis & Way, 2018; NCTM, 2000, 2014; Stylianou, 2011). “Because of the abstract nature of mathematics, people have access to mathematical ideas only through the representations of those ideas” (NRC, 2001, p. 94).
The National Council of Teachers of Mathematics (2000) recommends that K–12 instructional programs enable all students to
- create and use representations to organize, record, and communicate mathematical ideas;
- select, apply, and translate among mathematical representations to solve problems; and
- use representations to model and interpret physical, social, and mathematical phenomena.
“Representations should be treated as essential elements in supporting students’ understanding of mathematical concepts and relationships; in communicating mathematical approaches, arguments, and understandings to one’s self and to others; in recognizing connections among related mathematical concepts; and in applying mathematics to realistic problem situations through modeling” (NCTM, 2000, p. 67).
At every level, teachers and learners of mathematics use pictures or diagrams to represent situations. In mathematics, representations are not only written numbers or equations but also include images, simple drawings, graphs, and other ways to see and think about mathematical ideas. Math drawings are tools for modeling, sense making, reasoning, explaining, structuring, and generalizing. “[I]magery based processes play an important role in all levels of mathematical problem solving” (Campbell, Collis, & Watson, 1996, p. 177). When students sketch or organize their mathematical thinking, they are able to explore their understanding of concepts, procedures, and processes—and communicate mathematically (Stylianou & Silver, 2004).
Visualization is important within and to the concrete–pictorial–abstract approach as students learn and understand mathematical concepts as a progression from objects to pictures to symbols (Leong, Ho, & Cheng, 2015; Salingay & Tan, 2018; Agrawal & Morin, 2016; Jordan, Miller & Mercer, 1998). Visualization and representation may also foster mathematical intuition, which according to Jerome Bruner, a leading cognitive theorist and educational psychologist of the 20th century, is “the class of non-rigorous ways by which mathematicians speed toward solutions” (1979, p. 99), which precedes analytical language of mathematics or the translation of intuitive ideas into mathematics.
These representations enable teachers to explain and learners to understand situations quantitatively or geometrically. Representations bolster intuition and understanding (Blatto-Vallee, Kelly, Gaustad, Porter, & Fonzi, 2007) and can help students to communicate, reason, problem solve, connect, and learn (Hill, Sharma, Obyrne, & Airey, 2014). Representations “help to portray, clarify, or extend a mathematical idea by focusing on its essential features” (NCTM, 2000, p. 206). Researchers have concluded that visualization is a powerful problem-solving tool and can be helpful in all kinds of mathematical problems, not only geometric problems (Van Garderen, 2006).
Manipulatives are visual representations as well; the term is used to refer to those concrete materials— such as blocks, cubes, base-ten blocks, place value cards, fraction strips, and so on—that teachers employ to develop students’ mathematical understandings and skills. In addition to being manipulable and grounded in the concrete world, manipulatives also provide teachers and students with a visual point from which to have conversations about mathematical topics, concepts, and situations (Thompson & Lambdin, 1994). Research suggests that manipulatives can be effective in increasing students’ mathematical knowledge (Clements & McMillen, 1996; Clements & Sarama, 2007b), particularly when care is taken in how students interact with the manipulatives. While manipulatives can be a primary vehicle for constructing knowledge, students will not automatically draw the same conclusions that their teachers draw; they must be helped to see the connections among the object, symbol, language, and concept (Ball, 1992a, 1992b).
Young students and students having difficulty grasping abstract mathematical concepts benefit from visual representations of mathematical ideas, including physical objects or actions they perform as they are trying to solve problems (NRC, 2001). Including visuals in the classroom can be particularly supportive of English learners and at-risk students (Fuson, Atler, Roedel, & Zaccariello, 2009; Fuson, Smith, & Lo Cicero, 1997). The efficacy of representative approaches to mathematics instruction extends beyond the elementary level with which it is typically associated. Using visual representations has been shown to improve student performance in general mathematics, pre-algebra, word problems, and operations (Gersten et al., 2009).
“For students to understand such mathematical formalisms, we must help them connect these formalisms with other forms of knowledge, including everyday experience, concrete examples, and visual representations. Such connections form a conceptual framework that holds mathematical knowledge together and facilitates its retrieval and application” (Donovan & Bransford, 2005, p. 364).
Visualization and representation are central to mathematics in Singapore Math®. “[T]he Singapore [math approach] illustrations demonstrate how to graphically decompose, represent, and solve complicated multi-step problems” (Ginsburg et al., 2005, p. XII). “It was found that the Singapore textbook included features that can help pupils acquire strong foundations in mathematics as well as develop good habits of mind. . . . The strong foundation is achieved through extensive use of pictorial representations, especially in the early part of the development of a skill or concept” (Har, 2005, online).
How Math in Focus Delivers
- Visual representation is a hallmark of Math in Focus. Powerful models are featured throughout program levels to build and extend conceptual understanding.
- The use of ten frames builds understanding of counting, adding, and subtracting numbers in relation to the key value of 10.
- The use of number bonds builds understanding of number relationships and supports a flexible, robust knowledge of number facts.
- The use of number lines builds understanding of whole numbers, fractions, and decimals, both in the relationships between representations and in how quantities compare to each other.
- The use of place value charts builds understanding of the meaning of digits in base-ten number representations and how these representations are used in the four operations, supporting a conceptual grasp of standard algorithms.
- The use of fraction models builds understanding of fractions as parts of a whole, how to compare these parts, and how they interact under addition, subtraction, multiplication, and division.
- Math in Focus also includes manipulative kits and virtual manipulatives.
The use of problem variations within concept formation can help students discern what the essential features of mathematical concepts are—and what they are not. Variation can also provide effective scaffolding for problem solving (Cai & Nie, 2007). In this process, ‘‘students’ experience in solving problems is manifested by the richness of varying problems and the variety of transferring strategies’’ (Gu, Huang, & Marton, 2004, p. 322).
The theory behind variation pedagogy is based on the presumptions that because “learning is about developing new ways of seeing or experiencing the object of learning, it is necessary to experience certain patterns of variation and invariance in order to discern critical features of the object of learning. Teaching then means to construct appropriate spaces of variation” (Huang & Li, 2017, p. 3).
Teaching and learning through variation has been practiced in China for centuries, and the exam-driven education system as well as traditional cultural values and ancient mathematical ideas within China have reinforced its wide use (Gu, Huang, & Gu, 2017). In the mid-20th century, Zoltan Dienes advanced the pedagogy through his work designing approaches to aid children’s understanding of higher-order mathematical concepts and prescribing that teachers provide multiple representations of a concept, rather than repeating the same experience multiple times. Dienes postulated two theories: the perceptual variability principle that claims conceptual learning is maximized when children are exposed to a concept through a variety of physical contexts or embodiments using a variety of materials to promote abstraction; and the mathematical variability principle, which suggest that children must experience numerous variations of complicating factors linked to the structure of a concept in order to single out the general mathematical concept constant to all manipulations. Dienes viewed these principles as complementary and the application of both essential to the process of learning a math concept involving both abstraction and generalization (Dienes, 1971, 1973; Gningue, 2006).
Variation in mathematics pedagogy has been examined empirically in recent decades. Results show much promise for expanding variation more broadly via appropriate implementation (Gu et al., 2017). Teaching through variation tasks has been demonstrated as an effective way to promote meaningful, active math learning within large-size classes (Gu et al., 2004).
In teaching with variation, a series of related problems are presented to help students understand a concept, master a problem-solving method, or make a generalization. When learning mathematical concepts, students are provided a series of problems in which essential features of mathematical concepts are kept unchanged, but the nonessential features of mathematical concepts are changed (Cai & Nie, 2007).
According to Gu et al. (2017), there are two main forms of variation in mathematics instruction. Conceptual variation consists of designing variation problems based on essential features of a concept and comparing and contrasting concept and nonconcept images to help students clarify connotations and extensions of a concept; when this process includes, as a geometric example, reconfiguring the structure of a complex figure and forming a figure through transformation of basic figures, cognitive load is reduced and deeper understanding is promoted. The other form, procedural variation, refers to creating variation problems or situations for students to explore in order to find solutions to problems or develop connections among different concepts step by step or from multiple approaches.
How Math in Focus Delivers
Drawing on research indicating that understanding deepens when students are made to look at mathematical concepts from different perspectives and within new contexts or situations, Math in Focus utilizes variation principles to help students encounter a concept in its multiple facets to support mastery. The program presents concepts with such variation to challenge students to adapt their mathematical skills flexibly.
Routine problems entail the application of a specific computation, while nonroutine problems are complex, lack immediately apparent solutions, and require some degree of creativity or originality to solve. Nonroutine problems typically demand the use of strategies, or heuristics, and often have multiple solutions. Polya (1971) described problems that don’t lend themselves to mechanical application of straightforward algorithms, now called nonroutine problems, as the problems in which you have to figure out how to proceed, as well as to calculate successfully.
It is important to affirm the value of problem-based learning by requiring students to work through extensive problem sets that include routine and nonroutine applications in a wide variety of real-world contexts (NRC, 2001). It is also important that problem-solving activities foster flexibility. “Flexibility develops through the broadening of knowledge required for solving nonroutine problems rather than just routine problems. . . . (N)onroutine problems are problems for which the learner does not immediately know a usable solution method. Nonroutine problems require productive thinking because the learner needs to invent a way to understand and solve the problem” (NRC, 2001, p. 126).
Research has demonstrated that struggling to make sense of mathematics is a necessary process in learning mathematics with understanding (Hiebert & Grouws, 2007; Warshauwer, 2015). Teachers who guide students through such productive perseverance are supporting the development of student learning and understanding. When carefully supported toward a resolution and given appropriate time to make sense of mathematics, to figure something out that is not immediately apparent, students can engage in efforts that advance their thinking and play an important role in deepening their understanding. Such a process provides students with the opportunity to practice and engage (Goldenberg et. al., 2015).
Singapore mathematics curriculum and textbooks teach specific strategies for problem solving via what Polya (1971) called heuristics. As part of effective mathematics instruction, teachers should present nonroutine and open-ended problems in such ways that will develop students in the use of thinking skills and heuristics (Ho, Teong, & Hedberg, 2004).
“The development of strategies for solving nonroutine problems depends on understanding the quantities involved in the problems and their relationships as well as on fluency in solving routine problems. Similarly, developing competence in solving nonroutine problems provides a context and motivation for learning to solve routine problems and for understanding concepts such as given, unknown, condition, and solution” (NRC, 2001, p. 127).
How Math in Focus Delivers
Math in Focus is based on the belief that applying concepts and skills builds real-world problem solvers and, to accomplish this, the program embeds problem solving throughout each section.
Word problems grow in complexity from one-step to two-step to multistep, which enhances the students’ ability to think critically in a systematic process. Students learn to use model drawing strategies to represent problems, which provides students with the skills and strategies necessary to approach both routine and nonroutine problems.
Challenging, nonroutine questions are presented in the Put On Your Thinking Cap! problems. To solve these problems, students must draw on both prior knowledge and recently acquired skills and concepts as well as think critically about how to best combine problem-solving strategies.
Conceptual understanding in mathematics provides students with an integrated and functional grasp of mathematical ideas that transcends beyond knowing isolated facts and methods; rather, students with conceptual understanding recognize why a mathematical idea is important and purposefully access and apply knowledge into appropriate and useful contexts (Cross et al.,, 2009; NRC, 2001).
“Learning the ‘basics’ is important; however, students who memorize facts or procedures without understanding often are not sure when or how to use what they know. In contrast, conceptual understanding enables students to deal with novel problems and settings. They can solve problems that they have not encountered before” (NCTM, 2000, online).
The National Council of Teachers of Mathematics (2014) stresses that conceptual understanding underpins mathematical learning: “Effective teaching of mathematics builds fluency with procedures on a foundation of conceptual understanding so that students, over time, become skillful in using procedures flexibly as they solve contextual and mathematical problems” (p. 42).
Research findings indicate effective instructional approaches to foster conceptual understanding in mathematics. As NCTM (2014) stresses, it is essential that conceptual understanding and procedural fluency be developed in tandem. In a review of research, Hiebert and Grouws (2007) determined that “instruction emphasizing conceptual development facilitated skill learning as well as conceptual understanding” (p. 387).
In their study of mathematics learning in early childhood, Cross and colleagues (2009) concluded that to effectively foster students’ conceptual understanding, teachers must include four key elements or opportunities within their teaching and learning activities: analyzing and reasoning; creating; integrating; and making real-world connections. Discussions of cognitively challenging mathematical topics and ideas are also a primary mechanism for promoting conceptual understanding (Michaels, O’Connor, & Resnick, 2008).
Problem-based instruction facilitates conceptual development. “Developing mathematical understanding requires that students have the opportunity to present problem solutions, make conjectures, talk about a variety of mathematical representations, explain their solution processes, prove why solutions work, and make explicit generalizations” (Franke et al., 2007, p. 230).
Metacognitive awareness is essential to concept development. Booth, Lange, Koedinger, and Newton (2013) found that explaining worked examples—both correct and incorrect—during practice fostered deeper conceptual understanding. Also, students must have opportunities to apply what they learn. “Knowledge that is taught in only a single context is less likely to support flexible transfer than knowledge that is taught in multiple contexts. With multiple contexts, students are more likely to abstract the relevant features of concepts and develop a more flexible representation of knowledge” (Bransford et al., 2000, p. 78).
How Math in Focus Delivers
Math in Focus provides opportunities in each chapter for students to develop deeper understanding through exploration, discussion, and reflection. Participation in the Hands-On activities, Games, Let’s Explore!, Math Sharing, Put On Your Thinking Cap!, and Math Journal all encourage concept and skill development as well as present extensive practice with problem solving and reasoning.
Multipage and multiday sections provide the support and time needed to allow students to gain a deep understanding of concepts through multiple approaches. Each chapter in Math in Focus uses multiple approaches to introduce and build on new concepts. For example, in kindergarten students may use cubes to count and compare in the Learn activity, and then use cutouts in the Hands-On activity to further develop the count and compare concept.
The National Research Council (2001) identifies procedural fluency as one of the five strands of mathematical proficiency and defines it as skill in carrying out procedures flexibly, accurately, efficiently, and appropriately. The National Council of Teachers of Mathematics (2014) emphasizes the importance of procedural fluency within mathematics learning as well as its recursive connection with conceptual understanding, urging that, for students to achieve understanding, instruction must recognize and support the relationship. Effective mathematics instruction cannot have one without the other as “procedural knowledge and conceptual understandings must be closely linked” (NRC, 2005, p. 232).
According to NCTM (2014), students need procedures that they can use with understanding on a wide range of problems. The concrete–pictorial–abstract approach is effective for learning mathematical concepts as a progression from objects to pictures to symbols (Leong et al., 2015; Salingay & Tan, 2018; Agrawal & Morin, 2016; Jordan et al., 1998). CPA in tandem with manipulatives provides further boost to the teaching of important mathematical concepts (Miller & Hudson, 2007).
Additionally, “like all language skills, learning the language of mathematics is an important goal for all students and can remove barriers to learning mathematical ideas” (Dacey, Lynch, & Salemi, 2013, p. 149). A wide body of research supports the important role of communication in the mathematics classroom. Two National Research Council reports—Adding It Up (2001) and How Students Learn: Mathematics in the Classroom (2005)—emphasize discussion as a way to increase students’ mathematical understanding. Per NCTM (2000), “Communication is an essential part of mathematics and mathematics education. . . . Communication can support students’ learning of new mathematical concepts as they act out a situation, draw, use objects, give verbal accounts and explanations, use diagrams, write, and use mathematical symbols” (pp. 59–60).
A long-established body of research has affirmed the importance of communication in the mathematics classroom. For example, Lovitt and Curtiss (1968) found that encouraging a student to verbalize problems before giving a written response increased the rate of correct answers. Communicating about math improves learning; “encouraging students to verbalize their current understandings and providing feedback to the student increases learning” (Gersten & Chard, 2001, online).
When students write about and discuss math concepts, they have the chance to think through, defend, and support their ideas. A review of studies found that the process of encouraging students to verbalize their thinking—by talking, writing, or drawing the steps used in solving a problem—is consistently effective (Gersten et al., 2007).
Supporting English learners (ELs) in developing the language of math is especially important. Janzen’s 2008 review of research on teaching English learners in mathematics shares that while many perceive that math is easier for ELs to learn because it involves numbers, mathematics actually presents specific language challenges to this student population. Similarly, working in a transitional language classroom led researchers Bray, Dixon, and Martinez (2006) to conclude that as students “communicate verbally and in writing about their mathematical ideas, they not only reflect on and clarify those ideas but also begin to become a community of learners” (p. 138). When introducing academic words to English learners’ expressive vocabularies, students respond best to classrooms that are routine and offer frequent and comfortable opportunities to express what they have learned (Feldman & Kinsella, 2008).
When students use language in ways that are purposeful and meaningful for themselves, in their efforts to understand—and be understood by—each other, they are motivated to attend to ways in which language can be both clarified and clarifying (Mondada & Doehler, 2004).
How Math in Focus Delivers
Math in Focus provides continuous opportunities for students to communicate and reflect on the mathematics they are practicing. By working in pairs or small groups through the Hands-On activities or Let’s Explore!, students are able to discuss their thinking and their reasoning and therefore further develop their understanding of the concepts being presented. The Math Journal provides students with a chance to write and reflect on their mathematical learning, while Math Talk and Math Sharing generate discussion and foster deeper understanding.
Language Development gives tips and suggestions for reinforcing vocabulary for English learners.
“An excellent mathematics program requires effective teaching that engages students in meaningful learning through individual and collaborative experiences that promote their ability to make sense of mathematical ideas and reason mathematically” (NCTM, 2014, pp. 4). Math in Focus utilizes research-based best practices and approaches to instruction in order to deliver highly effective mathematics instruction.
The sustained use of an effective, research-based instructional model, particularly when implemented consistently, has been shown to help students learn fundamental concepts (NRC, 2000 & 2005; Bybee et al., 2006).
The use of learning cycles in the classroom supports a constructivist approach and aids in connecting learning to real-life situations (Blank, 2000; Lawson, 2001). Importantly, the learning cycle approach also encourages students to examine the adequacy of the prior conceptions they bring with them to the classroom, and then requires students to test and argue about those beliefs; when predictions based on those prior beliefs are contradicted, students also have an opportunity to construct more adequate concepts and gain skills in reasoning patterns (Lawson, 2001).
Numerous studies conducted over five decades have proven that the learning cycles approach yields increased understanding of concepts and generalizable reasoning skills in students across the elementary to post-secondary levels (Bybee et al., 2006; Lawson, 2001). Further, when a metacognitive component is added to the learning cycle, providing opportunities for students and teachers to talk through the thinking, idea formation, and status of their conceptions, students showed a greater permanent restructuring of their understandings of content (Blank, 2000).
The National Council of Teachers of Mathematics (2000) supports instruction that takes a developmental perspective: starting and building on what children know and leading them to construct relational understanding, problem-solving abilities, and the ability to reason logically. “Understanding grows as webs of interrelated ideas become more complex, and this happens in classrooms that contain rich experience, time for integration and reflective thought, and opportunities to take action and use what is known” (Zambo & Zambo, 2007, p. 266).
The learning cycle essentially consists of sensing, integrating, and acting. During a mathematics learning cycle, students’ brains take in sensory experiences, integrate new content with what they already know, reflect on information, and formulate plans to enact ideas. In the process and influenced by the quantity and quality of classroom experiences, students’ brains are building structures and forging neural connections that they will use to understand mathematical concepts and procedures. The learning cycle occurs specifically within the cerebral cortex, the part of the brain largely responsible for the thinking and learning that happens when children are engaged in problem solving and higher-level mathematics (Berninger & Richards, 2002; Zambo & Zambo, 2007).
How Math in Focus Delivers
Part I: Engage
The focus cycle starts with an Engage task that connects to prior learning and provides an inquiry-based opportunity for students to enter a task cycle. For example, consider the following Engage task: Use fraction pieces to show your thinking. Audrey had one-third of a pie. She shared her portion equally with her brother. How much pie did they each receive? Explain your method.
By providing students with the opportunity to first build and then explain their reasoning, the Engage task connects student learning to prior experiences with dividing fractions. It helps students construct meaning through the use of physical or visual models, which ultimately lead to abstract representations.
Part II: Learn
The second part of the focus cycle emphasizes exploration of the variation of a mathematical concept. In the Learn phase, students encounter both mathematical and perceptual variations of the task. One way mathematical variation occurs is by controlling the number strings that students will encounter.
Consider the number string:
210 x 4
132 x 3
204 x 2
225 x 3
What aspect is changing each time? By consciously controlling the mathematical variation of the task, we can predict where students might have difficulty and thus help them to form generalizations.
Perceptual variation occurs in the Learn cycle when students are introduced to multiple representations of a concept or problem. Consider 2-digit by 1-digit multiplication.
Part III: Try
The third part of the focus cycle is the Try phase, in which students take one more step toward generalization by practicing skills they explored during the Engage task, and then varied during the Learn phase. In the Try phase, students have the opportunity to synthesize their learning through guided practice. Each item in the Try phase is carefully designed as a formative assessment to monitor a student’s progress toward mastery and serves as an opportunity to discover which students might need to revisit a concept or skill.
Problem solving can be challenging for all students, but particularly those experiencing difficulty with mathematics learning in general (Fuchs, Fuchs, & Prentice, 2004; Gersten et al., 2009). However, reducing cognitive load for even underperforming students by either minimizing complexity or providing too much help or any direct answers is not the solution (Boston & Wilhelm, 2015; Goldenberg, et al., 2015). Struggling to make sense of mathematics is vital to learning mathematics with understanding (Hiebert & Grouws, 2007; Kapur, 2010; Warshauwer, 2015). As the National Council of Teachers of Mathematics emphasizes in Principles to Actions: Ensuring Mathematical Success for All (2014), “Effective teaching of mathematics consistently provides students, individually and collectively, with opportunities and supports to engage in productive struggle as they grapple with mathematical ideas and relationships” (p. 3).
The kinds of questions teachers ask and the kind of support that teachers offer are critical, as these could either facilitate or undermine the productive efforts of students’ struggles and determine whether students view struggle as a positive endeavor or the source of impediment and frustration (Warshauwer, 2015). Timing of support also plays a vital role. When scaffolding is given to students before they have the opportunity to make sense of a challenging task independently, without teacher assistance, they are inhibited from developing productive perseverance (Boston & Wilhelm, 2015; Dixon, 2018).
Research indicates that an effective means of improving students’ performance in problem solving is a schema-based approach that provides explicit instruction emphasizing the underlying structures of problems and utilizing heuristics and visual representations (Fuchs et al., 2004; Gersten et al., 2009; Jitendra et al., 2013).
Effectively problematizing mathematics entails asking students to think for themselves and to explain their thinking while supported by their teacher, classmates, and math program; to struggle productively; and ultimately to apply their gained knowledge and strategies to new and more complex problems they encounter in the future (Hiebert et al., 1996). This process serves the additional purpose of cultivating in students the belief that their efforts to persevere through challenge are the source of their success in math—which in turn motivates students to persist in their learning (Boaler, 2011, 2016; Dweck 2006, 2008; NCTM, 2014).
How Math in Focus Delivers
Think Problems are an important feature of Math in Focus. Think Problems appear within the introduction to a section or topic and ask a question for which students don’t yet have an algorithm or “answer”—but they have the building blocks to possibly figure it out. Through the section that follows, students will build the knowledge to be able to answer the question confidently by the end of the section. The Think Problem is then revisited at the end of the section (and sometimes each day). By the end, students are ready to answer it from a place of mastery.
In addition to providing productive struggle and discussion, Think Problems also motivate learning and help students build schemas. Think Problems stretch students’ mathematical thinking—and their ability to think mathematically.
Darling-Hammond (2010) studied the characteristics of assessment systems in high-performing nations and found that “they emphasize deep knowledge of core concepts within and across the disciplines, problem solving, collaboration, analysis, synthesis, and critical thinking. As a large and increasing part of their examination systems, high-achieving nations use open-ended performance tasks . . . to give students opportunities to develop and demonstrate higher order thinking skills” (p. 3).
Performance tasks that allow for a criterion-referenced evaluation of how students demonstrate knowledge and skill via writing, products, or behavior are essential to a well-rounded assessment plan in the mathematics classroom. Such assessments are also essential mechanisms for learning. Performance tasks allow students to make connections among important content knowledge and process skills emphasized in instruction and offer the opportunity for students to show how well they can use what they know to classify, compare, analyze, or evaluate as well as create a response or product teachers can use within a comprehensive approach to assessment (Hibbard, 1996).
Learning is an active process of engagement. If students are interested in what they are learning, they will persist in spending the time and energy needed for learning to occur (Guthrie & Humenick, 2004; Hidi & Boscolo, 2006). Helping students actively engage in authentic investigative practices, particularly in collaborative formats that entail seeking evidence and reasons for the ideas or knowledge behind claims, allows students to develop deeper understandings of content (Krajcik & Blumenfeld, 2006).
Learning is optimized when students make connections among ideas, both within mathematics and outside of the mathematics content. Making connections between new information and students’ existing knowledge—knowledge of other content areas and of the real world—has proved to be more effective than learning facts in isolation (Beane, 1997; Bransford, Brown, & Cocking, 2000; Caine & Caine, 1994. Further, connecting mathematics to science, social studies, and business topics can increase students’ understanding of and ability with mathematics (Russo et al., 2011).
Instructional methods that entail the utilization of information through problem-focused learning and the integration and application of knowledge in real-world settings fosters 21st-century skills and competencies (Merritt, Lee, Rillero, & Kanich, 2017; Capraro & Slough, 2013; Bell, 2010). A project-based approach toward teaching has been shown to be particularly effective in the areas of science, technology, and engineering, particularly with students who struggle in those areas (Han, Capraro, & Capraro, 2014).
Over the past decade or so, there has been concern reflected in policy, research, and practice about the declining state of STEM (science, technology, engineering, and mathematics) education in the United States. One promising remedy is an increased focus on these disciplines in a variant form known as STEAM—science, technology, engineering, arts, and mathematics (Taljaard, 2016). As a nascent and evolving pedagogy, STEAM is still being defined and explored as its being implemented; one influential view is that STEAM is “science and technology interpreted through engineering and the arts, all based in mathematical elements” (Yakman, 2008, p. 3)
Land (2013) outlines a rationale for this innovative, integrative push for STEAM in schools:
There is growing interest amongst forward looking public officials, educators, and professionals in enhancing the education platform to better prepare students for both analytical and creative thinking. Traditional STEM . . . degrees focus on convergent skills whereas art degrees focus on divergent skills. Having the ability to execute both at scale can better position our nation for global competitiveness. . . . With a STEM job market increasing three times faster than the rest of the economy, and only 4.4% of American undergraduates enrolled in STEM programs, there is a huge shortage of qualified high-tech workers. Education must foster not only problem solving skills but also problem seeking skills all while maintaining the interest of the students. (abstract)
“STEAM is a substantiated, economical and sociologically adaptable as a framework by which to transition, maintain, create and evolve educational elements, programs and institutions to include multidisciplinary-oriented practices catering to developing more functional citizens” (Yakman & Lee, 2012, p. 1077).
STEAM approaches to instruction allow for the integration of abstract mathematical ideas to find concrete solutions and evidence via art. Further, a problem-based approach can be an effective basis for integrating math learning into an interdisciplinary STEAM framework (Thuneberg, Salmi, & Fenyvesi, 2017). STEAM is best practiced in ways that foster real-world connections and require students to consider “big ideas” and apply learning to new contexts in order to find solutions (Watson & Watson, 2013; Land, 2013).
Thuneberg, Salmi, and Bogner (2018) surveyed research and report that current STEAM initiatives may provide new opportunities to learn abstract mathematical problem-solving tasks:
- Interactive, hands-on approaches in workshop-like settings can encourage students to use their senses to find creative solutions based on observation and experimentation.
- Aesthetic elements of art and handicrafts expose students to concrete space and shape experiences and promote understanding of mathematical concepts.
STEAM also has the potential the yield social-emotional benefits. Combining math and art encourages students to approach math problems from a new perspective, sparking imagination; when creative and imaginative products emerge from interdisciplinary projects and are shared with others, the process likely generates an emotional experience, which can further serve to support cognition and the retention of learned content and skills (Thuneburg et al., 2017). Yakman & Lee (2012) offer additional potential effects of STEAM:
Both the reasoning of why there is a global movement towards developing more people in the S-T-E-M fields, and the knowledge that there is something about these “hard” fields that make many choose paths of liberal arts studies, especially women and minorities, makes the concept of STEAM not only more than a possibility. It is critical for global culture that students be interested in these fields as well as be able to succeed in learning and developing themselves with professional and realistic attitudes and skills. (p. 1083)
How Math in Focus Delivers
To ground learning in real-world problems, Math in Focus has students engage in STEAM Project Work. This collaborative task promotes critical and creative thinking in science, technology, engineering, arts, and mathematics and provides real-world context for problem solving.
Math in Focus Performance Tasks are formative assessments that will show how well students have learned the concepts and skills. The rubric provides feedback for students on how to improve their problem-solving skills. Teachers are given guidelines for the formative assessment with an accompanying rubric.
Learning and doing mathematics requires many interrelated skills and knowledge; however, mathematics is not simply a body of content or procedures to be learned. Mathematics also encompasses ways of thinking in order to engage in practices and take a problem-solving approach, making connections and using productive reasoning. Students of math must demonstrate persistence when initial methods or strategies do not generate solutions. Students who are successful in mathematics are both creative and flexible in strategy use and conscientious, critiquing their solutions to ensure that they have found a reasonable solution to the problem. All of these approaches can be taught and developed through modeling, practice, and problem-solving opportunities—and they require mathematical habits of mind.
In their seminal article Cuoco, Goldenberg, and Mark (1996) proposed that “more important than specific mathematical results are the habits of mind used by the people who create those results . . . this includes learning to recognize when problems or statements that purpose to be mathematical are, in truth, still quite ill-posed or fuzzy; becoming comfortable with and skilled at bringing mathematical meaning to problems and statements through definition, systematization, abstraction, or logical connection making; and seeking and developing new ways of describing situations” (p. 376).
Mathematical habits of mind reflect how mathematicians think about situations in automated, internalized ways that allow them to persist through complex problems. Such problem-solving proficiency requires mastery not just of facts and procedures—the results of mathematical thinking—but also the practices of such thought processes and their accompanying behaviors. Additionally, the need for mathematical thinking extends well beyond the mathematics classroom. Developing mathematical habits of mind is essential to mathematical proficiency, critical thought, college and career readiness, access to future opportunities, and productive participation in society (Goldenberg et al., 2015).
Boaler works with Dweck on researching mathematical mindsets and delivering growth mindset interventions to teachers and students. A Stanford profile (Parker, 2015) cites Boaler’s work with the Program for International Student Assessment (PISA) tests team, analyzing their data set of 13 million students worldwide. A key finding was that the lowest achieving students are those who use a memorization strategy—while the highest performers are those who see math as a set of connected, big ideas. Per Boaler, “[w]hen we open up mathematics and teach broad, visual, creative math, then we teach math as a learning subject instead of as a performance subject” (Parker, 2015, online).
“If we really want to empower our students for life after school, we need to prepare them to be able to use, understand, control, modify, and make decisions about a class of technology that does not yet exist. That means we have to help them develop genuinely mathematical ways of thinking” (Cross et al., 2009, p. 21).
Researchers have advocated for using mathematical habits of mind as a framework for approaching math instruction for several decades, but the idea is timeless. Mathematics has always been about more than its products—facts, methods, formulas, etc.—as successful study within the field draws on cognitive practices such as strategies and behavioral dispositions such as perseverance to solve complex problems (Cuoco et al., 1996; Goldenberg et al., 2015).
Goldenberg and colleagues (2015) provide additional insight as well as lay out the stakes involved with mathematical habits of mind:
Competing in such a [complicated] world requires great adaptability to unexpected challenges. For that, workers need not only the skills for solving problems that we already know about but also the stamina and disposition to puzzle through totally unfamiliar problems for which we cannot now provide methods and procedures. The ability to solve new and unforeseen problems requires mastery not just of the results of mathematical thinking (the familiar facts and procedures) but of the ways that mathematically proficient individuals do that thinking. This is especially true as our economy increasingly depends on fields that require mathematics. Mathematical proficiency depends also on other mental habits that dispose one to characterize problems (and solutions) in precise ways, to subdivide and explore problems by posing new and related problems, and to “play” (either concretely or with thought experiments) to gain experience and insights from which some regularity or structure might be derived. (p. 1–2)
Questions are integral to developing mathematical habits. “Effective teaching of mathematics uses purposeful questions to assess and advance student reasoning and sense making about important mathematical ideas and relationships” (NCTM, 2014). While types of questions vary from asking students to recall facts to requesting an explanation for an answer, presenting questions throughout the learning process is necessary to understanding how students are making sense of the math.
Teachers’ questions are crucial in helping students make connections and learn important mathematics concepts. Questions are a means of both fostering understandings and evaluating understandings (Weiss & Pasley, 2004).
McTighe and Wiggins, authors of Essential Questions: Opening Doors to Student Understanding (2013), provide guidance on what makes a question essential. Essential questions are important for stimulating student thinking and inquiry as well as for helping teachers target standards and other goals for learning outcomes. Essential questions should develop and deepen students’ understanding of important ideas and processes so that students can transfer their learning within and outside school. McTighe and Wiggins recommend that content be unpacked to identify long-term transfer goals and desired understandings in a process that entails the development of associated essential questions. In other words, essential questions can be used to effectively frame key learning goals. Targeted understandings and essential questions are intrinsically related. In addition to addressing goals for learning, essential questions can be characterized as provocative and generative. They are open-ended; thought provoking; require higher-order thinking; spark additional questions; point toward larger, transferable ideas; require justification; and recur across the curriculum.
The following are overall essential questions for mathematics provided by McTighe and Wiggins (2013, p. 64):
- How is mathematics used to quantify and compare situations, events and phenomena?
- What are the mathematical attributes of objects or processes and how are they measured or calculated?
- How are spatial relationships, including shape and dimension, used to draw, construct, model and represent real situations or solve problems?
- How is mathematics used to measure, model and calculate change?
- What are the patterns in the information we collect and how are they useful?
- How can mathematics be used to provide models that help us interpret data and make predictions?
- In what ways can data be expressed so that its accurate meaning is concisely presented to a specific audience?
- How do the graphs of mathematical models and data help us better understand the world in which we live?
- What do effective problem solvers do, and what do they do when they get stuck?
“All young Americans must learn to think mathematically, and. . . think mathematically to learn”(National Research Council, 2001, p. 1)
McTighe & Wiggins (2013, p. 76-77) also provide essential questions that support the CCSS Mathematical Practice Standards:
1. Make sense of problems and persevere in solving them.
What kind of a problem is this? What must be found? What is known? What is unknown? What counts as an adequate solution? Does my answer make sense? Does my approach make sense? What should I do if I’m stuck solving it? What similar problems does this remind me of? What simpler or special cases can help me?
2. Reason abstractly and quantitatively.
What’s the abstract relationship between these specific quantities? What does this quantitative relationship mean? How can I decontextualize the numbers to find a mathematical relationship? Have I represented the relationships between the quantities appropriately? Which operations and equivalences will simplify and help me solve the problem? Does my abstract representation of these quantities make sense in context?
3. Construct viable arguments and critique the reasoning of others.
Has this been proven? What is assumed? On what assumptions does that inference depend? Where might this assumption logically lead? Is the conclusion logical? Is the conclusion plausible? Have I sufficiently supported
my answer and shown my work? Which of these solutions is more plausible? Does this argument make sense? What might be counter-evidence and counter arguments to what I have concluded?
4. Model with mathematics.
What mathematics applies to this situation and this data? What simplifications or approximations, should I make in order to make a mathematical model of this phenomena/data/experience? How might the model be refined to be less simplistic and crude? Does this model make sense in this context? How might I test this model? What are the limits of this (or any) mathematical model? How might this model be improved?
5. Use appropriate tools strategically.
What tools should I use here to be most efficient and effective? What are the strengths and weaknesses of the tools at hand, and might there be better ones for the task? Where might I find more helpful resources when needed?
6. Attend to precision.
What is the appropriate degree of precision for this particular data and solution? Have I made my data, reasoning, and conclusion sufficiently clear (for this audience and purpose)? What terms need to be clearly defined? Have I tested the accuracy of my answer? How sure am I? How much statistical confidence should we have in the answer?
7. Look for and make use of structure.
What’s the underlying pattern here? What’s the whole, if that’s a part? What are the parts, if that’s the whole? What type of problem is this? What equivalences or re- constitutions of the problem are likely to help me see a pattern or structure? What shift of perspective might make the solution path more evident?
8. Look for and express regularity in repeated reasoning. What regularities suggest a constant relationship at work? What is a summary or shorthand way of expressing these recurring patterns? What patterns are evident? Am I sure that the general pattern recurs or is my sample too small? Is that a reasonable way to describe the perceived patterns?
How Math in Focus Delivers
Math in Focus instructional materials support teachers in developing the next generation of thinkers and learners with solid mathematical habits. The program engages students in inquiry and builds confidence and skills in problem solving via effective questioning and demonstrating how mathematics impacts their daily lives—and futures.
There are eight mathematical habits used throughout Math in Focus:
- Persevere in solving problems
- Construct viable arguments
- Use tools strategically
- Make use of structure
- Use mathematical reasoning
- Use mathematical models
- Use precise mathematical language
- Look for patterns
Effective instruction in mathematical problem solving is often situated within a meaningful or real-world context and encourages students to make connections. These connections—among mathematical ideas, with other content areas, and in real-world contexts—are an essential part of mathematical thinking and learning. Making connections between new information and students’ existing knowledge—knowledge of other content areas and of the real world—has proved to be more effective than learning facts in isolation (Beane, 1997; Bransford, Brown, & Cocking, 2000; Caine & Caine, 1994). Application can be motivational and interesting, and students at all levels need to connect the mathematics they are learning to the world around them (Alberti, 2013). Further, forging interdisciplinary connections between mathematics and science, social studies, art, business, and other areas can increase students’ understanding of and ability with mathematics (Russo et al., 2011).
Students see the purpose, relevance, and value of learning when they experience it in real-world contexts: “When instruction is anchored in the context of each learner’s world, students are more likely to take ownership for . . . their own learning” (McREL, 2010, p. 7). According to Fosnot and Dolk (2001), teaching with contextual problems can be effective for developing “children’s mathematical modeling of the real world” (p. 24). Students learn best when what they learn seems relevant. Personal connections to tasks improve students’ perception of the content as interesting and beneficial, thereby increasing their motivation to learn (Czerniak, Weber, Sandmann, & Ahem, 1999).
Blumenfeld, Kempler, and Krajcik (2006) explain how authenticity is an important element in effective instruction. Authenticity is achieved by drawing connections between the real world and knowledge or practice in the discipline via transformation of knowledge. There are various ways to forge real-world contexts for content to be learned. Drawing connections to students’ personal lives, emphasizing the value of a skill outside the classroom, and embedding new concepts and skills within meaningful tasks enhance value. Problem-based learning that situates important subject matter within driving questions or real-world issues or events can aid understanding and/or provide reasons or rationale for effort. Ideal contexts for learning provide students with multiple opportunities to work with concepts as well as clear purpose, plus yield from students a final product or artifact that motivates students with real-world value and a venue for cognitive engagement and knowledge transformation.
Learning cycles in the classroom support a constructivist approach and aid in connecting learning to real-life situations (Blank, 2000; Lawson, 2001). According to Ojose (2008), learning that connects with the real world aligns in particular with the developmental needs of students in Piaget’s formal operations stage during later elementary school. Children at this stage are capable of forming hypotheses and deducing possible consequences, allowing them to construct their own mathematics and develop abstract thought patterns using symbolic reasoning without the necessity of perceptive data. Reasoning skills within this stage include clarification, inference, evaluation, and application. Application allows for and benefits from connections between mathematical concepts to real-life situations.
How Math in Focus Delivers
Math in Focus features problematized content rooted in real world-contexts, making mathematical solutions relevant and connected to students’ own lives.
In 2000, the National Council of Teachers of Mathematics adopted a Communication Standard, which notes that “the communication process also helps build meaning and permanence for ideas and makes them public” (p. 60).
Mathematical discourse, or talking about mathematics, is viewed as an increasingly important way for students to learn and make sense of mathematics. Through classroom discourse, which includes listening and speaking, all aspects of mathematical thinking can be discussed, dissected, and understood. Dialogue in the classroom provides access to ideas, relationships among those ideas, strategies, procedures, facts, mathematical history, and more (Chapin, O’Connor, & Canavan Anderson, 2009).
One phrase used to describe a classroom in which communication and discussion are primary vehicles for learning is the “Math-Talk Learning Community.” Hufferd-Ackles, Fuson, and Sherin (2004) describe a math-talk learning community as one in which “individuals assist one another’s learning of mathematics by engaging in meaningful mathematics discourse” (p. 81).
“The informal and formal representations and experiences need to be continually connected in a nurturing ‘math talk’ learning community, which provides opportunities for all children to talk about their mathematical thinking and produce and improve their use of mathematical and ordinary language” (Cross et al., 2009, p. 43).
Effective discourse in the classroom has been shown to increase learning and achievement. Klibanoff, Levine, Huttenlocher, Vasilyeva, and Hedges (2006) conducted a study of how teachers’ use of language impacted students’ mathematical knowledge. To test this, the researchers transcribed teachers’ language use and found that the frequency of teachers’ math talk correlated with students’ increased mathematical knowledge. Hatano and Inagaki (1991) found that students who discussed and justified their solutions with peers demonstrated greater mathematical understanding than students who did not engage in such discussions. Leinwand and Fleischman (2004) reviewed research on effective math instruction and concluded that talking about math and explaining the rationale for solutions builds conceptual understanding.
A math-talk community has been found to be beneficial with English learners (Hufferd-Ackles et al., 2004). They found that creation of a math-talk community requires teachers to move from the level of a traditional, teacher-directed classroom to a classroom in which teachers coach and assist as students take leading roles. To do so, students need to develop skills across the components of questioning, explaining mathematical thinking, identifying the source of mathematical ideas, taking responsibility for learning, and mathematical representations.
Communication appears to help students persist in solving problems and to increase motivation and engagement. Research has also shown that learners are engaged in the learning process when they are asked to explain and reflect on their thinking processes (Good & Whang, 1999; Hettich, 1976; Surbeck,1994). Continuing to work with students by asking them to explain and justify how they solved problems helps to maintain student engagement (NRC, 2001).
Classroom discussions can be organized in ways that have been shown to support the acquisition of mathematics concepts and language development (Smith & Stein, 2011). Asking “why?” and “how do you know?” is one strategy that effective teachers use to encourage students to explain their thinking, solve problems, and share mathematical strategies and ideas with their peers (Clements & Sarama, 2008; Thomson, Rowe, Underwood, & Peck, 2005). Instructional practices including restating, prompting students, and engaging in whole-class discussion, small-group discussion, and paired conversations have been shown to be effective in improving student understanding (Chapin et al., 2009).
Discourse also provides teachers with opportunities for assessment. “Mathematical conversations provide opportunities for teachers to hear regularly from their students and to learn about the range of ideas students have about a particular mathematical idea, the details supporting students’ ideas, the values students attach to those ideas, and the language students use to express those ideas. The knowledge teachers gain from engaging with their students in conversations is essential for teaching for understanding” (Franke et al., 2007, p. 237).
How Math in Focus Delivers
Math in Focus supports teachers in fostering a Math Talk Learning Community that engages and guides students in productive, collaborative speaking and listening. Math Talk features within the program build on students’ thinking and provide opportunities for students to share, analyze, and compare ideas to develop their conceptual understanding.
To help all students learn to think mathematically, teachers must meet them where they are. As Vygotsky (1978) noted in his seminal research, when teachers assess students’ current understanding and teach new concepts, skills, and strategies at an according level, instruction takes place within students’ ‘zones of proximal development’ –which yields optimal learning.
Dacey, Lynch, and Salemi (2013) describe differentiation as “a philosophy of teaching based on the belief that all learners are different and that all students are capable of learning” (pp. 5–6). In the classroom, teachers encounter students who are on grade, above grade, below grade—as well as English learners, students with special needs, students who are gifted, and students with varying learning styles and cultural backgrounds. In the mathematics classroom, “mathematics instructors must respond to the diverse needs of individual students . . . using differentiated instruction, a process of proactively modifying instruction based on students’ needs” (Chamberlin & Powers, 2010, p. 113).
Differentiating instruction is an organized but flexible way to alter teaching to help all students maximize their learning (Tomlinson, 1999) and is necessary in order to meet the needs of all learners in today’s diverse classrooms (Tomlinson, 2000). As Tomlinson (2001), a leading researcher on the topic, explains, to differentiate instruction, teachers can adjust the content of what is being learned, adjust the process of learning (by providing additional supportive strategies, for example, or adjusting pacing), and tailor the expected outcomes (assessments, products, or tasks) of how learning is assessed. Tomlinson and Allan (2000) purport that in order for learning to take place, activities must be at the right level for the learner.
Research demonstrates the benefits of differentiation. In a study of numerous teachers using differentiated instruction, researchers found that students felt learning was more relevant; students were motivated to stay engaged in learning; students experienced greater success; students felt greater ownership of content, products, and performances; and teachers gained new insights (Stetson, Stetson, & Anderson, 2007).
Effective tools and strategies for differentiating instruction and offering intervention as needed are particularly crucial in today’s diverse classrooms. In a single classroom, students may have diverse cultures, speak different languages, and differ in their prior knowledge, readiness, skills, motivations, interests, and learning styles (Tomlinson, 2005). These differences matter on so many levels, because “Research has identified consistent, average differences in mathematics competence and performance depending on membership in a particular social group” (Cross, et al., 2009, p. 101). These differing needs must be effectively addressed. Teachers must help all students achieve, as noted in the Principles to Actions: Ensuring Mathematical Success for All from National Council of Teachers of Mathematics (2014, p. 60):
Support for access and equity requires, but is not limited to, high expectations, access to high-quality mathematics curriculum and instruction, adequate time for students to learn, appropriate emphasis on differentiated processes that broaden students’ productive engagement with mathematics, and human and material resources. Equity in school mathematics outcomes is often conflated with equality of inputs. Providing all students the same curricular materials, the same methods of teaching, the same amount of instructional time, and the same school-based supports for learning is different from ensuring that all students, regardless of background characteristics, have the same likelihood of achieving meaningful outcomes (Gutiérrez, 2013).
How Math in Focus Delivers
Math in Focus offers differentiated material for struggling students, on-level students, and advanced students. Reteach activities are designed for Extra Support and directly correlate to each Independent Practice in the chapter. Examples are provided for each set of questions to guide students and scaffold their understanding. The questions provide more exposure to concepts or skills. Additionally, the Math in Focus Teacher Edition provides tips for helping students at point of use.
Extra Practice and Homework are designed for On-Level students. Put On Your Thinking Cap! Questions are included to provide added challenge and more exposure to higher-order thinking activities. Enrichment activities advance students’ thinking and provide challenge while honing critical and creative thinking.
Language Development gives tips and suggestions for reinforcing vocabulary for English Language Learners.
“An excellent mathematics program ensures that assessment is an integral part of instruction, provides evidence of proficiency with important mathematics content and practices, includes a variety of strategies and data sources, and informs feedback to students, instructional decisions, and program improvement” (NCTM, 2014, p. 89).
Monitoring student progress is essential in the classroom. Assessments “permit the teacher to grasp students’ preconceptions, which is critical to working with and building on those notions. Once the knowledge to be learned is well defined, assessment is required to monitor student progress (in mastering concepts as well as factual information), to understand where students are in the developmental path from informal to formal thinking, and to design instruction that is responsive to student progress” (Donovan & Bradford, 2005, p. 16).
Ongoing, formative, informal, and formal assessment data are essential for meeting the needs of all students, identifying when instruction has been successful and when additional support, intervention, or challenge opportunities are needed. Summative data provide essential benchmark data for results and future planning. As reported across an abundant research base, the regular use of assessment to monitor student progress can mitigate and prevent mathematical weaknesses and improve student learning (Clarke & Shinn, 2004; Fuchs, 2004; Hattie, 2012; Lembke & Foegen, 2005; NCTM, 2014; Popham, 2008; Skiba, Magnusson, Marston, & Erickson, 1986).
As Baker, Gersten, and Lee (2002) report from their meta-analysis “One consistent finding is that providing teachers and students with specific information on how each student is performing seems to enhance mathematics achievement consistently” (p. 67). Similarly, the National Mathematics Advisory Panel (2008) points out “teachers’ regular use of formative assessment improves students’ learning” (p. xxiii) and “use of formative assessments benefited students at all ability levels” (p. 46).
The phrase “formative assessment” encompasses the wide variety of activities—formal and informal—that teachers employ throughout the learning process to gather data to assess student understanding and to make and adapt decisions to improve instruction. Formative assessment is not an end; it is a means, to guide teaching and learning as it occurs (Black & Wiliam, 1998; Shepard, 2000; Heritage, 2007).
Effective assessment tools allow teachers to collect data about what is working—and what is not—so that they can take precise, swift, and effective action in meeting the specific needs of students. For this reason, using varied item types and tasks may be the best way to get an accurate, complete reflection of student understanding; “Using multiple types of assessments provides more insight into students’ learning because students have more than one way to demonstrate their knowledge and skills” (McREL, 2010, p. 44).
In defining the elements of an effective student assessment system, Darling-Hammond (2010) said that such a system must “address the depth and breadth of standards as well as all areas of the curriculum, not just those that are easy to measure” (p. 1).
For students, too, assessment is key to learning. The feedback students receive from assessment helps them to evaluate their strengths and weaknesses, and gauge their progress toward meeting learning goals; formative assessment has a positive effect on learning (Black & Wiliam, 1998; Hattie, 2012; Jerald, 2001).
Teachers should examine incorrect student responses to see if they reveal specific student misunderstandings (Popham, 2008). By analyzing student errors, teachers can determine which specific concepts, algorithms, or procedures need additional instruction (Ketterlin-Geller & Yovanoff, 2009).
An additional benefit of formative assessment is that it has been shown to be particularly helpful to lower-performing students. Gersten and Clarke (2007) concluded that “the use of ongoing formative assessment data invariably improved mathematics achievement of students with mathematics disability” (p. 2). As a result, formative assessments can minimize achievement gaps while raising overall achievement (Black & Wiliam, 1998). The National Research Council’s (1999) Testing, Teaching, and Learning, which focuses on Title I students, recommends that “Teachers should administer assessments frequently and regularly in classrooms for the purpose of monitoring individual students’ performance and adapting instruction to improve their performance” (p. 47).
“When viewed as a process that is indistinguishable from effective instruction, assessment serves as a means to achieve productive teaching and learning for all, rather than merely as the final stage in the traditional teach learn assess cycle” (NCTM, 2014, p. 94).
How Math In Focus Delivers
Monitoring students’ learning with meaningful assessment is an essential part of planning effective instruction that will meet the specific needs of all students. Assessment opportunities in Math in Focus offer a complete picture of student progress by employing numerous and broad-ranging measurements to evaluate students’ mathematical development in both the short- and long-term.
Math in Focus offers a rich array of assessment opportunities throughout the instructional pathway and in a variety of formats, both print and digital. Some Math in Focus assessments are only available in paper-and-pencil format to allow students to model flexibly with their CPA toolbox and the teacher to see students’ work and thinking. Digital assessments are auto-scored, providing rich data and reporting to inform grouping for differentiation. Administering Math in Focus digital assessments via Ed: Your Friend in Learning® empowers teachers by providing access to various reports full of rich data that can be further drilled down into for deeper insights on students’ performance.
The Formative and Benchmark assessments are available in both paper-and-pencil and digital formats. Because they are auto-scored, digital versions of the Formative and Benchmark assessment items may be slightly different from paper-and-pencil versions while assessing the same objectives.
Formative Assessments
Formative assessments, available within the Student Edition and digitally via Ed: Your Friend in Learning, enable teachers to efficiently and effectively deliver instruction and assign differentiated resources.
Independent Practice helps students consolidate their learning at the end of each section in a chapter. Based on their performance here, teachers can form small groups using differentiation resources to support, reinforce, or enrich learning.
Quick Checks are pre-chapter quizzes that evaluate students’ understanding of prerequisite concepts and skills.
The Chapter Review at the end of each chapter consolidates students’ learning. Within the Chapter Review, several Assessment Prep items are provided that are specifically geared toward state tests.
Summative Assessments
In the Assessment Guide, the Chapter Test for each chapter serves as a review of concepts learned and as a way to see students’ thinking.
The Cumulative Review provides the opportunity for consolidation of concepts and skills across multiple chapters.
The Mid-Year and End-of-Year Benchmark Assessments are administered in Grade 3 through Course 3. They are located in both the Assessment Guide Teacher Edition and digitally via Ed: Your Friend in Learning to ensure that students do not see the questions before taking the tests.
Performance Tasks
Students demonstrate their knowledge, understanding, and proficiency by completing Performance Tasks at the end of each chapter in the Student Edition. A rubric is provided for teachers to give students feedback on their performance and to show them evidence of their progress.
Singapore has placed at the top in the last four administrations of the Trends in International Math and Science Study (TIMSS); the Singapore Math® program is largely believed to be responsible for this exceptional performance. Math in Focus addresses those key evidence-based features in the Singapore Math® program that have made the program so successful, and presents these features in a version of the program specifically designed to meet the needs of American students and educators.
Research in cognition generally and in mathematics education specifically supports the many features that characterize Math in Focus. The program employs the strategic development of concepts throughout the current grade and successive grades to allow for a deeper understanding of the skills without unnecessary repetition. Extensive practice opportunities allow for skill review both before and during lessons, and for the applications of concepts and skills to new contexts. Deliberate scaffolding supports the development of students’ reasoning skills as they work on successively more intricate math problems and move from solving simple routine problems to independently solving complex, nonroutine word problems.
By using evidence-based teaching and learning strategies and a curriculum model demonstrated by research to be effective, Math in Focus prepares students for future learning in mathematics and develops the problem solving and critical thinking skills needed in the 21st century.
Agrawal, J., & Morin, L. (2016). Evidence-based practices: Applications of concrete representational abstract framework across math concepts for students with mathematics disabilities. Learning Disabilities Research & Practice, 31(1), 34–44.
Alberti, S. (2013). Making the shifts. Educational Leadership, 70(4), 24-27.
Baker, S., Gersten, R., & Lee, D. (2002). A synthesis of empirical research on teaching mathematics to low-achieving students. The Elementary School Journal, 103(1), 67.
Ball, D. L. (1992a). Constructing new forms of teaching: Subject matter knowledge in inservice teacher education. Journal of Teacher Education, 43(5), 347–356.
Ball, D. L. (1992b). Magical hopes: Manipulatives and the reform of math education. American Educator, 16(2), 14–18 46–7.
Baxter, J., Woodward, J., & Olson, D. (2005). Writing in mathematics: An alternative form of communication for academically low-achieving students. Learning Disabilities Research & Practice, 20, 119–135.
Beane, J. A. (1997). Curriculum integration: Designing the core of democratic education. Alexandria, VA: Association for Supervision and Curriculum Development.
Bell, S. (2010) Project-based learning for the 21st century: Skills for the future. The Clearing House: A Journal of Educational Strategies, Issues and Ideas, 83(2), 39–43.
Berninger, V. W., & Richards, T. L. (2002). Brain literacy for educators and psychologists. Cambridge, MA: Academic Press.
Black, L. S., Trzesniewski, K., & Dweck, C. S. (2007). Implicit theories of intelligence predict achievement across an adolescent transition: A longitudinal study and an intervention. Child Development, 78(1), 246–263.
Black, P., & Wiliam, D. (1998). Assessment and classroom learning. Assessment in Education: Principles, Policy, and Practice, 5(1), 7–73.
Blank, L. (2000). A metacognitive learning cycle: A better warranty for student understanding. Science Education, 84(4), 486–506.
Blatto-Vallee, G., Kelly, R., Gaustad, M., Porter, J., & Fonzi, J. (2007). Visual spatial representation in mathematical problem solving by deaf and hearing students. Journal of Deaf Students and Deaf Education, 12(4), 432–48.
Blumenfeld, P. C., Kempler, T. M., & Krajcik, J. S. (2006). Motivation and cognitive engagement in learning environments. In R. K. Sawyer (Ed.), The Cambridge handbook of the learning sciences (pp. 475–488). New York, NY: Cambridge University Press.
Boaler, J. (2011). Changing students’ lives through the de-tracking of urban mathematics classrooms. Journal of Urban Mathematics Education, 4(1), 7–14.
Boaler, J. (2013). Ability and mathematics: The mindset revolution that is reshaping education. Forum, 55(1). 143-150.
Boaler, J. (2016). Mathematical mindsets. Hoboken, NJ: Wiley Press.
Boaler, J., & Staples, M. (2008). Creating mathematical futures through an equitable teaching approach: The case of Railside School. Teachers College Record, 110(3), 608–645.
Bobis, J., & Way, J. (2018). Building connections between children’s representations and their conceptual development in mathematics. In V. Kinnear, M. Lai, &, T. Muir (Eds.), Forging connections in early mathematics teaching and learning (pp. 55–72). Singapore: Springer.
Booth, J. L., Lange, K. E., Koedinger, K. R., & Newton, K. J. (2013). Using example problems to improve student learning in algebra: Differentiating between correct and incorrect examples. Learning and Instruction, 25(2), 24–34.
Bosse, M., & Faulconer, J. (2010). Learning and assessing mathematics through reading and writing. School Science and Mathematics, 108(1), 8–19.
Boston, M. D., & Wilhelm, A. G. (2015). Middle school mathematics instruction in instructionally focused urban districts. Urban Education, 1–33.
Brandenburg, M. L. (2002). Advanced math? Write! Educational Leadership, 60(3), 67–68.
Bransford, J. D., Brown, A. L., & Cocking, R. R. (Eds.). (2000). How people learn: Brain, mind, experience, and school. Washington, DC: National Academy Press.
Bray, W. S., Dixon, J. K., & Martinez, M. (2006). Fostering communication about measuring area in a transitional language class. Teaching Children Mathematics, 13(3), 132–138.
Bruner, J. S. (1966). Toward a theory of instruction. Cambridge, MA: Belkapp Press.
Bruner, J. (1979). On knowing: Essays for the left hand. Cambridge, MA: Harvard University Press.
Bryant, C. (2015). Mathematical habits of mind. Edutopia. Retrieved online: https://www.edutopia.org/blog/mathematical-habits-of-mind-cindy-bryant
Bybee, R. W, Taylor, J. A., Gardner, A., Van Scotter, P., Powell, J. C., Westbrook, A., & Landes, N. (2006). The BSCS 5E instructional model: Origins and effectiveness. Colorado Springs, CO: BSCS.
Cai, J., & Nie, B. (2007). Problem solving in Chinese mathematics education: Research and practice. Mathematics Education, 39, 459–473.
Caine, R. N., & Caine, G. (1994). Making connections: Teaching and the human brain. Alexandria, Virginia: Association for Supervision and Curriculum Development.
Campbell, K. J., Collis, K. F., & Watson, J. M. (1996). Visual processing during mathematical problem solving. Educational Studies in Mathematics, 28, 177–194.
Capraro, R., & Slough, S. (2013). Why PBL? Why stem? Why now?. In R. Capraro, M. Capraro, & J. Morgan (Eds.), An introduction to STEM project-based learning: An integrated science, technology, engineering, and mathematics approach (pp. 1–6). Rotterdam: Sense Publishers.
Carpenter, T. P., Fennema, E., Franke, M. L., Levi, L., & Empson, S. B. (2015). Children’s mathematics. Cognitively guided instruction. Portsmouth, NH: Heinemann.
Chamberlin, M. T., & Powers, R. A. (2010). The promise of differentiated instruction for enhancing the mathematical understandings of college students. Teaching Mathematics and its Applications: An International Journal of the Institute of Mathematics and its Applications, 29(3), 113–139.
Chapin, S. H., O’Connor, C., & Canavan Anderson, N. (2009). Classroom discussions: Using math talk to help students learn, grades K–6 (2nd Ed.). Sausalito, CA: Math Solutions.
Clarke, B., & Shinn, M. R. (2004). A preliminary investigation into the identification and development of early mathematics curriculum-based measurement. School Psychology Review, 33(2), 234–248.
Clements, D. (1999). “Concrete” manipulatives, concrete ideas. Contemporary Issues in Early Childhood, 1(1), 45–60.
Clements, D. H., & McMillen, S. (1996). Rethinking “concrete” manipulatives. Teaching Children Mathematics, 2(5), 270–27.
Clements, D. H., & Sarama, J. (2007). Effects of a preschool mathematics curriculum: Summative research on the “Building Blocks” project. Journal for Research in Mathematics Education, 38(2), 136–163.
Clements, D. H., & Sarama, J. (2008). Experimental evaluation of the effects of a research-based preschool mathematics curriculum. American Educational Research Journal, 45(2), 443–494.
Cross, C. T., Woods, T. A., & Schweingruber, H. (Eds.). (2009). Mathematics learning in early childhood: Paths toward excellence and equity. Center for Education, Division of Behavioral and Social Science and Education. Washington, DC: National Academy Press.
Cuoco, A., Goldenberg, E. P., & Mark, J. (1996). Habits of mind: An organizing principle for mathematics curricula. Journal of Mathematical Behavior, 15(4), 375–402.
Czerniak, C. M., Weber, W. B., Jr., Sandmann, A., & Ahem, J. (1999). A literature review of science and mathematics integration. School Science & Mathematics, 99(8), 421–430.
Dacey, L., Lynch, J., & Salemi, R. (2013). How to differentiate your math instruction: Lessons, ideas, and videos with Common Core support: A multimedia professional learning resource. Sausalito, CA: Math Solutions.
Darling-Hammond, L. (2010). Performance counts: Assessment systems that support high-quality learning. Washington, DC: Council of Chief State School Officers.
David, J. & Greene, D. (2007). Improving Mathematics Instruction in Los Angeles High Schools: An Evaluation of the PRISMA Pilot Program. Palo Alto, Calif.: Bay Area Research Group.
Dienes, Z. (1971). Building up mathematics (4th Ed.). London, UK: Hutchinson Educational Ltd.
Dienes, Z. (1973). A theory of mathematics learning. In F. J. Crosswhite, J. Higgins, A. Osborne, & R. Shunway (Eds.) Teaching mathematics: Psychological foundations (pp. 137–148). Columbus, OH: Charles A. Jones Publishing.
Dixon, J. (2018). Just-in-time vs. just-in-case scaffolding: How to foster productive perseverance. Retrieved online: /blog/just-in-time-vs-just-in-case-scaffolding-how-to-foster-productive-perseverance
Donovan, S., & Bransford, J. (2005). How students learn: mathematics in the classroom. Washington, DC: National Research Council.
Dweck, C. (2006). Mindset: The new psychology of success. New York: Random House.
Dweck, C. (2008). Mindsets and math/science achievement. New York: Carnegie Corporation of New York Institute for Advanced Study.
Fan, L. & Zhu, Y. (2007). Representation of problem-solving procedures: A comparative look at China, Singapore, and US mathematics textbooks. Educational Studies of Mathematics, 66, 61–75.
Feldman, K., & Kinsella, K. (2008). Narrowing the language gap: The case for explicit vocabulary instruction in secondary classrooms. In L. Denti & G. Guerin (Eds.), Effective practices for adolescents with reading and literacy challenges (pp. 3–24). New York, NY: Routledge.
Fennema, E., Carpenter, T. P., & Lamon, S. J. (Eds.). (1991). Integrating research on teaching and learning mathematics. Albany, NY: State University of New York Press, 231.
Fong H. K. (1993). Bridging the gap between secondary and primary mathematics. Teaching and Learning, 14(2) 73–84.
Fosnot, C. T., & Dolk, M. (2001). Young mathematicians at work: Constructing multiplication and division. Portsmouth, NH: Heinemann.
Franke, M. L., Kazemi, E., & Battey, D. (2007). Understanding teaching and classroom practice in mathematics. In F. K. Lester (Ed.), Second handbook of research on mathematics teaching and learning: A project of the National Council of Teachers of Mathematics (pp. 225–256). Charlotte, NC: Information Age Publishing.
Fuchs, L. S. (2004). The past, present, and future of curriculum-based measurement research. School Psychology Review, 33, 188–192.
Fuchs, L. S., Fuchs, D., & Prentice, K. (2004). Responsiveness to mathematical problem-solving instruction: Comparing students at risk of mathematics disability with and without risk of reading disability. Journal of Learning Disabilities, 37(4), 293–306.
Furner, J. M., & Duffy, M. L. (2002). Equity for all students in the new millennium: Disabling math anxiety. Intervention in School and Clinic, 38, 67–74.
Fuson, K.C., Atler, T., Roedel, S., & Zaccariello, J. (2009). Building a nurturing, visual, math-talk teaching-learning community to support learning by English language learners and students from backgrounds of poverty. New England Mathematics Journal, XLI(May), 6–16.
Fuson, K. C., Smith, S. T., & Lo Cicero, A. (1997). Supporting Latino first graders’ ten-structured thinking in urban classrooms. Journal for Research in Mathematics Education, 28(6), 738–766.
Gersten, R., Beckmann, S., Clarke, B., Foegen, A., Marsh, L., Star, J. R., & Witzel, B. (2009). Assisting students struggling with mathematics: Response to intervention (RtI) for elementary and middle schools. Institute of Education Sciences What Works Clearinghouse. Washington, DC: U.S. Department of Education. Retrieved online: http://ies.ed.gov/ncee/wwc/pdf... pg_042109.pdf
Gersten, R., & Chard, D. (2001). Number sense: Rethinking arithmetic instruction for students with mathematical disabilities. LD OnLine. Retrieved online: http:// www.ldonline.org/article/5838/
Gersten, R., & Clarke, B.S. (2007). Effective strategies for teaching students with difficulties in mathematics. Instruction Research Brief. Reston, VA: National Council of Teachers of Mathematics.
Gersten, R., Clarke, B., & Mazzocco, M. M. (2007). Historical and contemporary perspectives on mathematical learning disabilities. In D. Berch & M. M. Mazzocco (Eds.), Why is math so hard for some children? The nature and origins of mathematical learning difficulties and disabilities (pp. 7–27). Baltimore, MD: Brookes Publishers.
Ginsberg, A., Leinwand, S., Anstrom, T., & Pollock, E. (2005). What the United States can learn from Singapore’s world-class mathematics system (and what Singapore can learn from the United States): An exploratory study. Washington, DC: American Institutes for Research.
Gningue, S. (2006). Students working between and within representations: An application of Dienes’s principles. For the Learning of Mathematics, 26(2), 41–47.
Goldenberg, E., Mark, J., Kang, J., Fries, M., Carter, C., & Cordner, T. (2015). Making sense of algebra: Developing students’ mathematical habits of mind. Portsmouth, NH: Heinemann.
Good, J. M., & Whang, P. A. (1999). Making meaning in educational psychology with student response journals. Paper presented at the annual meeting of the American Educational Research Association, Montreal, Canada.
Gu, F., Huang, R., & Gu, L. (2017). Theory and development of teaching through variation in mathematics in China. In R. Huang & Y. Li (Eds.), Teaching and learning mathematics through variation (pp. 13–41). Boston, MA: Sense Publishers.
Gu, L., Hunag, R., & Marton, F. (2004). Teaching with variation: A Chinese way of promoting effective mathematics learning. In L. Fan, N. Wong, J. Cai, & S. Li (Eds.), How Chinese learn mathematics: Perspectives from insiders (pp. 309–347). Singapore: World Scientific Publishing Co. Pte. Ltd.
Gutiérrez , R. (2013). The sociopolitical turn in mathematics education. Journal for Research in Mathematics Education, 44(1), 37–68.
Guthrie, J. T., & Humenick, N. M. (2004). Motivating students to read: Evidence for classroom practices that increase reading motivation and achievement. In P. McCardle, & V. Chhabra (Eds.) The voice of evidence in reading research (pp. 329–354).. Baltimore, MD: Paul H Brookes Publishing.
Han, S., Capraro, R., & Capraro, M. (2014). How science, technology, engineering, and mathematics (STEM) project-based learning (PBL) affects high, middle, and low achievers differently: The impact of student factors on achievement. International Journal of Science and Mathematics Education, 13(5), 1089–1113.
Har, Y. B. (2005). Building foundations and developing creativity: An analysis of Singapore mathematics textbooks. Nanyang, Singapore: National Institute of Education, Nanyang Technological University.
Hatano, G., & Inagaki, K. (1991). Constrained person analogy in young children’s biological inference. Cognitive Development, 6(2), 219–231.
Hattie, J. (2012). Visible learning for teachers: Maximizing impact for learning. New York: Routledge.
Heritage, M. (2007). Formative assessment: What do teachers need to know and do? Phi Delta Kappan, 89(2), 140–145.
Hettich, P. (1976). The journal: An autobiographical approach to learning. Teaching of Psychology, 3(2), 60–63.
Hibbard, M. (1996). A teacher’s guide to performance-based learning and assessment. Alexandria, VA: ASCD.
Hidi, S., & Boscolo, P. (2006). Motivation and writing. In .A. MacArthur, S. Graham, & J. Fitzgerald (Eds.), Handbook of writing research (pp. 144–157). NY: The Guilford Press.
Hiebert, J., Carpenter, T. P., Fennema, E., Fuson, K., Human, P., Murray, H., Olivier, A., & Wearne, D. (1996). Problem solving as a basis for reform in curriculum and instruction: The case of mathematics. Educational Researcher, 25(4), 12–21.
Hiebert, J., & Grouws, D. A. (2007). The effects of classroom mathematics teaching on students’ learning. In F. K. Lester (Ed.), Second handbook of research on mathematics teaching and learning: A project of the National Council of Teachers of Mathematics (pp. 371–404). Charlotte, NC: Information Age Publishing.
Hiebert, J., Morris, A. K., Berk, D., & Jansen, A. (2007). Preparing teachers to learn from teaching. Journal of Teacher Education, 58(1), 47–61.
Hill, M., Sharma, M., O’Byrne, J., & Airey, J. (2014). Developing and evaluating a survey for representational fluency in science. International Journal of Innovation in Mathematics and Science Education, 22(6). Retrieved online: https://openjournals.library.sydney.edu.au/index.php/CAL/article/view/7484
Ho, K. F., Teong, S. K., & Hedberg, J. G. (2004). Creating problem solving repertoires. In Proceedings of the Tenth International Congress on Mathematical Education (pp. 1–6). Roskilde, Denmark: Roskilde University
Hoven, J., & Garelick, B. (2007). Singapore Math: Simple or complex. Educational Leadership, 65(3), 28–31.
Huang, R., & Li, Y. (2017). Teaching and learning mathematics through variation: Confucian heritage meets western theories. Boston, MA: Sense Publishers.
Huat, J. N. C., Huat, L. K. (2006). A handbook for mathematics. Singapore: Marshall Cavendish Education.
Hufferd-Ackles, K., Fuson, K. C., & Sherin, M. G. (2004). Describing levels and components of a math-talk learning community. Journal for Research in Mathematics Education, 35(2), 81–116.
Hui, C. S., Hoe, L. N., & Lee, K. P. (2017). Teaching and learning with concrete-pictorial-abstract sequence: A proposed model. The Mathematics Educator, 17(1), 1–28.
Janzen, J. (2008). Teaching English language learners in the content areas. Review of Educational Research, 78(4), 1010-1038.
Jerald, C. D. (2001). Dispelling the myth revisited. Washington DC: Education Trust.
Jitendra, A. K., Dupuis, D. N., Rodriguez, M. C., Zaslofsky, A. F., Slater, S., Cozine-Corroy, K., & Church, C. (2013). A randomized controlled trial of the impact of schema-based instruction on mathematical outcomes for third-grade students with mathematics difficulties. The Elementary School Journal, 114(2), 252–276.
Johnson, K., Herr, T. & Kysh, J. (2004). Crossing the river with dogs: Problem solving for college students. Emeryville, CA: Key College Publishing.
Jordan, L., Miller, M., & Mercer, C. (1998). The effects of concrete to semi-concrete to abstract instruction in acquisition and retention of fraction concepts and skills. Learning Disabilities: A Multidisciplinary Journal, 9, 115–122.
Kapur, M. (2010). Productive failure in mathematical problem solving. Instructional Science, 38(6), 523–550.
Ketterlin-Geller, L. R., & Yovanoff, P. (2009). Diagnostic assessments in mathematics to support instructional decision making. Practical Assessment, Research & Evaluation, 14(16), 1–11.
Klibanoff, R. S., Levine, S. C., Huttenlocher, J., Vasilyeva, M., & Hedges, L. V. (2006). Preschool children’s mathematical knowledge: The effect of teacher ‘math talk.’ Developmental Psychology, 42(1), 59–69.
Krajcik J., & Blumenfeld, P. (2006). Project-based learning. In R Keith (Ed.), The Cambridge handbook of the learning sciences (pp. 317–334).. New York, NY: Cambridge University Press.
Lawson, A. (2001). Using the learning cycle to teach biology concepts and reasoning patterns. Journal of Biological Education, 35(4), 165–169.
Land, M. (2013). Full STEAM ahead: The benefits of integrating the arts into STEM. Procedia Computer Science, 20, 547–552.
Leinwand, S., & Fleischman, S. (2004). Teach mathematics right the first time. Educational Leadership, 62(1), 88–89.
Lembke, E., & Foegen, A. (2005). Identifying indicators of early mathematics proficiency in kindergarten and Grade 1. (Technical Report No. 6). Minneapolis: University of Minnesota. College of Education and Human Development. Retrieved online: www.progressmonitoring.org/ pdf/TREarlymath6.pdf
Leong, Y. H., Ho, W. K., & Cheng, L. P. (2015). Concrete-pictorial-abstract: Surveying its origins and charting its future. The Mathematics Educator, 16(1), 1–19.
Lesh, R., & Zawojewski, J. S. (2007). Problem solving and modeling. In F. K. Lester (Ed.), Second handbook of research on mathematics teaching and learning: A project of the National Council of Teachers of Mathematics, (pp. 763–804) Charlotte, NC: Information Age Publishing.
Lovitt, T. C., & Curtiss, K. A. (1968). Effects of manipulating an antecedent event on mathematics response rate. Journal of Applied Behavior Analysis, 1(4), 329–333.
Marzano, R. J., Pickering, D. J., & Pollock, J. E. (2001). Classroom instruction that works: Research-based strategies for increasing student achievement. Alexandria, VA: Association for Supervision and Curriculum Development (ASCD).
McTighe, J., & Wiggins, G. P. (2013). Essential questions: opening doors to student understanding. Alexandria, Virginia, USA: ASCD.
Merritt, J., Lee, M., Rillero, P., & Kinach, B. M. (2017). Problem-based learning in k–8 mathematics and science education: A literature review. Interdisciplinary Journal of Problem-Based Learning, 11(2).
Michaels, S., O’Connor, C., & Resnick, L. (2008). Deliberative discourse idealized and realized: Accountable talk in the classroom and in civic life. Studies in Philosophy and Education, 27(4), 283–297.
Mid-Continent Research for Education and Learning (McREL). (2010). What we know about mathematics teaching and learning, third edition. Bloomington, IN: Solution Tree Press.
Miller, S. P., & Hudson, P. J. (2007). Using evidence-based practices to build mathematics competence related to conceptual, procedural, and declarative knowledge. Learning Disabilities Research & Practice, 22(1), 47–57.
Miri, B., David, BC., & Uri, Z. (2007). Purposely teaching for the promotion of higher-order thinking skills: A case of critical thinking. Research in Science Education, 37(4), 353–369.
Mondada, L., & Doehler, S. P. (2004). Second language acquisition as situated practice: Task accomplishment in the French second language classroom. The Modern Language Journal, 88, 501–518.
Mullis, I. V. S., Martin, M. O., Foy, P., & Hooper, M. (2016). TIMSS 2015 International Results in Mathematics. Retrieved from Boston College, TIMSS & PIRLS International Student Center website: http://timssandpirls.bc.edu/ti... Center for Education Statistics (NCES). (2017). The TIMSS Math and Science Assessments. Retrieved online: https://nces.ed.gov/timss/tims... Council of Teachers of Mathematics (NCTM). (2000). Principals and standards for school mathematics. Reston, VA: Author. Retrieved online: http://www.nctm.org/ standards
National Council of Teachers of Mathematics (NCTM). (2006). Curriculum focal points for prekindergarten through grade 8 mathematics. Reston, VA: Author.
National Council of Teachers of Mathematics (NCTM). (2014). Principles to actions: Ensuring mathematical success for all. Reston, VA: Author.
National Mathematics Advisory Panel. (2008). Foundations for success: The final report of the National Mathematics Advisory Panel. Washington, DC: U.S. Department of Education. Retrieved online: http://www2.ed.gov/about/bdscomm/list/mathpanel/index.html
National Research Council (NRC). (1999). R. F. Elmore & R. Rothman (Eds.), Testing, teaching, and learning: A guide for states and districts. Commission on Behavioral and Social Sciences, Committee on Title I Testing and Assessment, National Research Council. Washington, DC: National Academy Press.
National Research Council (NRC). 2000. How people learn: Brain, mind, experience, and school: Expanded edition. Washington, DC: The National Academies Press. https://doi.org/10.17226/9853<... Research Council (NRC). (2001). Adding it up: Helping children learn mathematics. J. Kilpatrick, J. Swafford, & B. Findell (Eds.). Mathematics Learning Study Committee, Center for Education, Division of Behavioral and Social Science and Education. Washington, DC: The National Academies Press.
National Research Council (NRC). 2005. How students learn: History, mathematics, and science in the classroom. Washington, DC: The National Academies Press. https://doi.org/10.17226/10126
Ng, L. W. (2008). Problem solving heuristics for primary school mathematics: A comprehensive guide. Singapore: Pearson Prentice Hall.
Ojose, B. (2008). Applying Piaget’s theory of cognitive development to mathematics instruction. The Mathematics Educator, 18(1), 26–30.
Ozsoy, G., Memis, A., & Temur, T. (2009). Metacognition, study habits and attitudes. International Electronic Journal of Elementary Education, 2(1). Retrieved online: https://pdfs.semanticscholar.org/17e1/d8e43b657ce57d2d073e6c79405a1ff65bbc.pdf
Parker, C. (2015). Research shows how children and enjoy and succeed in math, Stanford expert says. Standford News. Retrieved from https://news.stanford.edu/2015/12/17/math-mindset-boaler-121725/
Polya, G. 1957. How to solve it: A new aspect of mathematical method (2nd ed.). Princeton, NJ: Princeton.
Polya, G. (1965). Mathematical discovery, volume II: On understanding, learning, and teaching problem solving. New York, NY: Wiley.
Polya, G. (1971). How to solve it. Princeton, NJ: Princeton University Press.
Popham, W. J. (2008). Transformative sssessment. Alexandria, VA: ASCD.
Pugalee, David K. (2005). Writing to develop mathematical understanding. Norwood, MA: Christopher-Gordon.
Russo, M., Hecht, D., Burghardt, M. D., Hacker, M., & Saxman, L. (2011). Development of a multidisciplinary middle school mathematics infusion model. Middle Grades Research Journal, 6(2), 113–128.
Sahlberg, P. (2011). Paradoxes of educational improvement: The Finnish experience. Scottish Educational Review, 43(1), 3–23.
Salingay, N. R., & Tan, D. A. (2018). Concrete-pictorial-abstract approach on students’ attitude and performance in mathematics. International Journal of Scientific & Technology Research, 7(5), 90–111.
Schroder, T., & Lester, F. (1989). Developing understanding in mathematics via problem solving. In P. Trafton (Ed), New directions for elementary school mathematics,1989 yearbook for the National Council of Teachers of Mathematics (pp. 31–42). Reston, VA: NCTM.
Schunk, D. H., Pintrich, P. R., & Meece, J. L. (2008). Motivation in education: Theory, research, and applications. Upper Saddle River, New Jersey: Pearson/Merrill Prentice Hall.
Shepard, L. A. (2000). The role of assessment in a learning culture. Educational Research, 29(7), 4–14.
Singapore Ministry of Education. (2012). Primary Mathematics Teaching and Learning Syllabus. Singapore: Curriculum Planning & Development Division. Retrieved online: https://fmsp.moe.edu.sg/qql/slot/u546/About%20Us/Departments/Mathematics/maths-primary-2013.pdf
Skiba, R., Magnusson, D., Marston, D., & Erickson, K. (1986) The assessment of mathematics performance in special education: Achievement tests, proficiency tests, or formative evaluation? Minneapolis: Special Services, Minneapolis Public Schools.
Smith, M., & Stein, M. (2011). 5 practices for orchestrating productive mathematics discussions (1st ed.). Reston, VA. National Council of Teachers of Mathematics.
Sousa, D. A. (2008). Recognizing and addressing mathematics difficulties. In How the brain learns mathematics (pp. 186–188). CA: Corwin Press.
Star, J. R. (2005). Reconceptualizing conceptual knowledge. Journal for Research in Mathematics Education, 36(5), 404–411.
Stein, M. K., & Lane, S. (1996). Instructional tasks and the development of student capacity to think and reason: An analysis of the relationship between teaching and learning in a reform mathematics project. Educational Research and Evaluation, 2(1), 50–80.
Stein, M. K., Remillard, J., & Smith, M. S. (2007). How curriculum influences student learning. In F. K. Lester (Ed.), Second handbook of research on mathematics teaching and learning: A project of the National Council of Teachers of Mathematics (pp. 319–370). Charlotte, NC: Information Age Publishing.
Stetson, R., Stetson, E., & Anderson, K. A. (2007). Differentiated instruction, from teachers’ experiences. The School Administrator, 8(64), online. Retrieved online: http://www.aasa.org/SchoolAdministratorArticle. aspx?id=6528
Stigler, J., & Hiebert, J. (1999). The teaching gap: Best ideas from the world’s teachers for improving education in the classroom. New York, NY: The Free Press.
Stylianou, D. A. (2011). An examination of middle school students’ representation practices in mathematical problem solving through the lens of expert work: Towards an organizing scheme. Educational Studies in Mathematics, 76, 265–280.
Stylianou, D. A., & Silver, E. A. (2004). The role of visual representations in advanced mathematical problem solving: An examination of expert-novice similarities and differences. Mathematical Thinking and Learning, 6(4), 353–387.
Surbeck, E. (1994). A glimpse through the door: Journal writing with preservice teachers. Childhood Education, 70(4), 232–235.
Taljaad, J. (2016). A review of multi-sensory technologies in a science, technology, engineering, arts and mathematics (STEAM) classroom, Journal of Learning Design, 9(2) 46–55.
Taylor, J., & McDonald, C. (2007) Writing in groups as a tool for non-routine problem solving in first year university mathematics, International Journal of Mathematical Education in Science and Technology, 38(5), 639–655.
Thompson, P. W., & Lambdin, D. (1994). Concrete materials and teaching for mathematical understanding. Arithmetic Teacher, (May), 556–558.
Thomson, S., Rowe, K., Underwood, C., & Peck, R. (2005). Numeracy in the early years: Project Good Start. Retrieved online: https://research.acer.edu.au/tll_misc/4
Thuneberg, H., Salmi, H., & Bogner, F. (2018). How creativity, autonomy, and visual reasoning contribute to cognitive learning in a STEAM hands-on inquiry-based module. Thinking Skills and Creativity, 29, 153–160.
Thuneberg, H., Salmi, H., & Fenyvesi, K. (2017). Hands-on math and art exhibition promoting science attitudes and educational plans. Education Research International, Article ID 9132791.
Tomlinson, C. A. (1999). The differentiated classroom: Responding to the needs of all learners. Alexandria, VA: Association for Supervision and Curriculum Development.
Tomlinson, C. A., (2000). Reconcilable differences: Standards- based teaching and differentiation. Educational Leadership, 58, 6–13.
Tomlinson, C. A., (2001). How to differentiate instruction in mixed-ability classrooms. (2nd ed.). Alexandria, VA: ASCD.
Tomlinson, C.A., (2005). Traveling the road to differentiation in staff development. Journal of Staff Development, 26, 8–12.
Tomlinson, C. A., & Allan, S. D. (2000). Leadership for differentiating schools and classrooms. Alexandria, VA: ASCD.
Van Garderen, D. (2006). Spatial visualization, visual imagery, and mathematical problem solving of students with varying abilities. Journal of Learning Disabilities, 39(6), 496–506.
Vygotsky, L. S. (1978). Mind in society: The development of higher psychological processes. Cambridge, MA: Harvard University.
Warshauwer, H. (2015). Productive struggle in middle school mathematics classrooms. Journal of Mathematics Teacher Education, 18(4), 375–400.
Watson, A., & Watson, G. (2013). Transitioning STEM to STEAM: Reformation of engineering education. The Journal for Quality & Participation. Retrieved online: https://www.academia.edu/8766909/Transitioning_STEM_to_STEAM_Reformation_of_Engineering_Education
Weiss, I., & Pasley, J. (2004). What is high-quality instruction? Educational Leadership, 61(5), 24–28.
Wiliam, D. (2011). Embedded formative assessment. Bloomington, IN: Solution Tree Press.
Yakman, G. (2008). STEAM Education: an overview of creating a model of integrative education. Retrieved online: https://www.iteea.org/File.aspx?id=86752&v=75ab076a
Yakman, G., & Lee, H. (2012). Exploring the exemplary STEAM education in the U.S. as a practical educational framework for Korea. Journal of the Korean Association For Research in Science Education, 32(6), 1072–1086.
Yeap, B. H. (2008). The Singapore mathematics curriculum and mathematical communication. Retrieved online: www.criced.tsukuba.ac.jp/math/... (YeapBanHar_Singapore.pdf).
Zambo, R., & Zambo, D. (2007). Mathematics and the learning cycle: How the brain works as it learns mathematics. Teaching Children Mathematics, 14(5), 265–270.








