10 Math Intervention Strategies for Struggling Students

Mathematics has the potential to inspire wonder and foster creativity. Deeper than counting and arithmetic, math can provide irrefutable proof of grand ideas and predict new scientific discoveries. Yet for so many students, math feels inaccessible.

As educators usher in a new generation of problem solvers, one of their biggest challenges relates to current math proficiency levels. This article provides strategies to help educators maximize and accelerate students’ growth, no matter where they are on their mathematical journeys.

What Is Math Intervention?

In broadest terms, math interventions are ways to help students who are behind in their math learning. However, for many educators, the meaning of math intervention is the support provided specifically to students who are two or more grade levels behind in a math topic.

Some schools offer dedicated classes—frequently with a smaller class size and more than one teacher—for these students who would benefit from intensive math intervention. Interventions can also be given in the course of core math instruction to individual students or small groups.

Tier 2 Intervention and Tier 3 Intensive Intervention

The strategies described in this article can be thought of as Response to Intervention (RTI) math strategies. RTI is a commonly used multi-tiered system of supports for interventions within the core classroom. In this system, students’ instruction is structured with three tiers:

• Tier 1: Students receive research-based instruction within their core classroom.
• Tier 2: Students receive targeted supplemental intervention using differentiated instruction.
• Tier 3: Students receive individualized, intensive intervention within their core classroom or in a pull-out model.

Planning Lessons for Students Who Are Struggling

The strategies in this article could theoretically be used in the course of all tiers of instruction. Here, they are discussed as ways to intervene when a student is falling behind. The supports that your students will always depend on your individual district, school, and students. Feel free to try the ideas below, adapting them to your individual needs.

Explore this list of math intervention strategies before giving a lesson, as they can be used in whole-class or small-group math instruction and guide what problems to use in the first place.

Strategy 1: Account for Student Strengths

So your student doesn’t like math class? Or maybe doesn’t seem to make any progress with the topic you’re teaching? Well, what do they like? Account for the whole student. Ask about their family, hobbies, and interests. Maybe there’s a class they love or a previous math topic that interested them. Consider creating an interest survey where students share their feelings about math, which can extend to interests outside of math, too. Look for ways to connect what your students love to the math topic that’s confounding them.

This can also be an opportunity to introduce students to new ideas and subjects that they didn’t even know would be of interest to them. If your math program includes videos or simulations, encourage your students to explore. If it doesn’t, seek out free options online. Listen to your students, and figure out what engages them so you can tap into what they care about.

This isn’t a simple task for you, the teacher! You may need to research details about your students’ interests and work out the mathematical connections. It may help to browse our full library of free resources, including math activities that relate to fashion, sports, business, and art, to name a few.

Strategy 2: Use Schema-Based Instruction

Word problems can leave students across all grade levels wondering where to even start. The combination of parsing English and manipulating mathematical concepts can be daunting, especially for multilingual learners. One evidence-based strategy is to create a schema, or an underlying blueprint or structure that you can introduce students to and continually revisit when working through word problems. For example, consider the following word problems:

• Alice has 81 fish that she has to place evenly into 9 buckets. How many fish are in each bucket?
• Rosario wants to hang 25 artworks into 5 galleries so that every gallery has the same number of artworks. How many artworks go in each gallery?
• A pet shelter has 18 cat treats that it wants to give out evenly to the 6 cats in the shelter. How many treats will each cat get?

All of these problems can be described using a schema that describes the general concept of division:

• Total ÷ Groups = Number per group

Once you have a schema, you can refer back to it to help students illustrate problems and adapt new word problems to the same schema. It may help to draw the schemas, create posters for the ones that appear most frequently, or—if your students are ready—see if they can define their own schemas.

Strategy 3: Peer Tutoring

Want to know one of the best ways to learn math? Teach it. Seriously. Ask math teachers of all stripes, and they can attest that having to explain an idea to others makes them learn it more soundly than they ever thought possible. This can be a scary strategy to employ when the students don’t seem to have mastered a concept yet themselves, but plenty of learning can happen through the teaching process. Having students talk to each other about math fosters rich math conversations. It also helps students identify classmates who are strong counterparts in terms of helping them when they're stuck.

Pair students up and have them teach a concept to each other. Be sure to give them teaching tools even if they’re struggling themselves. For example, you could provide (or have students create!) cards with numbers, equations, images, or vocabulary terms. The “tutor” can select the cards, and the “tutee” can sort them and form rules that describe all of the cards in each group. The tutor is there to check the work and correct misunderstandings. After 5–10 minutes, have students reverse roles: the tutor becomes the tutee. Not only does this strategy improve math understanding for both students; it can bolster confidence and attitudes about math, too.

If your students could use some practice with division, try out the card sort activity below, which comes from Math 180, our math intervention solution for students in Grades 5 and up.

Strategy 4: Practice Fact Retrieval

Part of what stops a lot of students from progressing in math is getting stuck on math facts. After all, if you can’t fluently add and multiply, how can you be expected to solve larger problems that rely on those facts?

Modern evidence suggests that math facts should not be the focus of lessons and are improved in the course general math practice. That said, evidence also shows that setting aside some time for practicing math facts—around 10 minutes per day—can reap large dividends in terms of confidence in math class and growth in math competency beyond fact fluency. There are endless ways to practice math facts with students, including video games, board and card games, and the strategy that follows: Cover-Copy-Compare.

Fact fluency can also be thought about in the context of problem solving. When solving math problems, don't quickly correct an arithmetic error and move on. Instead, spend time on it and have students discuss their thought processes. Consider employing number talks: 5- to 15-minute conversations around mental computation problems, which are great at getting students to work naturally on their fact fluency and speed of recall.

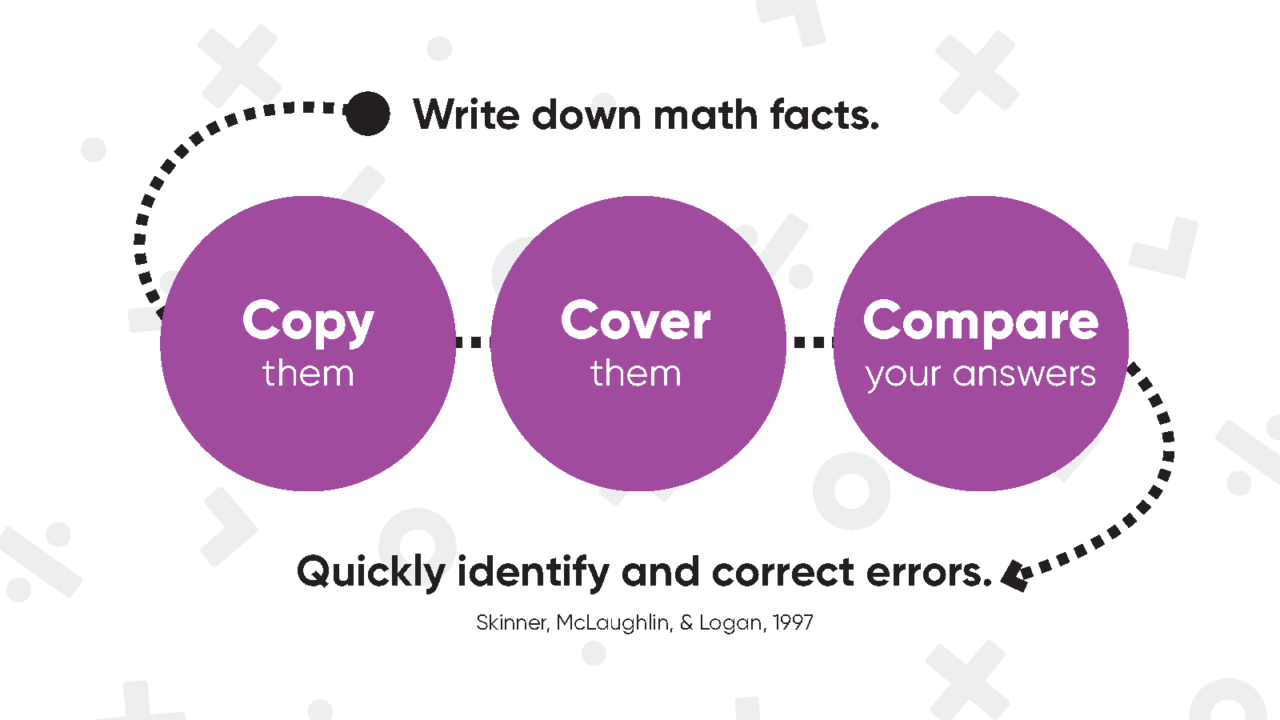
Strategy 5: Cover-Copy-Compare

This is an intervention that offers a specific evidence-based activity to practice fact retrieval. In preparation, create a worksheet with around 10 math facts. Have the list of sums or products (for example) lined up along one side of the paper. Let students study the facts and, when they’re ready, cover the lined-up numbers and try to recreate the list. When they’re done, compare the list they generated to the original list.

Mark the facts correct or incorrect. If any are incorrect, repeat the procedure of covering, copying, and comparing until all the facts are solved correctly. This task helps create a definable and manageable goal for students—get all of the facts correct—no matter their current math abilities. You can differentiate the task by having students answer orally instead, which has the added benefit of being quicker. This routine improves math accuracy both across general education and special education, and can apply to math ideas beyond just math facts. For example, this strategy could be used to build fluency with inequality symbols.

Strategies to Use While Teaching

Try this list of math interventions while giving a lesson, as they can be tools to help individual students—or groups of students!—who seem stuck on a problem.

Strategy 6: Employ Metacognitive Strategies

Research has shown that if you can get students to think critically about their own mathematical thinking, there is an opportunity to grow. On the surface, the problem may seem to be an understanding of math concepts, but the deeper problem may in fact be the students’ mindsets.

Encourage students to tell their own math stories. What was math like in their household and in previous classes? Intentionally draw your students’ attentions not just to what the math concepts are, but how they feel about them. Have students pause to reflect on how they feel and what thoughts are crossing their minds. Are they thinking thoughts like “I’ll never get this” or “There’s nothing I can do about it?” Present ways to combat this thinking, such as taking a break, asking for help, or brainstorming a new strategy to try.

Strategy 7: Use a Number Line

One of the beauties of mathematics is how many ways the same idea can be modeled. The concept of 3 × 4, for example, can be illustrated as repeated addition, an area model, or a number line, to name a few. All of these models are important, and some will of course stick better with one student over another. 

However, the number line is of special long-term importance. It is among the most versatile models in all of mathematics. The number line is a way to model magnitude, arithmetic, and—if you make two number lines orthogonal to one another—even the area model itself! According to a report from the Institute of Education Sciences, “when a teacher consistently uses number lines during intervention, students gradually develop the ability to visualize a number line.” They can then call on that specific mathematical tool in situations like solving a problem or evaluating reasonableness.
 

Moreover, the number line is a mental model we’re truly born with. Although there is debate about whether it’s intrinsically left-to-right or how linear vs. logarithmic it is, the scientific consensus seems to be that humans are born with an innate ability to represent numbers along a number line. Thus, no matter where students are in their math achievement, they have this tool they can be guided to use.

Strategy 8: Verbalize Thought Processes

Research shows that the most successful math interventions are explicit and systematic. One way to do that is to verbalize thought processes. In other words, as students think about how to solve a problem, probe them to say what they are thinking aloud. It is important here to listen patiently and without judgment even if their mathematical language is inexact or their reasoning is imperfect. When you hear the full process, it can help you identify specifically how to intervene. Perhaps they understand a larger idea but get stuck on the arithmetic. Or perhaps they understand what a problem is asking but shut down as soon as they encounter a fraction.

It can work the other way, too. As you solve a problem, verbalize your thought process. Let students see the steps you take to work through a problem and model precise mathematical language and reasoning.

Strategy 9: Fast Draw

Fast Draw is a learning strategy devised by Cecil D. Mercer and Susan P. Miller around 30 years ago to help students with learning disabilities in solving math word problems. The letters of Fast Draw are a mnemonic for the steps:

• Find what you are solving for: Look for the question mark and underline what you are trying to solve for.
• Ask yourself what information is given: Read the whole problem and look for what information is already provided.
• Set up the equation: Write the equation with numbers and symbols in the correct order.
• Tie down the equation: Say out loud what the operation is and what it means. If you can, solve the problem. It may help to draw pictures.
• Discover the sign. Find the sign and say it out loud.
• Read the problem. Say the problem out loud.
• Answer the problem, or draw.
• Write the answer to the problem.

Here’s a resource from James Madison University that provides details on each step, along with examples. Students struggling in mathematics often become passive when faced with word problems, and Fast Draw offers a concrete strategy that can help them become active and work through word problems on their own. The strategy not only helps bolster math achievement, but math attitudes, too, especially for students with learning disabilities.

Strategy 10: Use Multiple Representations

Multiple representations are important well beyond math intervention. They help students perceive math concepts in different ways and form important generalizations. However, they can serve a more targeted purpose for a student who needs targeted help. Showing math representations in different ways gives students a variety of mental models to consider, making comprehension more likely. In other words, it helps students “see” the math, even when one representation confuses them. The card sort activity from Strategy 3: Peer Tutoring is one way you can prepare specific multiple representations for students to compare.

Even concepts that seem simple to you can be complex to your students. Since everybody without visual impairments is a visual learner, lean into multiple visual representations to demystify ideas. But be intentional in which representations you show. If the representations are hard to interpret or come across as disconnected, you risk confusing students more!

***

Looking to unlock mathematical learning in the students who need it most? Explore our math intervention programs for students in Grades 3–12.

This blog, originally published in 2020, has been updated for 2024.