
Educators have been increasingly interested in the transition from arithmetic to algebra, accompanied by an interest in algebraic thinking in the elementary grades. While some people define algebra as “generalized arithmetic,” it in fact is a very different way of thinking than merely numerical or computational arithmetic. It is a system of logical reasoning. It is a representational system involving manipulation of symbols, not numbers, and a subject of study in mathematics. It is about structures and relationships.
For example, if a student is given the equation 2x + 5 = 15, a good arithmetic student can solve this mentally, not by finding an equivalent equation that isolates the unknown. Perhaps a better strategy would be to ask the student to write the equation that represents the question, “5 more than double a number is 15, what is the number?” This question focuses on the representation of a relationship using a variable, and not on the particular numbers.
The transition from arithmetic to algebra is challenging, but if students are introduced to algebra concepts throughout the elementary grades, that transition is made easier. This can be done first by making sure students have sufficient understanding and fluency with critical topics such as whole number computation, fractions, ratios, and proportionality, and second by explicitly teaching critical algebraic ideas and reasoning. Some of the topics explicitly taught include generalizations, recognizing structures, properties, equivalence, use of variables, and creating visual models to solve algebraic problems.
The study of generalizations
Mathematics is the study of generalizations—of finding a relationship that applies across a set of objects. It requires looking across objects and cases for similarities, differences, and definable commonalities. It is leading to abstraction, to a stripping of context.
For example, students in the beginning of third grade are asked to consider the effects of adding an even number to an even number, an odd number to an odd number, and an even number to an odd number. After trying several versions of each of these, students are asked if that relationship is always true. Students often will provide additional examples as proof that an even sum results when the two addends are even or when both are odd. The teacher is then suggested to ask why this relationship holds, which forces students to move away from additional examples and instead focus on the meaning of even and odd numbers. What do all even numbers have in common and what do all odd numbers have in common?
The use of manipulatives encourages students to see even numbers as pairs and odd numbers as pairs plus 1. In later grades this will become 2n and 2n + 1. Students will discuss if 0 is an even number, then later in the year, students will look at the multiplication table in the same way and make generalizations about the products of even and odd numbers. They will answer the questions of whether there are more even or odd products on the table and why.
Introducing structures and properties
When the multiplication facts are taught as related facts and students learn facts by using these relationships, they are introduced to structures and properties.
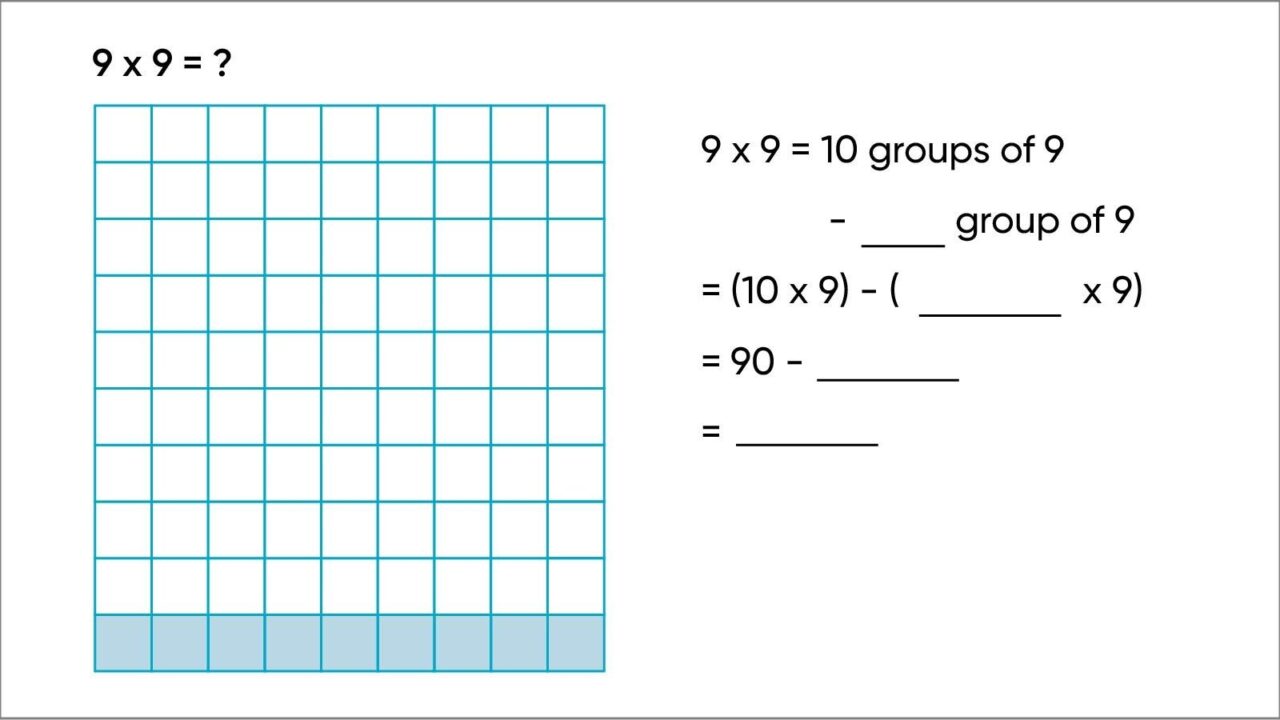
For instance, students are encouraged to use an area model to learn the facts for 9 using the related facts for 10. To learn 9 x 9, students already know 10 groups of 9 equals 90, so just one less group of 9 would equal 81. Similarly, students learn that 9 times any number is one less group than 10 times a number. This will be used later for problems like 9 x 15 is (10 x 15) – 15. Eventually this will become 9n = 10n – n. Some students may prefer to break down 9 x 9 to be (5 x 9) + (4 x 9), which introduces the distributive property. So much mental arithmetic depends on this distributive property and is needed in the expansion and factoring of variable expressions. The focus is not on the technical names of properties but on an understanding that structures like the associative, commutative, and distributive properties enable both number and symbol manipulation.
Functional thinking
Students are introduced to functional thinking from the beginning of kindergarten, where they learn to count, to the end of eighth grade, where they learn what a function is and multiple ways of representing a function. Even by fourth grade, students use functional thinking to solve problems by considering linear growing patterns, as in this example:
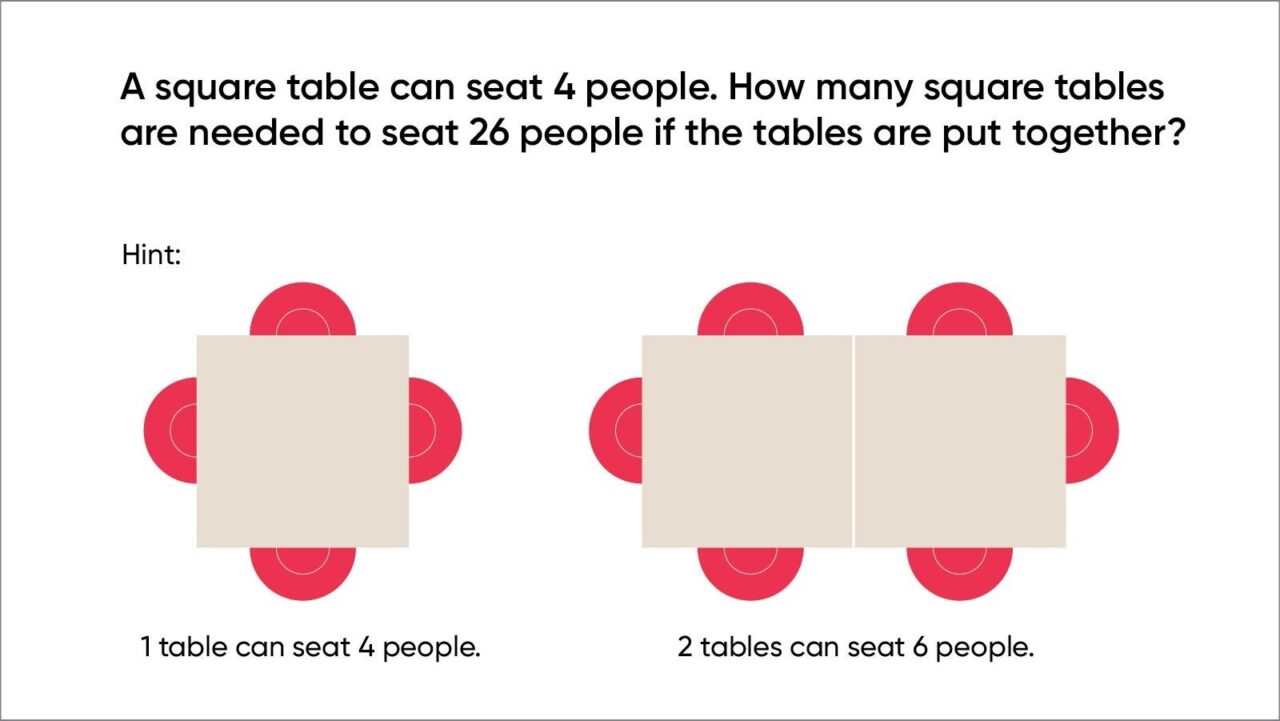
Students use many strategies to solve this problem. They look for a pattern 4, 6, 8, 10, and so on. They recognize that each table adds two people. They count the people on each side of the table. They subtract 2 from the 26 for the end people and then divide 24 into 2. They use a variety of strategies that all lead to generalizations for any number of people.
The concept of variables
The concept of a variable is also challenging but introduced early in first grade. Part of the reason the concept of a variable is challenging is that it is used in a variety of related but different ways. In some cases, a variable represents a set of numbers, as in the expression 2n. In other cases, the variable represents a single unknown, as in 2x = 10. In another case, variables are used to describe a relationship or function, as in y = 2x + 5. Finally, while we tell students that a variable may be any symbol, when it is used in a formula, such as A = ½ bh, the specific letters do matter and stand for parts of the triangle.
Students should be provided opportunities to use variables in all these contexts. In first grade students are presented with the problem below. Students are asked to consider all the numbers that would satisfy the condition, and the blank lines are used to represent all those numbers.
Karina sees some monkeys in a zoo.
The zookeeper tells her there are fewer than 15 monkeys. Katrina writes the addition sentence to show the number of monkeys.
10 + _______ = _______
Talk about some of the likely answers with your partner.
By fifth grade, after the introduction of visual models (called bar models) to represent variables in second and third grade, students are asked to solve more complex algebraic problems using bar models. Such a problem is shown below.
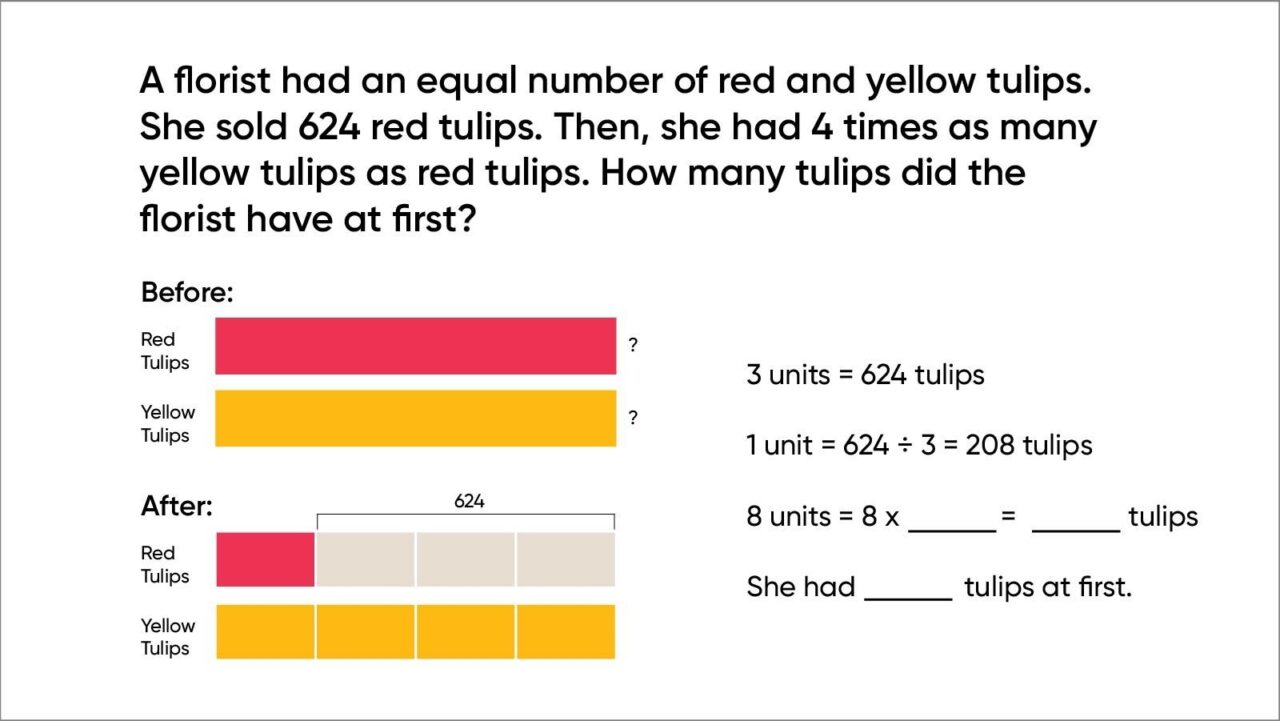
The concept of a variable and relationships between quantities are represented with bar models that can easily become symbolic variables. In sixth grade, students solve positive variable equations. In seventh grade, students solve problems with rational coefficients and variables on both sides. In eighth grade, students solve systems of linear equations. Even when solving sophisticated problems, reference is made to the bar models, which now include the use of x and y to represent quantities.
If math is taught with understanding and not as a set of procedures, students become used to looking for generalizations and structures. Students who think of mathematics this way are more able to understand the structures that are introduced in algebra. Teachers are encouraged to ask questions such as: “Is this always true? How do you know? How can you represent this relationship?” Questions like this help students move away from specific arithmetic examples and into generalization and common structures.
***
Learn more about how Math in Focus®: Singapore Math® by Marshall Cavendish® supports the transition from arithmetic to algebra in the elementary grades
The blog post originated from a white paper by Andy Clark.
Originally published in 2019, this blog post has been updated in 2025.
Be the first to read the latest from Shaped.












