
I present to you a magic trick that can be done fully online:
- Think of a number. Any number at all.
- Add 4.
- Multiply by 3.
- Subtract 9.
- Divide by 3.
- Now subtract your original number.
Let me guess . . . did you end up with 1?!
There is a whole world of “tricks” like this where you can perform a series of calculations that results in not just a predictable number, but even meaningful numbers like your age or birthday. These kinds of tricks are fun for the classroom, yet they have a nefarious side to them—they make math seem like “magic” or “tricks.” Follow these mysterious steps and then bam! The answer appears!
Mathematics is anything but a series of magic tricks, however. These kinds of diversions can engage and empower students. Yet it is important to peel back the curtain and show the math behind why a trick works. These kinds of tricks can be deconstructed, and there are math lessons that can be taught using that deconstruction. Consider how the previous magic trick can be turned into basic algebra:
- Think of a number. Call it x.
- Add 4: x + 4
- Multiply by 3: 3(x + 4) = 3x + 12
- Subtract 9: 3x + 12 – 9 = 3x + 3
- Divide by 3: (3x + 3)/3 = x + 1
The History of Magic Squares
Magic squares date back thousands of years and have enchanted artists, writers, and mathematicians ever since. According to A History of Mathematics, the first written record of a magic square appeared in China, around 2000 BC.
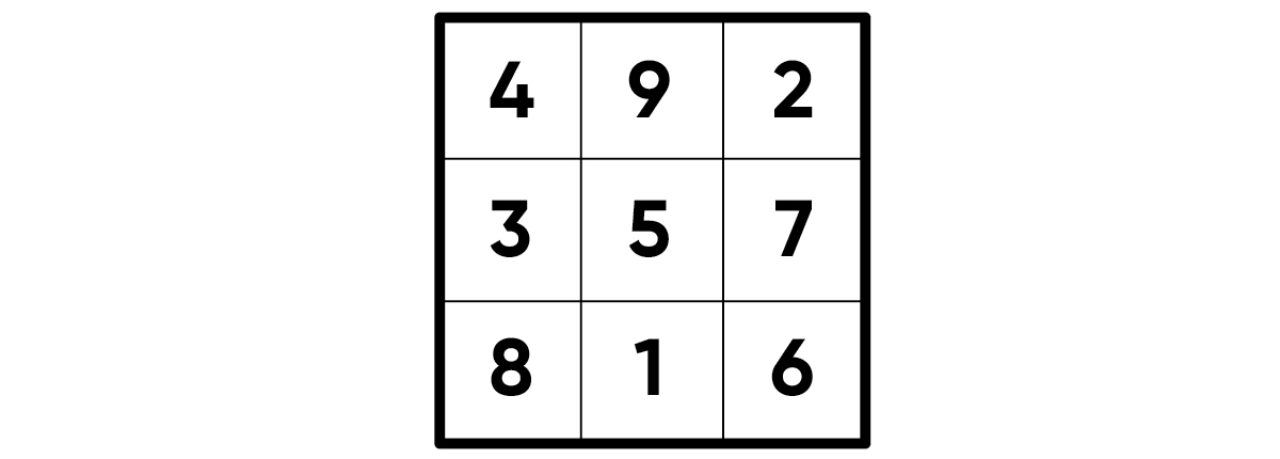
This square is called “magic” because if you add up the numbers in any row, column, or diagonal, it always equals the same number (as if by magic). In this case, the magic sum is 15. Because this square has exactly every number from 1 to 9, students may recognize this magic square as a possible part of a Sudoku grid—a popular number-based puzzle that people play. Restricting the allowable magic square numbers to be the digits 1 through 9 also creates an opportunity to analyze how to construct a magic square. In the 2021 book Activity Gems for the Grades 9–12 Classroom, authors Peggy House, Sharon Stenglein, and Roger P. Day provide great questions that have students thinking like mathematicians:
- Why must the magic sum be 15?
- Why can none of the numbers 6, 7, 8, or 9 occupy the center square?
- What number must occupy the center square?
It would be several thousand years before evidence of magic squares appeared in the West. There is a print from the early 1500s in the collection of the Metropolitan Museum of Art by German artist Albrecht Dürer, which shows a 4 × 4 magic square in the top-right corner.
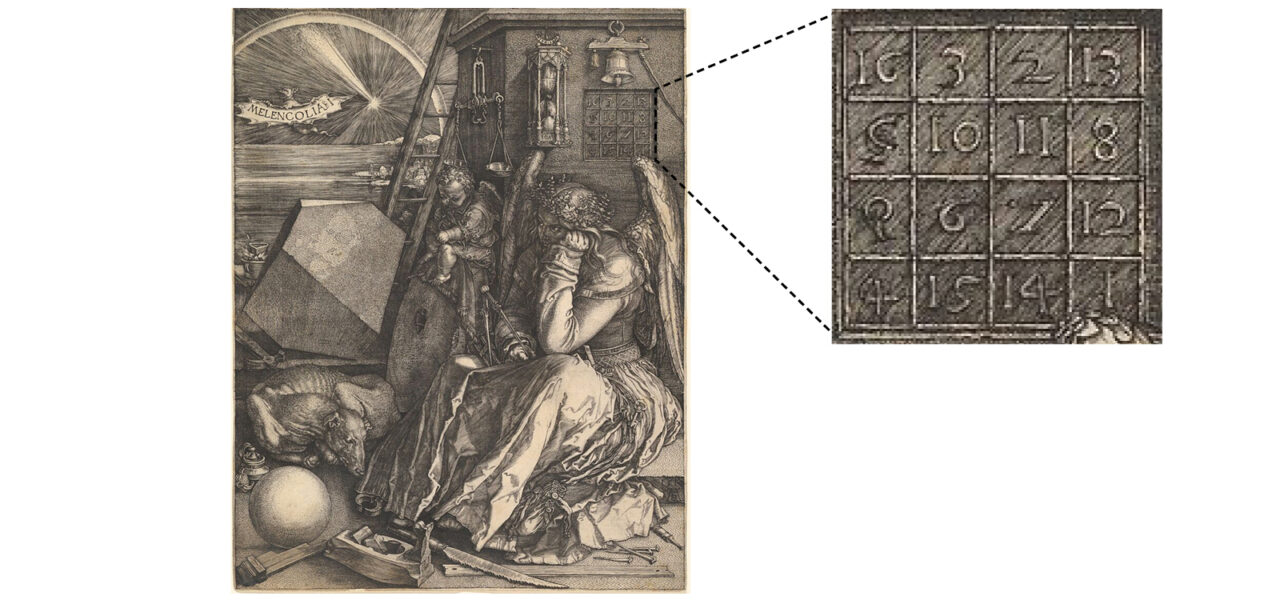
The Met Museum’s website explains how the magic square is there to show how mathematics “underlies artistic creation.” Dürer was especially mathematically precise when creating art, not only in his lines and angles but also, in this case, down to showing a magic square that works!
Why Do Magic Squares Work?
The mathematics of magic squares is in fact quite complicated. It is not as straightforward as the algebraic “magic trick” that introduced this article, where introducing an x suffices to explain how it works. For those looking to dive in, I direct you to W. S. Andrews’ 1908 compendium Magic Squares and Cubes—hundreds of pages on the characteristics, history, and construction methods for magic squares, along with mindboggling extensions like magic cubes, circles, spheres, stars, and octahedroids.
The theory of magic squares might be too advanced for most students, but that doesn’t mean these mathematical curiosities still can’t be explored and discussed, even by very young children. Most students should be able to answer basic questions about what they notice and wonder about the simpler 3 × 3 magic square shown earlier:
- How many rows and columns does the magic square have?
- What is the sum of each row, column, and diagonal?
- Why are there the same number of rows as columns?
Depending on the students’ readiness, there are many ways to extend the discussion:
- If you multiply or divide each number by the same amount, will it continue to be a magic square?
- If you add or subtract each number by the same amount, will it continue to be a magic square?
- If you rotate the square 90°, 180°, or 270°, will it continue to be a magic square?
- Why does it get much harder to construct a magic square every time you add a row and column?
This sort of wide-ranging entry into the math is a feature of HMH Into Math, our K–8 core math curriculum. When a math task is thought-provoking and high-quality, students can enter the task in different ways using what they know and can do so far.
Mathematics and Magic
There is a long history of math being used in the construction of magic tricks, from small card tricks to making an elephant disappear. “Many mathematicians are amateur magicians,” writes researcher Fernando Blasco. “Mathematical ideas can be applied to different types of magic tricks.” That is, the attention to precision, logic, and problem-solving that lead one to excel in mathematics can also lead to designing great illusions.
In the earliest days of stage magic—during the mid-1800s—magicians were able to make people appear and disappear as “ghosts” through the clever use of mirrors and glass plates. These had to be positioned at specific angles inside a theater, and the magician was responsible for calculating these angles. Throughout magic’s history, math came into play when planning many different types of illusions:
- For large-scale illusions (such as making an elephant disappear, a trick explored in great detail in Jim Steinmeyer’s 2003 book Hiding the Elephant), the magician must account for “sight lines,” to ensure that no audience members will see how the trick is done, regardless of their viewing angle.
- Card tricks that involve revealing cards at the right time can involve stacking cards in a precise, mathematically-derived order, either before the trick or during the trick.
- Large-scale apparatuses for hiding people and objects are often constructed with careful measurements so that they look too small to have anything inside.
- Tricks involving ropes and rings often work because of their topology, a branch of mathematics that can help to derive how to arrange objects so that they appear tangled together but in reality are not.
There is also a class of stage magic known as mentalism, where a magician appears to read people’s minds, but is in fact taking advantage of natural laws, human behaviors, and information that was obtained in secret. The “Guess My Number” math trick, along with the trick that began this article, could both be considered mentalism tricks that take advantage of the “natural laws” of mathematics.
Mathematician Martin Gardner was especially famous for inventing magic tricks that followed mathematical principles. His 1956 classic book Mathematics Magic and Mystery details many ways that math can be used to perform magic tricks. Here’s a completely different type of “magic square” that Gardner provides as a trick that makes it seem as though the magician is performing a complicated addition problem rapidly and without a calculator (p. 48):
The magician turns away while a spectator selects a month of the calendar, then draws on the page a square of such size and in such position that includes nine dates. The magician is told the smallest of these numbers. After a moment’s calculation [the magician] announces the sum of the nine numbers.
Method: Eight is added to the number and the result multiplied by nine.
The book provides a source for this and similar tricks, though for middle schoolers, trying to understand why this trick works is a great introduction to algebraic concepts. (If the first calendar date is expressed as x, how could the remaining eight dates be expressed in terms of x? What is the sum of all nine expressions?)
Math and “Tricks”
Of course math class is not (usually) the place to carefully stack a deck of playing cards or construct a box to hide inside. When the word “trick” is used in a math classroom, it’s usually in reference to a clever way of solving a specific problem or class of problems. Math education expert Dr. Jane Wilburne presents a famous historical example:
I love the story of Carl Friedrich Gauss—who, as an elementary student in the late 1700s, amazed his teacher with how quickly he found the sum of the integers from 1 to 100 to be 5,050. Gauss recognized he had fifty pairs of numbers when he added the first and last number in the series, the second and second-last number in the series, and so on.
In other words, Gauss realized that the sum of all numbers from 1 to 100 can be arranged into symmetric pairs of numbers where each pair adds up to exactly 101:
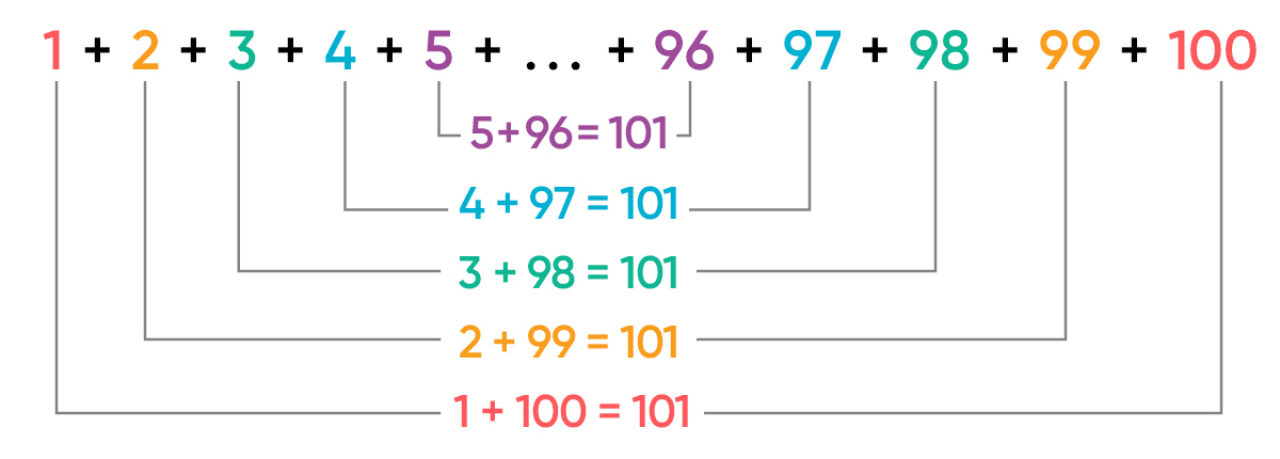
Because there will be exactly 50 of these pairs (half of 100), Gauss used this “trick” to calculate that the sum of all integers from 1 to 100 equals 101 × 50, or 5050.
This is what a “trick” looks like in math. A “trick” offers a deceptively easy solution to an otherwise difficult problem. It often showcases an innovative or unexpected approach. You or your students may be familiar with “tricks” like this one to find the product of 9 and a number between 1 and 10:
- Hold out both hands so that 10 fingers are visible from left to right.
- Curl the finger representing the number between 1 and 10. For example, if multiplying 9 by 4, curl the fourth finger.
- Count the number of fingers on either side. For example, if you curl your fourth finger, there are 3 fingers to the left and 6 fingers to the right—and 9 × 4 = 36.
“Tricks” are one-offs that can solve individual problems and make for rich discussion, but they are not a substitute for building conceptual understanding in math. Even common strategies like using the standard algorithm to multiply and divide are in a way just “tricks.” They work in many cases and can be a helpful tool for students. However, it is not obvious why they work. Teachers need to explain the why, and students can quickly run into cases where these tricks fail.
Ultimately, one goal of a math teacher should be to make math engaging for students, but think twice the next time you refer to any mathematical process as a “trick.” There is plenty of math to be found in constructing magic tricks, and there are plenty of tricks that students learn as shortcuts. But there are no tricks to what makes math work!
***
HMH offers a host of core and supplementary math solutions for grades Pre-K–12. Our curriculum, instruction, assessment, and professional development are all aligned to foster students’ academic growth and build teachers’ effectiveness. Learn more here.
Get our FREE guide "Optimizing the Math Classroom: 6 Best Practices."













