Folding Shape Activities to Practice Geometry

What Is Symmetry?

In first and second grade we introduce the concept of geometry by teaching students the main attributes of shapes. We begin by teaching the common shapes, like circles, squares, triangles, and rectangles. A lesson may include identifying how many sides and angles a shape has, the length of its sides, and similarities and differences between shapes. An important attribute to identify is whether or not the shape is symmetrical.

One way to teach the concept of symmetry to young students is by showing them that when folding paper shapes, each “equal side” of the shape should be the same, or mirror itself. When a shape has at least one line of symmetry, it is considered a symmetrical shape.

• Key Standard: Identify a shape that is symmetrical or asymmetrical

Folding Common Paper Shapes Activity

For this folding shapes activity, students will need cut-out paper shapes and a highlighter. We recommend having a variety of common shapes pre-cut and ready for your students to fold. The pre-cut shapes will give the students a better opportunity to identify symmetry. Feel free to use our free cut-outs of common shapes.

To start this activity, you will want to teach your students the key vocabulary term: line(s) of symmetry. A way to learn what a line of symmetry is by folding paper shapes and then examining the result. Have you and your students grab the paper square and ask them to identify which shape it is. Then ask if they think a square can be folded in half so that one half of the fold fits exactly on top of the other half of the fold.

Demonstrate, and walk students through how to fold a shape in half, explaining that when folding shapes in half, the edges and corners need to be lined up and touching. After that first fold, have students open their shape back up and explain to the students that the folded line is known as a line of symmetry. Prompt students to look for different ways they could fold the same square to create another line of symmetry. Guide students in discovering that a square has four different lines of symmetry.

Ways to support students:

• Have students use a highlighter to highlight the folded line each time they identify it as a line of symmetry. When students independently explore their paper shapes, they may create a lot of folded lines that are not lines of symmetry. By having the students mark them, they will easily be able to look back at that shape and count how many lines of symmetry they identified.
• To differentiate instruction for some students, provide a “dot” at the center of the shape to help them identify where to fold to find half. The students will be able to reference whether the dot was located on the folded line.

The circle is a special shape that has an infinite number of lines of symmetry. Before your students begin folding their circles, ask them to guess how many lines of symmetry a circle has. Record some of the answers you receive on the board so you can compare what they guessed and what they discovered after they folded their shapes. Allow your students the time to explore their circle and see how many lines of symmetry they can create. After everyone has completed folding their circle, look back and have a discussion about their guesses and discoveries. Point out no matter which way you fold a circle in half it will always be considered a line of symmetry.

For students who are ready, this can lead to a discussion on what infinity means. Mathematically, there are infinitely many lines of symmetry. But in reality, it is impossible to fold a circle an infinite number of times. Can students think of other examples of infinity? For example, how large numbers can get or how many points are on a line.

Progressing Through Common Shapes

One progression through the shapes could be to start with the easiest shapes to identify lines of symmetry for, and to end with the more challenging shapes. An example of this progression could be square, diamond, rectangle, trapezoid, circle, and ending with different types of triangles (equilateral, right, and isosceles).

Through the progression, students may recognize that shapes with equal side lengths will often have more lines of symmetry than shapes with diverse side lengths. For instance, a square has four sides of equal length and four lines of symmetry.

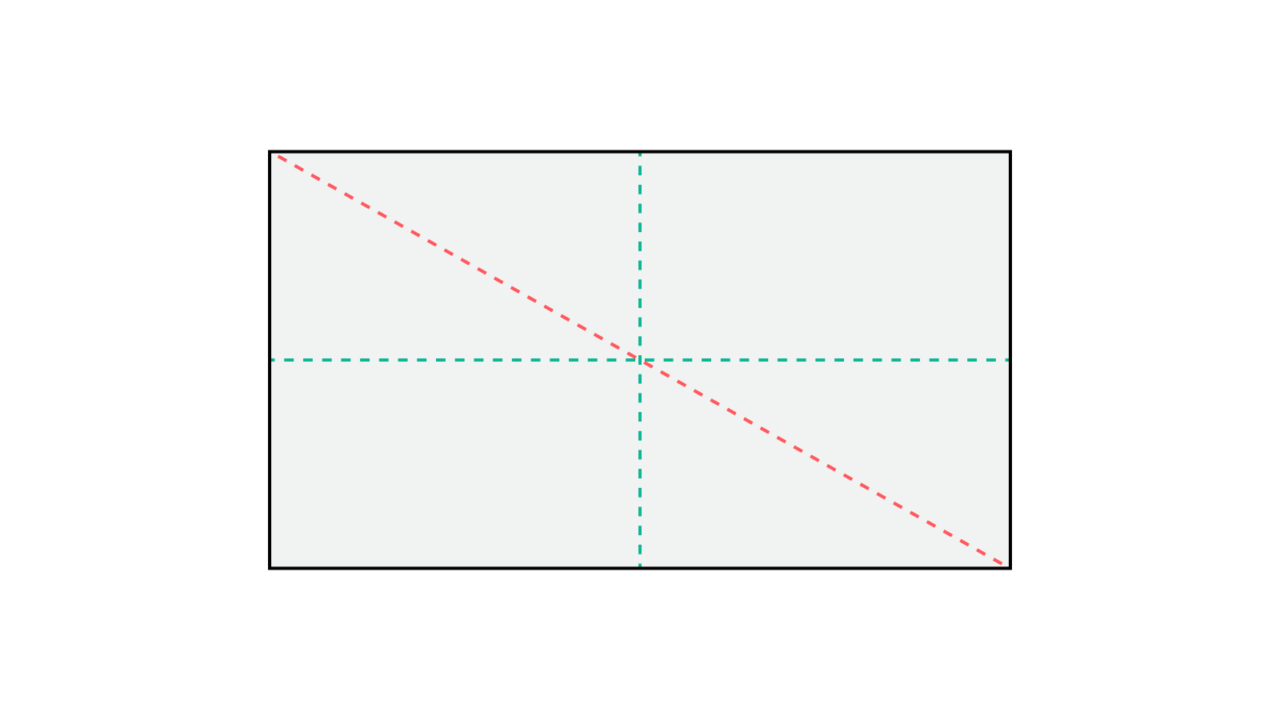
The rectangle is a great example to introduce students to shapes that can be folded in half and have folds that are not lines of symmetry as well as folds that are. The rectangle has exactly two lines of symmetry. Ask all the students to grab their paper rectangle and fold it vertically. Remind students that they need to fold their shapes exactly in half, meaning that the edges and corners of the paper need to be lined up and touching.

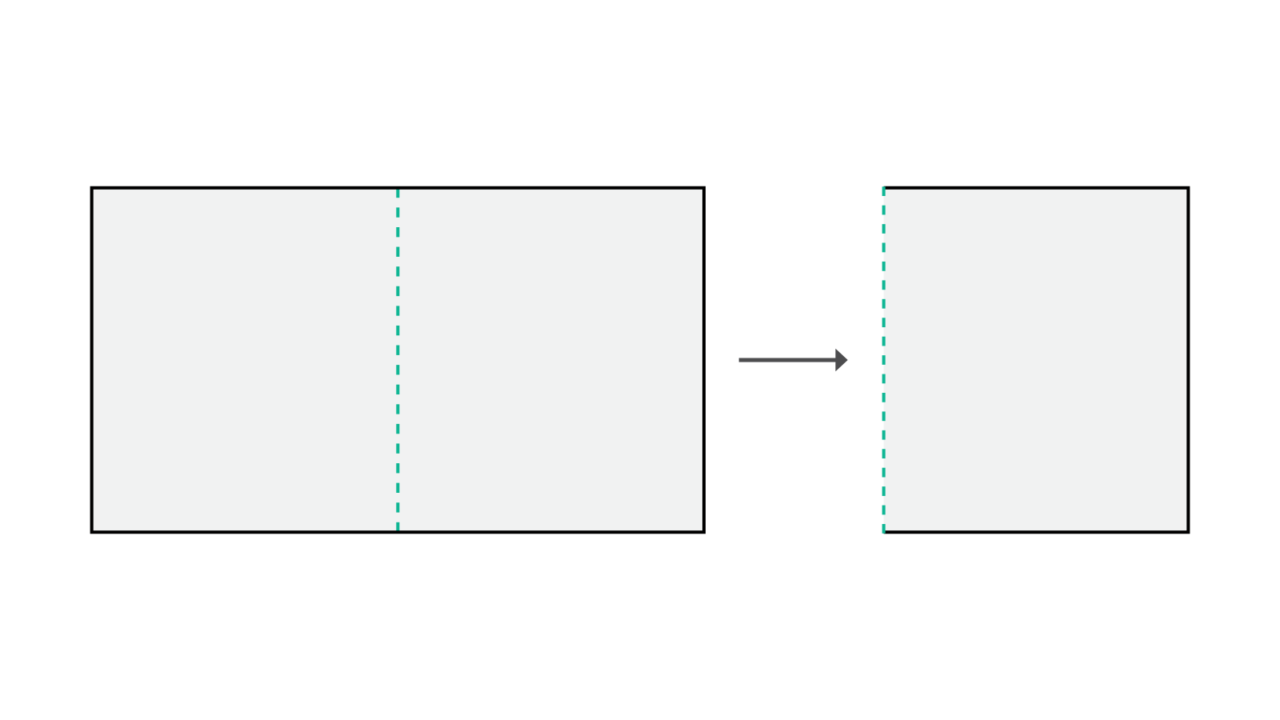
Shapes can have more than one line of symmetry. After students have folded the rectangle once, have them independently explore the shape by unfolding it then trying to fold it in different directions to identify other lines of symmetry. Students can highlight their lines of symmetry with a highlighter to not confuse them from other folding lines that might not have worked out to be symmetrical. Take a moment with your students to discuss what led them to create folded lines that weren’t lines of symmetry. Avoid telling students they were right or wrong, instead seeking to elicit their thinking about lines and shapes and compare their thinking with their peers. Lastly, ask the students to unfold their shape and count how many lines of symmetry they found.

Take a moment to wrap up this lesson by reviewing some key points:

• What is a line of symmetry, and how do we find it?
• What are some shapes that always have lines of symmetry when folded in half?
• What are some shapes that don’t have lines of symmetry when folded in half?
• Why is a circle special?

Folding Uncommon Paper Shapes Activity

In this activity students will work with symmetrical and non-symmetrical shapes. Provide students with pre-cut uncommon shapes and a highlighter. Cut-outs for some uncommon shapes are available below.

Similar to the Folding Common Paper Shapes Activity, you will work through different shapes and identify different lines of symmetry.

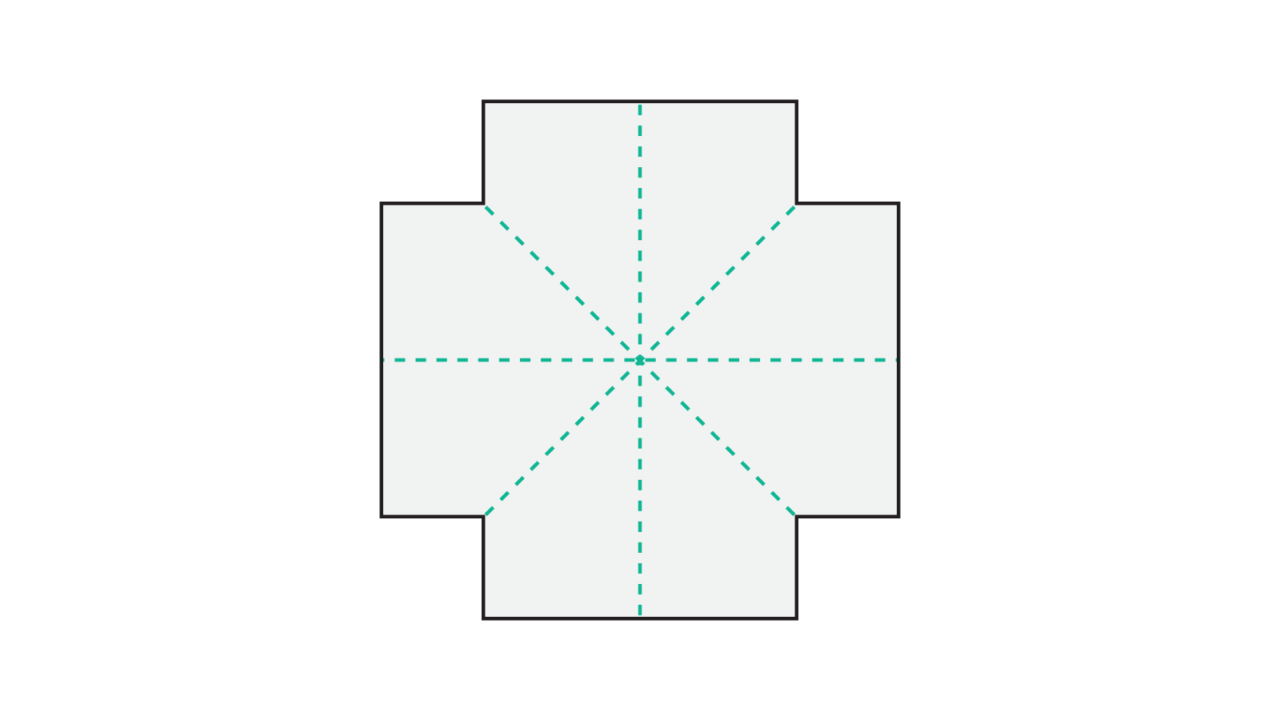
To start this activity, you will want to review what symmetry is and how to find out if a shape has lines of symmetry. If the folded shapes have even one line of symmetry, that makes the shape symmetrical. Have students grab the shape that resembles a plus sign, then allow them time to fold it and discover if the shape has any lines of symmetry.

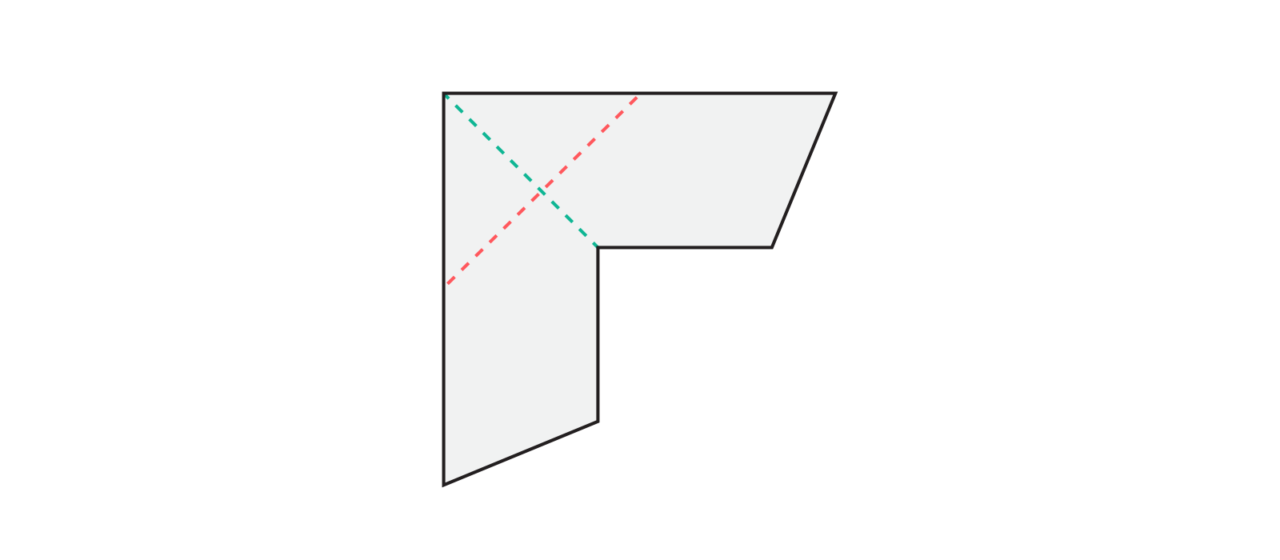
The next progression of this activity is to introduce the students to an uncommon shape that has only one line of symmetry. Have students grab the paper shape that resembles an arrow and give them time to explore this shape to see if they can identify any lines of symmetry.

The last part of this activity is better for students who are ready for more advanced geometry ideas. We find that students enjoy the opportunity to create their own shapes. Have your students cut out any shape they want from a piece of paper. Encourage students to make shapes that are funny and unique. This is a great time for them to be creative. If it helps, you can demonstrate how to make random cuts that will result in an odd-looking shape. Although a goal of this part of the activity is to encourage student exploration, if you think there won’t be enough time, you can provide them with a pre-cut uncommon shape.

Once all students have created their folded shape, ask them if they can find any lines of symmetry. The goal of this exercise is for the students to create shapes that won’t contain any lines of symmetry. If any students create a shape that is actually symmetrical, explore how that happened and discuss the differences between shapes with and without symmetry.

Take a moment to wrap up this lesson by reviewing some key points:

• Can uncommon shapes be symmetrical?
• What is the folded line called when we can fold a shape perfectly in half?

Are there shapes that are not symmetrical and how would you be able to tell?

Extension Activity

For an extension activity or an exit ticket, assemble a grid of 10–15 different shapes taken from the real world, for example stop signs, leaves and flowers, and outlines for tools or toys. Students can identify lines of symmetry on each shape. Students can then highlight as many lines of symmetry that they can find in the symmetrical shapes, while leaving the asymmetrical shapes blank.

Additional Symmetry Activities

An engaging way to have students continue to identify lines of symmetry is to have them finish drawing the other half of a pre-drawn image. This activity will familiarize students with finding the halfway point in a figure as well as getting them to realize that symmetrical shapes should look the exact same on each side of the line of symmetry.

Find a few images that you believe your students would enjoy completing. The easiest way to create this activity is to print the full image, then fold it in half and make copies of one of the folded sides. Keep in mind the complexity of the image; we suggest using images that aren’t super detailed.

Once the activity is over, don‘t forget to point out symmetry in the world around you throughout the year! One of the joys of mathematics is learning about an idea and then seeing all the ways that it can describe phenomena, objects, and ideas. Students might start to see their classrooms, living environments, and natural world just a little bit differently now.

The views expressed in this article are those of the authors and do not necessarily represent those of HMH.

***

Grow student confidence in mathematics with HMH Into Math, our core math solution for Grades K–8.