Response to Intervention: An Alignment Guide to Math 180

Houghton Mifflin Harcourt^® (HMH^®) has prepared this Alignment Guide to assist local education agencies (LEAs) and schools that are currently implementing or are considering adopting a Response to Intervention (RTI) approach. This guide provides key background information on current educational policy related to RTI and describes how Math 180 can complement and strengthen the implementation of RTI to raise student achievement as well as identify students with learning disabilities. This Alignment Guide provides the following information:

• RTI Overview
• Math Intervention and the Role of Math 180
• Math 180 Overview
• Alignment of Math 180 to RTI Core Components

Math 180 is designed to address the needs of striving students in Grades 5 and up and their teachers. To meet the needs of middle-school students who are one or more years behind in math, Math 180 focuses on deep understanding and mastery of the essential skills and concepts necessary to unlock algebra and advanced mathematics. The Math 180 scope and sequence is built around a focused and coherent curriculum that enables students to progress successfully toward grade-level curriculum.

Math 180 is based on three main principles: (a) instruction focused on content essential for being prepared for algebra; (b) teacher supports for instruction and progress monitoring; and (c) development of a growth mindset in students.

Math 180 delivers this support through the following:

• A total of 18 instructional blocks divided into six manageable Block Series focused on numerical reasoning and pre-algebra. Topics focus on: multiplication, division, fractions, decimals, rate, ratio, percent, functions, equations, and linear relationships.
• A blended learning model integrating whole-class and small-group instruction, individualized learning software, and anytime/anywhere personalized computer math games
• Support for teachers by providing step-by-step lessons that are scaffolded and paced especially for students who have struggled with math
• Emphasis on visual models, multiple strategies, student interaction, and meaningful practice so all students have opportunities to master concepts and skills
• Embedded formative and summative assessments that can be used for progress monitoring so teachers can measure achievement and differentiate math instruction according to individual needs
• Professional learning resources and materials that support instruction to meet all students’ diverse needs

This Alignment Guide addresses how Math 180 supports the implementation of RTI. For questions regarding funding sources for Response to Intervention services, please consult your local Account Executive or state educational agency (SEA).

This Alignment Guide is informed by the Every Student Succeeds Act (ESSA), IDEA 2004 Regulations, the National Association of State Directors of Special Education (NASDSE) 2005 Report, guidelines provided from the Vaughn Gross Center for Reading and Language Arts at the University of Texas at Austin, and consultation with Dr. Joe Witt, author of the iSTEEP model on the core principles and practical implementation of RTI in schools.

The reauthorization of the Individuals with Disabilities Education Act (IDEA 2004) changed the way students are evaluated for special services by encouraging schools to use research-based interventions to address the diverse needs of students through early intervention as well as identify and work with struggling learners at risk for school failure. The ESSA has provided states greater flexibility in determining the specific practices and service delivery models, including multi-tiered systems of supports such as RTI, to ensure access to comprehensive learning supports.

Response to Intervention is not a particular program, curriculum, or model. Rather, it is a framework for allocating instructional services that are aligned to students’ individual needs to maximize student academic achievement. It aims to prevent unnecessary assignments to special education through the provision of tiers of intervention and continuous progress monitoring.

The RTI framework requires schools to:

• Implement a universal screening process to identify striving learners
• Provide an effective program for all students and intervention for those who fall behind
• Rigorously implement services through tiers of increasingly targeted and intensive, research-based intervention services matched to students’ needs
• Measure and continually monitor students’ learning rate and performance over specific periods of time
• Adjust the intensity and nature of the intervention services in light of student response (or non-response) to services provided
• Use resulting data to drive instructional decision making

The purpose of RTI is to:

• Integrate student assessment and instructional intervention within a multi-tiered prevention system to maximize student achievement.
• Intervene early and monitor at-risk students in need of individualized instruction and specialized services
• Identify students with learning and other disabilities (in accordance with state law)
• Better integrate services between general and special education populations

There are many variations of RTI models highlighted in the literature and utilized in practice. However, many share the following core components that allow them to be effective agents of change.

RTI uses a multi-tiered model of service delivery to promote efficient response to students’ needs. Each tier provides increasingly intensive support structures to ensure that students succeed.

Tier 1: Core Instructional Interventions

• General curricula for all students
• Proactive interventions based on instructional variables within whole-group instruction

Tier 2: Targeted Group Interventions

• Supplemental instruction for students who are not successful in Tier 1
• Targeted interventions oriented toward small-group instruction
• Explicit instruction, rapid response

Tier 3: Intensive, Individual Interventions

• Individualized instruction for students who are not successful in Tier 2
• Intensive interventions oriented toward individual students
• Diagnostic assessments to determine student need
• Higher intensity, longer duration

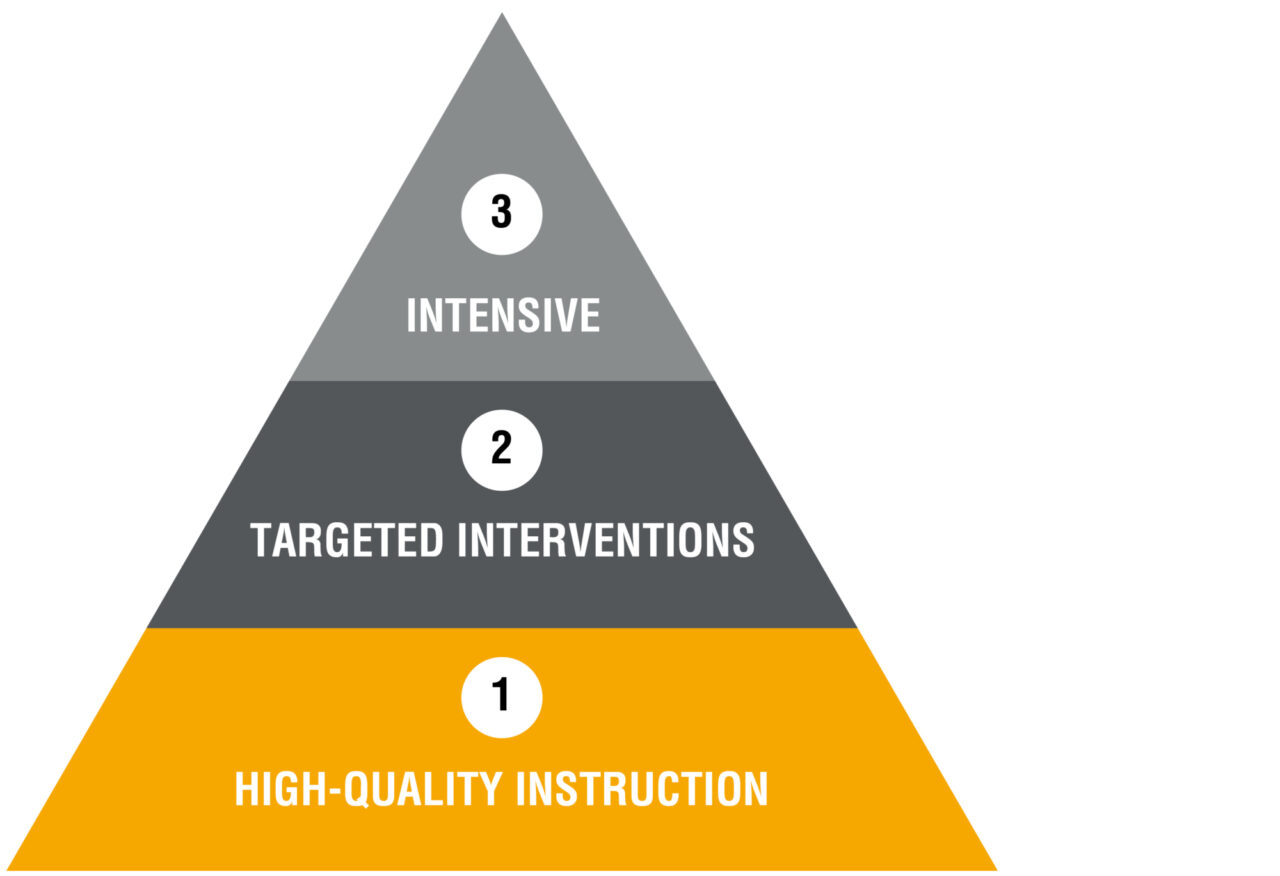
Three tiers of intervention allow schools to offer increasingly intensive interventions to those students who are not making adequate progress in the core curriculum (Tier 1). Increasing intensity can be achieved by: (a) using more teacher-centered, explicit instruction; (b) employing more frequent intervention sessions; (c) extending the duration of the intervention; (d) working within smaller, more homogenous grouping; or (e) relying on specialists or instructors with greater experience to implement components of the intervention (Fuchs & Fuchs, 2006). Student responses are measured to determine whether students have made adequate progress and no longer need the intervention, continue to need some intervention, or need more intensive intervention.

Screening measures should be brief, reliable, and valid, and they should help identify those students who require more intense interventions. Screenings are performed at the beginning, middle, and end of the academic year. More information (e.g., through additional assessment or diagnostic interviews) is gathered from children who perform below the benchmarks associated with the screener to determine root causes for learning difficulties.

IDEA 2004 and ESSA (and formerly NCLB) require that interventions be evidence-based. ESSA sets forth four levels of evidence: strong evidence, moderate evidence, promising evidence, and demonstrates a rationale. Interventions applied under Title I, Section 1003 (School Improvement) are required to have strong, moderate, or promising evidence to support them.

Student progress is assessed on an ongoing basis and is used to inform planning and instruction. The selected method of assessment is anchored in mathematical content and is, as well, brief, targeted to assess specific skills, and easily administered. The goal of progress monitoring is to quantify student rate of improvement (i.e., comparing a student’s expected and actual rate of learning) and instructional effectiveness.

In all tiers of intervention, data from screening and progress monitoring measures should be used to make instructional decisions for individual students. Data on an individual allow adjustments to the nature and intensity of interventions. Schools can also aggregate data to compare and contrast the curriculum, instructional effectiveness, and different components of the intervention for various subgroups of students within the school. It is also an alternative method for identifying students with learning disabilities after students have demonstrated nonresponsiveness to evidence-based instruction and intervention.

Use supplemental instructional materials, where appropriate, to strengthen the efficacy of the comprehensive core curriculum and support student learning.

Instructional strategies should be included to address the specific needs of multilingual learners.

A high-quality professional services plan should be included to support teachers who are implementing interventions within the RTI framework. The plan should allow for coaching and other opportunities.

Components of RTI funded by IDEA may be coordinated with activities funded by, and carried out under, the Elementary and Secondary Education Act (ESEA).

According to the 2019 National Assessment of Education Progress (NAEP) Mathematics test, 59 percent of America’s fourth graders are not proficient in mathematics. The NAEP data also reveal that 66 percent of eighth graders are not proficient in mathematics. These numbers clearly pointed to the challenges confronting mathematics education. However, since NAEP testing was last conducted, the nation was confronted with a new set of challenges from the COVID-19 pandemic that had significant impacts on all corners of the educational landscape. Although evidence is still emerging on the final impacts of the pandemic on student progress, early results point to significant declines in student achievement. These declines have disproportionally affected already at risk groups of students, such as American Indian and Alaska Native (AIAN), Black, and Latinx students, as well as students in high-poverty schools (Lewis, Kuhfeld, Ruzek and McEachin, 2021). Unless these declines are addressed, the impact of what is sometimes referred to as “unfinished learning” can have significant negative consequences for those affected for years into the future (Dorn, Hancock, Sarakatsannis and Viruleg, 2021).

The National Mathematics Advisory Panel’s (NMAP, 2008) Final Report establishes fluency with whole numbers, fluency with fractions, and some aspects of geometry and measurement as critical foundations for algebra. With over two-thirds of eighth-grade students in the United States not proficient in these areas, they are not prepared for success in algebra. Unfortunately, lack of preparation for success in algebra can have dire consequences. Research conducted by University of California, Santa Barbara’s California Dropout Research Project (Silver, Saunders, & Zarate, 2008) showed that 65 percent of students who failed to pass Algebra I by the end of ninth grade failed to graduate on time.

Also, one percent of school-age children experience a math disability not associated with any other learning disability, and two to seven percent experience serious math deficits. Students with mild disabilities do not perform as well as their peers without disabilities on basic operations, and this discrepancy in performance increases with age (Cawley, Parmar, Yan, & Miller, 1996). In addition, students with math disabilities may respond with lower self-esteem, avoidance behaviors, and decreased effort. Learning math is also a challenge for many English learners, as the content presents its own unique academic vocabulary and is often presented abstractly.

The Every Student Succeeds Act requires that all students in America be taught to high academic standards that will prepare them to succeed in college and careers, and the goals of the National Council of Teachers of Mathematics (NCTM, 2000) aspire for all students to become mathematical problem solvers, learn to communicate and reason mathematically, use representations to model problem situations, and make connections among mathematical ideas. In addition, the National Mathematics Advisory Panel recommends that math curricula for elementary and middle school be a coherent progression of key topics with an emphasis on proficiency with key topics. For many students, especially those who struggle, meeting those goals presents a challenge when they receive only the typical 50 minutes per day dedicated to math instruction. Moreover, many students require instruction that is specifically designed to meet them at their level and to focus on the most critical foundational mathematical concepts.

Math 180 addresses these learning challenges facing American students. The program’s instructional design applies what is known about reaching a wide variety of students who struggle with math to achieve proficiency with the essential concepts and skills that provide a foundation for success in algebra.

Math 180 is designed to address the needs of striving students in Grades 5 and up and their teachers, equally—building students’ confidence with mathematics and accelerating their progress to algebra. Math 180 picks up the progression to algebra at whole number multiplication and builds a coherent narrative of understanding through fractions and decimals, proportional reasoning, and functional thinking. Conceptual models and procedural strategies build on one another, opening up and facilitating new learning. Instruction is organized into Six Block Series, each with three blocks of instruction and three topics. Math 180 uses a blended learning model in which students rotate between teacher-facilitated instruction and personalized software that adapts to their needs.

Math 180 gives students who have fallen behind the chance to catch up and keep up. Math 180 students develop the skills they need to compute with accuracy and efficiency, the numerical and proportional reasoning they need to reason through mathematical situations, and the ability to apply their skills and reasoning to solve problems.

Each learning experience in Math 180 encourages students to link concepts and skills to their corresponding mathematical representations and language. The range of assessments to measure growth and formative and summative tests to monitor progress gives teachers various ways to measure achievement and adjust instruction according to individuals’ needs. In addition, suggestions for differentiating instruction, strategies for supporting English learners, a series of professional services options, and various materials offer multiple means for addressing every student’s needs.

The following information outlines how Math 180 addresses the Core Components of a Response to Intervention Model.

Math 180 is designed to be used flexibly by educators to address specifically Tier 2 or Tier 3.

Tier 2 is characterized by targeted group interventions for students who are considered to be at risk: students instructed in a regular core program (Tier 1) whose conceptual knowledge and habits of mind are fragile and need the additional support offered in Tier 2. Students in Tier 2 are collectively give scaffolded instruction, which is paced specifically to meet their needs. Unlike most textbooks, which typically cover a broad range of topics, Math 180 focuses on the concepts and skills essential to long-term student success in algebra and advanced mathematics. Math 180’s guided instruction anticipates common errors or misconceptions, and the blended instructional model helps all students move through phases with increasing independence. In addition, the formative and summative assessments reveal what students know and whether they have mastered the set of objectives taught. After every topic, students’ performance is used to track their growth so teachers can make data-based decisions to adjust the intervention to meet student needs.

Tier 3 students are typically individual students who demonstrate minimal or no response to the intervention services provided in Tier 2. The intervention is further intensified and individually customized to meet the needs of students. Which components of Math 180 are intensified are based on the embedded progress monitoring, and this is followed by suggestions for differentiating instruction.

Math 180 supports those students who struggle with math and those who require differentiated instruction by providing the following:

Six Different Block Series

Math 180 consists of a total of 18 instructional blocks divided into six manageable Block Series that cover multiplication, division, fractions, decimals, rate, ratio, percent, functions, equations, and linear relationships. These topics were selected to provide striving students the concepts and skills they need to be prepared for algebra.

Meaningful Practice

The lessons in Math 180 intertwine conceptual understanding with procedural skill so students learn the mathematical steps in conjunction with the reasons behind them. Targeted and deliberate practice builds fluency with those procedures. After students watch a video that introduces the new concepts in a problem-solving context, the concept is then broken down from concrete to representational to abstract, through the use of interactive mTools and the introduction of mathematical language and symbols. Every lesson in Math 180 models reasoning and provides rigorous scaffolded practice; as students advance, they build conceptual fluency and model reasoning in order to prepare for high-order performance tasks.

Suggestions for Differentiation

Technology-based learning provides assessment and instruction data for every student through ongoing formative assessments and progress monitoring, and Math 180 translates these data into meaningful data snapshots and interactive analytics to target instruction and group students according to their needs. Math 180 also provides teachers with supplemental resources for differentiated instruction and problem solving.

/blog/wha...Math 180 incorporates Growth Measure at the beginning, middle, and end of the school year to provide educators and students a more complete view of the student’s academic growth and performance. The ability to administer Growth Measure in under 45 minutes and to use the data from it to group students, drive instructional next steps, and support RTI and MTSS initiatives makes it a powerful tool for educators.

Growth Measure provides educators with actionable data about their students’ skills including an HMH Scaled Score, performance categories (overall and by domains), Student Growth Index (SGI), Grade Level Equivalence (GLE), and Quantile® Interval. Additionally, Math 180 incorporates student progress monitoring throughout the curriculum. At the end of each topic within each instructional block, student progress is measured and students are then grouped, based on their performance.

Math 180 is designed to engage and empower learning experiences, support teachers in maximizing instructional effectiveness, and give administrators the tools to ensure high-quality implementation. The following proven instructional strategies are drawn from a foundation of research.

Focus
Math 180 maintains a tight focus on the concepts, strategies, and content knowledge that constitute the progression to algebra. Covering fewer topics in more depth is particularly important for students who struggle with mathematics (Gersten et al., 2009). Math 180 addresses students’ incomplete number and operation knowledge (ACT, 2010), deficits in rational number understanding (Kloosterman, 2010; NCTM, 2007; Siegler et al., 2010), and limited ability to solve contextually based problems (Hoffer, Venkataraman, Hedberg, & Shagle, 2007) that can hinder students’ transition from arithmetic to algebra (NRC, 2001).

Coherence
Math 180 delivers a coherent curriculum in which concepts build on one another in a logical progression. Students’ mathematical knowledge builds as progressions between grades and between topics (Core Standards, 2010). Instructional tasks that develop mathematical understanding build on students’ previous learning and interests and cause students to struggle in meaningful ways to develop important mathematical ideas (Hiebert et al., 1997). Coherence, building on foundational skills year after year, is one of the most important characteristics defining quality content standards (Schmidt, Houang, & Cogan, 2002).

Rigor
Math 180 delivers on three aspects of rigor: conceptual understanding, procedural skills and fluency, and applications. Math 180 lessons intertwine conceptual understanding with procedural skill so that students learn the mathematical steps in conjunction with the reasons behind them. Students’ content knowledge improves as they solve problems with authentic contexts (Gersten et al., 2008), develop understanding of problem structures, and gain access to flexible solution strategies (Jitendra & Star, 2011).

Communication and Standards for Mathematical Practice
To foster a communicative classroom culture, Math 180 provides explicit instruction in mathematical vocabulary and language support. Constructive classroom discourse allows students to integrate mathematical tools and language with everyday tools and language (Cobb, Jaworski, & Presmeg, 1996), focusing on the meaning being developed while the communication occurs (Moschkovich, 2012). The Standards for Mathematical Practice are varieties of expertise employed by mathematically proficient students. Math 180 emphasizes these standards in all aspects of the program. For students to develop mathematical proficiency, the Standards for Mathematical Practice must become an integrated part of their learning (Confrey & Krupa, 2010). The standards support students in developing conceptual understanding, procedural fluency, strategic competence, and adaptive reasoning (NRC, 2001).

High-Leverage Teaching Practices
Math 180 supports teachers in implementing high-leverage teaching practices through point-of-use professional learning. Teachers learn how, why, and when to differentiate, foster meaningful class discussions, and elicit and respond to student reasoning. The Math 180 approach is aligned with research that shows that professional services should develop teachers’ mathematical content knowledge, understanding about how students think and learn about mathematics, sense of self as a teacher of mathematics (Sowder, 2007), and curricular knowledge (Ball, 1988; Remillard & Bryans, 2004).

Data-Powered Differentiation
Data-powered differentiation enhances student learning by supporting teachers in providing instruction that accommodates the differences in learning needs among individual children (Sousa & Tomlinson, 2011). Providing teachers with specific information about how each student is performing consistently enhances students’ mathematics achievement (NMAP, 2008; Baker. Gersten, & Lee, 2002). Several studies show that all children, including those who have been traditionally underserved, can learn mathematics when they have access to high-quality instructional programs that support their learning (Griffin, Case, & Siegler, 1994; Knapp et al., 1995; Silver & Stein, 1996).

Multilingual Learner Support
Math 180 instruction begins with progressive language development goals; all mathematical terms are provided in Spanish and English, and on the student software many mathematical instructions are translated and all written instructions are read aloud. Explicit vocabulary instruction is important because students may have existing notions about words such as product, factor, times, and sum that do not align with the mathematical meanings of such words (Allen, 1988; Ball et al., 2005; Doabler, Nelson and Clarke, 2016; Garrison & Mora, 1999). When multilingual learners are presented with mathematics instruction and techniques that make concepts and operations comprehensible and are presented with additional language and academic support that meets their needs, they are able to be successful (Garrison & Mora, 1999).

Special Needs Student Support
Math 180 provides students with special needs a wide variety of supports that may be unavailable in traditional classrooms. Universal Design for Learning principles are integrated into Math 180 at all levels to facilitate productive learning opportunities for all students. Instructional tools and methods that have been proven effective for students with learning disabilities, such as immediate corrective feedback at each step of a problem (Vaughn & Roberts, 2007), visual models to promote deep understanding (NMAP, 2008), systematic and explicit instruction of concepts (NCTM, 2007), cooperative and peer-mediated learning techniques (Fuchs et al., 1997), and differentiated lesson design, all contribute to a classroom culture that supports all learners.

Growth Mindset
Math 180 builds student competence and confidence aligned with research on mindset. Students with a growth mindset believe their intelligence and abilities can be developed and improved over time through effort and dedication. Students who understand that sustained effort and deliberate practice over time are crucial to achieving mastery and expertise show more resilience and effectiveness in their pursuit of mastery (Dweck, 2000; Ericsson, 2006). In contrast, striving students are more likely to have a negative, fixed mindset toward their own mathematical abilities (Pashler et al., 2007). Middle school students who were taught mathematics study skills, and that the brain is like a muscle that grows with effort, displayed a sharp increase in math achievement in relation to students who were taught only mathematics study skills (Blackwell, Trzesniewski, & Dweck, 2007).

For additional supporting literature on the development and efficacy of Math 180, please consult the Math 180 Research Foundation Paper. /research/math-180-research-foundations

Continuous monitoring and progress monitoring are necessary to determine whether the interventions being implemented are working and to support teachers in differentiating instruction. Math 180 provides a suite of progress monitoring tools and integrates tools to support teachers in using student progress data to adjust instruction accordingly.

• Progress monitoring occurs through the interim assessments built into Math 180. At the end of each topic, students’ abilities to apply learned concepts and skills are measured. At the end of each instructional block, students’ application of mathematical strategies in real-life contexts, application of learned skills, acquisition of concepts and reasoning, and depth of mathematical knowledge are measured. Additionally, Math 180 offers Growth Measure three times per year, providing teachers data on students’ reasoning and problem-solving strategy progress. Teachers then use the results to select and implement the suggestions for differentiation included in the program and make decisions about targeting instruction according to each student’s needs.
• Daily opportunities for formative assessment are built into Math 180 so teachers can make sense of what students do and have yet to understand. Progress monitoring occurs daily as student complete tasks in the Learn Zone, Brain Arcade, and mSpace.

Math 180 includes a variety of assessments and extensive data analysis tools to help teachers monitor students’ progress and target instruction to meet all their students’ diverse needs.

Math 180 provides comprehensive class- and student-level data to monitor students’ progress and performance in the program. Teachers use Growth Measure tools to track student progress toward grade-level standards and algebra readiness, to help group students for differentiated instruction, and to monitor ongoing overall growth in math understanding.

Upon completion of each block, students complete the Explore Zone and mSpace performance tasks, which provide the teacher with documentation for mathematical growth in skill and understanding demonstrated by each student.

Supplemental instructional materials are available for use, where appropriate, to strengthen the efficacy of a comprehensive core curriculum and support student learning. Math 180 provides materials that support both teachers and students and could be used to complement any core program.

Teacher Guides give teachers the information necessary for teaching the lessons, including step-by-step teaching instructions, guidance for monitoring student progress, and specifics about how to use the other materials provided in the program.

• Math 180 on Ed provides online access to myriad professional resources related to the program, including videos, reproducibles, and standards alignments.
• Math 180’s Resources for Differentiated Instruction and Problem Solving pdf provides teachers mathematical and pedagogical support, including additional lessons, for differentiating instruction to meet student needs.
• Brain Arcade computer-based games allow students to choose among 11 math games that improve procedural fluency and strategic thinking, as well as choose the topic and the difficulty with which they are willing to play. Games are proven to be risk-free environments that destigmatize failure, demarcate progress, and reward persistence, and the Brain Arcade games encourage students to pursue their personal mathematical goals with a sense of independence and agency.

Math 180 is designed to grant maximum access and success for English learners, with an emphasis on developing language for math, the incorporation of visual representations and directions, and consistency across all instructional routines.

• Math 180’s classroom routines prepare all students for individual success and ensure they are prepared to complete their work independently. Routines are well established so multilingual learners can focus on the content and not the process of the assignment.
• Numerous structured opportunities for students to engage in meaningful conversations about math are embedded throughout the program to support intentional vocabulary and language development, while increasing access to content. Working in small groups allows multilingual learners to speak in their home language in order to understand the task at hand before articulating their solution with the larger group.
• Interactive visual mathematical models support all students and are especially supportive of those who are multilingual learners.
• Math vocabulary is taught explicitly. Vocabulary is introduced through a consistent routine of “hear it, see it, say it, and define it”. Every lesson highlights key math and academic vocabulary used. Spanish translations of each key word or phrase are provided.
• Sentence frames provide access to common sentence structures for students who who are learning English, allowing them to engage in mathematical conversations.

Math 180 offers a variety of professional services solutions. A Math 180 subscription includes:

Embedded Professional Service

• Collaborative implementation planning and goal-setting
• Getting Started and Follow-Up training sessions
• Real-world classroom resources and best practices for teachers via Teacher’s Corner^®
• Family Resources for family and caregivers with easy-to-understand resources, available in English and Spanish
• Leader Learning with resources from Teacher’s Corner accessed directly from the administrator dashboard

Coaching Membership

Districts can partner with an HMH Instructional Coach to meet their specific needs. Teachers benefit from collaborative sessions that facilitate instruction within Math 180—delivered live, online, and in person using HMH Coaching Studio. Coaching provides an opportunity to focus on standards-aligned instruction and practice through lesson modeling, lesson planning, and data analysis.

Live, Online Courses

HMH’s Live Online Courses allow teachers to create a customized implementation plan. Here is a sample agenda from the course Engaging in Math Workshop Structures and Tasks:

• Introduction to Math Workshop
• Establish and Build Your Math Workshop Community
• Start and Finish Strong: Number Sense Routines and Student Self Reflection
• Math Workshop: Deep Dive into Learning Stations
• Math Workshop: Deep Dive into Guided Math
• Math Workshop: Deep Dive into Math Tasks and Focus Lesson

Leadership Advisory Services

HMH provides school- and district-wide wide transformative advisory services for leaders. Advisory Services Include:

• 30 hours of live, online leadership advisement
• Partnership to plan, implement, and refine action agendas
• Customized leader learning pathway
• Support for social and emotional learning initiatives

Math 180 can be purchased and implemented, using a variety of sources including state funds, funds from local districts, or donations from private foundations. For questions regarding funding sources for Response to Intervention services, please consult your local Account Executive or state educational agency (SEA).

Math 180 strongly supports an effective implementation of RTI in schools. Math 180 is a research-based math intervention program that proactively improves middle school students’ access to the core curriculum by differentiating and targeting intervention for groups of students who need additional support (Tier 2), or providing assessments and targeted interventions for individual students who have not yet acquired a foundational understanding of key topics in number and operations (Tier 3).

Incorporating research-based instructional strategies to specifically meet the needs of students who struggle with mathematics, Math 180 helps students gain the necessary conceptual understanding of the topics critical for being prepared for success in algebra. Moreover, there are assessments and suggestions for differentiation embedded in the program that guide the teacher as to when a student may need additional support in order to succeed. Ongoing progress monitoring, professional service resources, and supplementary materials further assist practitioners to use the program effectively to meet the goals of RTI.

ACT. (2010). A first look at the Common Core and college and career readiness. Iowa City, IA: Author.

Allen, F. B. (1988). Language and the learning of mathematics. A speech delivered at the National Council of Teachers of Mathematics Annual Meeting, Chicago, IL.

Baker, S., Gersten, R., & Lee, D. S. (2002). A synthesis of empirical research on teaching mathematics to low-achieving students. The Elementary School Journal, 103(1), 51–73.

Ball, D. L. (1988). Unlearning to teach mathematics. For the Learning of Mathematics, 8(1), 40–48.

Ball, D. L., Mundy, J. F., Kilpatrick, J., Milgram, R.J., Schmid, W., & Schaar, R. (2005). Reaching for common ground in K–12 mathematics education. Notice of the AMS, 52(9), 1055–1058.

Blackwell, L. S., Trzeniewski, K. H., & Dweck, C. S. (2007). Theories of intelligence predict achievement across an adolescent transition: A longitudinal study and an intervention. Child Development, 78(1), 246–263.

Cawley, J., Parmar, R., Yan, W. F., & Miller, J. (1996). Arithmetic computation performance of students with learning disabilities: Implications for curriculum. Learning Disabilities: Research and Practice, 13(2), 68–74.

Cobb, P., Jaworski, B., & Presmeg, N. (1996). Emergent and sociocultural views of mathematical activity. In L. P. Steffe, P. Nesher, P. Cobb, G. A. Goldin, & B. Greer (Eds.), Theories of mathematical learning (pp. 3–19). Mahwah, NJ: Lawrence Erlbaum.

Common Core State Standards Initiative. (2010). Common Core State Standards initiative for mathematics. Washington, DC: National Governors Association Center for Best Practices and the Council of Chief State School Officers.

Confrey, J. & Krupa, E. (Eds.). (2010). Summary report of a Center for the Study of Mathematics curriculum conference: Curriculum design, development, and implementation in an era of Common Core State Standards. Retrieved from http://mathcurriculumcenter.or...

Doabler, C., Nelson, J., & Clarke, B. (2016). Adapting Evidence-Based Practices to Meet the Needs of English Learners With Mathematics Difficulties. Teaching Exceptional Children, 48(6), 301–310.

Dorn, E., Hancock, B., Sarakatsannis, J., & Viruleg, E. (2021). COVID-19 and education: The lingering effects of unfinished learning. McKinsey & Company.

Dweck, C. S. (2000). Self-theories: Their role in motivation, personality, and development. Philadelphia, PA: Taylor & Francis.

Ericsson, K. A. (2006). The influence of experience and deliberate practice on the development of superior expert performance. In K. A. Ericsson, N. Charness, P. Feltovich, & R. R. Hoffman (Eds.), Cambridge handbook of expertise and expert performance (pp. 685–706). Cambridge, UK: Cambridge University Press.

Fuchs, L., Fuchs, D., Hamlett, C., Phillips, N., Karns, K., & Dutka, S. (1997). Enhancing students’ helping behavior during peer-mediated instruction with conceptual mathematical explanations. The Elementary School Journal, 97(3), 223–249.

Garrison, L., & Mora, J. L. (1999). Adapting mathematics instruction for English language learners: The language-concept connections. In L. Ortiz-Franco, N. G. Hernandez, & Y. De la Cruz (Eds.), Changing the faces of mathematics: Perspectives on Latinos (pp. 35–48.)

Gersten, R., Chard, D., Jayanthi, M., Baker, S., Morphy, P., & Flojo, J. (2008). Mathematics instruction for students with learning disabilities or difficulty learning mathematics: A synthesis of the intervention research. Portsmouth, NH: RMC Research Corporation, Center on Instruction.

Gersten, R., Beckmann, S., Clarke, B., Foegen, A., Marsh, L., Star, J. R., & Witzel, B. (2009). Assisting students struggling with mathematics: Response to Intervention (RtI) for elementary and middle schools (NCEE 2009–4060). Washington, DC: National Center for Education Evaluation and Regional Assistance, Institute of Education Sciences, U.S. Department of Education. Retrieved from http://ies.ed.gov/ncee/wwc/pub...

Griffin, S. A., Case, R., & Siegler, R. S. (1994). Right start: Providing the central conceptual prerequisites for first formal learning arithmetic to students at risk for school failure. In K. McGilly (Ed.), Classroom lessons: Integrating cognitive theory and classroom practice (pp. 24–29). Cambridge, MA: MIT Press.

Hiebert, J., Carpenter, T. P., Elizabeth, F., Fucson, K. C., Wearne, D., Murray, H., ... Human, P. (1997). Making sense: Teaching and learning mathematics with understanding. Portsmouth, NH: Heinemann.

Hoffer, T., Venkataraman, L., Hedberg, E. C., & Shagle, S. (2007). Final report on the national survey of algebra teachers for the National Math Panel. Chicago, IL: National Opinion Research Center at the University of Chicago.

Jitendra, A. K., & Star, J. R. (2011). Meeting the needs of students with learning disabilities in inclusive mathematics classrooms: The role of schema-based instruction on mathematical problem-solving. Theory into Practice, 50(1), 12–19.

Kame’enui, E. J., Carnine, D. W., Dixon, R. C., Simmons, D. C., & Coyne, M. D. (2002). Effective teaching strategies that accommodate diverse learners (2nd ed.). Upper Saddle River, NJ: Merrill Prentice Hall.

Kloosterman, P. (2010). Mathematics skills of 17-year-olds in the United States: 1978 to 2004. Journal for Research in Mathematics Education, 41(1), 20–51.

Knapp, M.S., Adelman, N.E., Marder, C., McCollum, H., Needles, M.C., Padilla, C. … Zucker, A. A. (1995). Teaching for meaning in high-poverty classrooms. New York: Teachers College Press

Lewis, K., Kuhfeld, M., Ruzek, E., & McEachin, A. (2021). Learning during COVID-19: Reading and math achievement in the 2020-21 school year. NWEA.

Moschkovich, J. (2012, January). Mathematics, the Common Core and language: Recommendations for mathematics instruction for ELs aligned with the Common Core. Paper presented at the Understanding Language Conference at Stanford University, Stanford, CA.

National Council of Teachers of Mathematics (2007). Principles and standards of school mathematics. Reston, VA: Author.

National Mathematics Advisory Panel (2008). Foundations for success: The final report of the National Mathematics Advisory Panel. Washington, DC: U.S. Department of Education.

Pashler, H., Bain, P., Bottge, B., Graesser, A., Koedinger, K., McDaniel, M., & Metcalfe, J. (2007). Organizing instruction and study to improve student learning (NCER 2007–2004). Washington, DC: National Center for Education Research, Institute of Education Sciences, U.S. Department of Education. Retrieved from http://ncer.ed.gov

Remillard, J. T., & Bryans, M. B. (2004). Teachers’ orientations toward mathematics curriculum materials: Implications for teacher learning. Journal for Research in Mathematics Education, 35, 352–388.

Schmidt, W., Houang, R., & Cogan, L. (2002). A coherent curriculum, American Educator, 26(2), 1–18.

Siegler, R., Carpenter, T., Fennell, F., Geary, D., Lewis, J., Okamoto, Y., … Wray, J. (2010). Developing effective fractions instruction for kindergarten through 8th grade: A practice guide (NCEE #2010-4039). Washington, DC: National Center for Education Evaluation and Regional Assistance, Institute of Education Sciences, U.S. Department of Education. Retrieved from http://ies.ed.gov/ncee/wwc/pdf...

Silver, D., Saunders, M., & Zarate, E. (2008). What factors predict high school graduation in the Los Angeles Unified School District? Santa Barbara: California Dropout Research Project, University of California, Santa Barbara.

Silver, E. A., & Stein, M. (1996). Mathematics reform and teacher development. Pittsburgh, PA: University of Pittsburgh.

Sousa, D. A., & Tomlinson, C. A. (2011). Differentiation and the brain: How neuroscience supports the learner-friendly classroom. Bloomington, IN: Solution Tree Press.

Sowder, J. (2007). The mathematical education and development of teachers. In F. Lester (Ed.), Second Handbook of Research on Mathematics Teaching and Learning (pp. 157–223). Reston, VA: National Council of Teachers of Mathematics & Charlotte, NC: Information Age Publishing.

Vaughn, S., and Roberts, G. (2007). Secondary interventions in reading: Providing additional instruction for students at risk. Teaching Exceptional Children, 39(5), 40–46.