At a glance
- Subjects: Math, Intervention Curriculum
- Report Type: Research Evidence Base
- Grade Level: Elementary
As states and local districts adopt more rigorous standards, our nation’s students must be prepared to face these greater challenges in order to keep pace. A strong foundation is essential for later success in mathematics, and adequate preparation is essential to their future success. According to the 2015 National Assessment of Education Progress (NAEP) Mathematics test, 60 percent of America's fourth graders are not proficient in mathematics. The NAEP data also reveals that 67 percent of eighth graders are not proficient in mathematics (National Center for Education Statistics, 2015). More students in the U.S. need to be proficient in mathematics in order to be successful in algebra. The National Mathematics Advisory Panel’s Final Report (2008) has established that fluency with fractions and other basic arithmetic concepts and skills are critical foundations for algebra. If students are struggling with the acquisition of these foundational skills, it is essential to provide the supports necessary for them to become proficient in these areas.
Success in the Early Stages of Instruction Will Lead to a Greater Likelihood of Success in the Future
Children struggle with mathematics for a number of reasons such as language, learning disabilities, and a simple lack of adequate prior exposure. English learners, for example, can struggle with understanding the mathematical concepts and vocabulary (Frederickson & Cline, 2002). Learning disabilities are a pervasive challenge in our nation’s classrooms. Between five to eight percent of school-aged children have some form of a learning disability which affects their ability to learn mathematics (Geary, 2004). One percent of school-aged children experience a math disability not associated with any other learning disability, and two to seven percent experience serious math deficits. Although these challenges can be significant, they can also be addressed especially if done so early with adequate supports for both teachers and students.
Another factor affecting the classroom is the adoption of more rigorous standards. The effects of increasing rigor also impact teachers who report changes in the way they deliver instruction. In addition, teachers report a greater need for support, especially those working with students who are one or more grade levels behind (Bay-Williams, Duffett & Griffith, 2016). Support can take several forms such as professional development and advances in technology and infrastructure.
Results from a recent national survey show that educators are more optimistic about using new technologies that enhance instruction and perform differentiated instruction. The survey also indicates that approximately 97 percent are using some form of digital technology in their classroom, and many have seen these benefits in the form of increasing student engagement and achievement (HMH, 2015).
The National Council of Teachers of Mathematics (NCTM®) Principles to Actions (2014) outline the importance of teaching and learning, tools and technology, coherent curriculum, assessment, and professional development as key components to creating “systematic excellence” in schools. In addition, the National Mathematics Advisory Panel recommends that math curricula for elementary and middle school be a coherent progression of key topics with an emphasis on proficiency. For many students, especially those who struggle, meeting these goals presents a challenge when they only receive a typical 50-minute daily session dedicated to math instruction. Moreover, many students require instruction that is specifically designed to target key misconceptions and to focus on the most critical foundational mathematical concepts.
This Research Foundations document describes a program that addresses many of these challenges and is based on decades of research used to inform its development. The document will outline and connect the eight guiding principles of Do The Math with supported research. Examples from the program will be used to demonstrate how these guiding principles impact the way students learn mathematics. Finally, a set of studies pointing to the program’s efficacy in improving student academic outcomes are summarized.
Since its inception almost 10 years ago, Do The Math has fostered student engagement in math and provided support for teachers in thousands of classrooms across the United States.
A Long History of Turning Research into Practice
Do The Math was initially published in 2008. The program is based on nearly 50 years of research and experience by Marilyn Burns working with teachers and students in the classroom. Marilyn Burns, along with a team of Math Solutions® instructors with extensive classroom teaching experience, created the lessons in Do The Math. They discussed, wrote, debated, tested, rewrote, and refined the lessons to ensure that the content, pacing, and scaffolding were on target to meet the needs of struggling students. She continues to teach regularly in classrooms, finding the experience essential for developing and testing new ideas and materials. The program was initially intended to provide math intervention for students who had fallen behind, yet many teachers reported using the modules in a wide variety of settings including whole-class instruction. The lessons are effective for building all students’ understanding, skills number sense, and engaged them with the mathematical practices.
Do The Math shifts the focus of instruction from simply covering content to uncovering essential math content (Burns, 2014). With this new focus the challenge of the teacher is not about finding better ways to explain new content but rather finding better ways of asking students to make sense of what they are learning for themselves (Burns, 2014). This shift from telling to asking is infused throughout all of the modules that comprise the Do The Math program.
The modular design of Do The Math provides flexibility, allowing for the program to be implemented in small-group settings to support struggling students, or in whole-class settings to build numerical understanding and reasoning skills. This flexibility also allows for it to be used in a variety of settings such as classrooms, resource rooms, extended day, and after school programs. The program can be used to supplement on-grade level instruction as well as an intervention for students who are multiple grade levels behind. The program aligns to Response to Intervention (RTI), a national framework for instruction and intervention.
The current version of Do The Math retains the core research principles from the original program and expands and enhances them with the use of lessons learned and the effective leveraging of current technologies. Now available for all tablets, the new Do The Math experience provides teachers and students with easy access to all lessons, interactive visual models, and games to engage and challenge learners within and beyond the walls of the classroom. Students have the flexibility to explore, make mistakes, and have fun with the range of tools and games designed to build their fluency and understanding of key concepts. Teachers can refine their instructional practices using a library of point-of-use resources designed by Marilyn Burns and Math Solutions.
Building upon the effective uses of technology, Do The Math’s HMH Teacher Central® is a new tablet-ready digital experience that provides teachers with virtual tools, games, and professional learning resources right at their fingertips. In addition, with the new HMH Student Central™, all of the students’ favorite games and hands-on materials are now available digitally to provide additional practice. ProgressSpace™ is another digital feature that offers an online assessment and reporting tool.
Do The Math rebuilds critical mathematical foundations for understanding by:
- Developing understanding of key concepts and skills with whole numbers and fractions—the essentials necessary for students to succeed in algebra and higher-level mathematics
- Providing lessons that balance developing understanding and learning procedures
- Strengthening students’ ability to make sense of concepts, solve problems, reason, and use appropriate tools
- Extending student practice and further increasing engagement through new online tools and interactive games
Designed to support struggling students in Grades 1–5+, Do The Math is organized into 13 scaffolded modules that focus on whole numbers and fractions. Each module contains 30 lessons. Students receive an assessment every fifth lesson to monitor progress. Additionally, students take a beginning- and end-of- module assessment to monitor growth.
Addition and Subtraction
NUMBER CORE
Number Core supports students’ success by rebuilding the foundations of Numbers and Operations. Students develop mental representations of quantity using the benchmark number of 5 and then 10, learn to think flexibly about how to compose and decompose numbers, and build facility with figuring sums to 20.
ADDITION & SUBTRACTION A: ADDITION WITH SUMS UP TO 100
Addition & Subtraction A builds a foundation for addition using two of the big ideas of mathematics:
- 10 is an organizer for the base-ten number system.
- Numbers can be composed and decomposed.
These big ideas help students to build place-value understanding and make sense of meaning behind the addition facts and calculations involving regrouping.
ADDITION & SUBTRACTION B: SUBTRACTION WITH NUMBERS UP TO 100
Addition & Subtraction B reinforces subtraction and addition as inverse operations. The major emphasis of this module is on helping students recognize the three meanings of subtraction in real-world contexts: take- away, missing part, and comparison. Students also learn three ways to compute differences between numbers from 0 to 100, and how to flexibly apply these strategies to solve contextual problems involving subtraction.
ADDITION & SUBTRACTION C: NUMBERS GREATER THAN 100
Addition & Subtraction C applies and extends the big ideas, concepts, and skills developed in earlier modules to calculations with greater numbers. Students use place value and explore the open number line to solve word problems with addition and subtraction involving numbers up to 999,999.
Multiplication
MULTIPLICATION A: BASIC CONCEPTS
Multiplication A provides visual and contextual models to help students understand the meaning of multiplication—a major building block for students that requires a shift from thinking additively to thinking multiplicatively.
MULTIPLICATION B: FACTS THROUGH 12 X 12
Multiplication B uses array models to represent the basic facts and show how the Commutative Property reduces the number of facts to learn. Applying the big idea that numbers can be decomposed to splitting array models lays the foundation for the Distributive Property and provides students with strategies for multiplying.
MULTIPLICATION C: FACTORS GREATER THAN 12
Multiplication C uses patterns; place value; and the Commutative, Associative, and Distributive Properties to help students make sense of and develop skills for multi-digit multiplication.
Division
DIVISION A: BASIC CONCEPTS
Division A focuses on the idea that division is the inverse operation of multiplication, eliminating the need to memorize division facts. Computational methods for solving a division problem are introduced contextually and concretely to help students understand the two meanings of division—sharing and grouping.
DIVISION B: FACTS THROUGH 100÷10
Division B applies understanding of the inverse relationship between multiplication and division to help students calculate quotients and remainders for two-digit numbers divided by two-digit divisors, and to solve word problems.
DIVISION C: DIVIDENDS TO 1000
Division C extends to dividing two- and three-digit dividends by two-digit divisors, engages students in exploring divisibility, and provides experiences with solving contextual problems involving greater numbers.
Fractions
FRACTIONS A: BASIC CONCEPTS
Fractions A provides students with concrete models that develop understanding of the meaning of fractions as equal parts of a whole. Teaching with fraction strips to model combining unit fractions, comparing fractional quantities to the benchmarks of ½ and 1, and identifying equivalent fractions is essential to help students give meaning to the abstract ideas of fractions.
FRACTIONS B: EQUIVALENCE AND COMPARISON
Fractions B develops six strategies for comparing and ordering fractions using reasoning with the support of fraction strips. Students extend their understanding of fractions of a whole to fractions as parts of sets, and learn to rename fractions as equivalent fractions.
FRACTIONS C: ADDITION AND SUBTRACTION
Fractions C extends students’ understanding of fractions to adding and subtracting fractions and using concrete models only to verify answers. Students use number sense to compute fractional sums and differences mentally, and use benchmark fractions to make estimates.
Do The Math provides teachers and students with easy access to all lessons, interactive visual models, and games to engage and challenge learners within and beyond the walls of the classroom. Students have the flexibility to explore, make mistakes, and have fun with the range of tools and games designed to build their fluency and understanding of key concepts. The program can flexibly adapt to a range of locally available technology including all tablets. ProgressSpace and its reporting functionality allow the teacherto monitor student understanding of key concepts periodically throughout a module. Teachers can also gauge student growth in their understanding through the use of pre- and post-module assessments.
For The Teacher
TEACHER BOOKCASE
The Teacher Bookcase contains all the teaching materials and professional resources needed for clear instructional guidance and lesson planning.
TEACHER GUIDE
The Teacher Guide provides all the information needed for lesson planning, monitoring student progress, and using both the Classroom Materials and mTools effectively.
PROFESSIONAL LEARNING GUIDE
The Professional Learning Guide from Math Solutions provides a comprehensive overview of the program architecture and instructional strategies.
HMH TEACHER CENTRAL FOR DO THE MATH
This new tablet-ready digital experience provides teachers with mTools, games, and professional learning resources right at their fingertips.
ANNOTATED WORKSPACE
The Annotated WorkSpace provides clear representations of model student answers to help teachers provide timely progress monitoring.
READ ALOUDS
Read alouds provide engaging children’s literature to support the instruction throughout the program.
For The Student
WORKSPACE
The WorkSpace® is designed to support students’ transition to independent work and to help teachers monitor students’ progress and understanding. The WorkSpace provides clear representations of model student answers to help teachers provide timely progress monitoring.
CLASSROOM MATERIALS BOX
The Classroom Materials Box provides hands-on resources and manipulatives that support and extend student learning throughout the modules.
HMH STUDENT CENTRAL
With HMH Student Central, all of the students’ favorite games and interactive visual models are now available digitally to provide additional practice.
MTOOLS
mTools allow teachers and students to use visual models to better understand foundational mathematical concepts and differentiate instruction on interactive whiteboards and tablets.
- Research-based visual models have been proven to help students build fluency and transition from concrete objects to abstract reasoning.
- Students may use a range of digital tools to explore multiple representations of a concept.
- Teachers may demonstrate using digital tools for older students, or to facilitate easier classroom management.
- Visual models are used and developed across modules to help students make connections and identify familiar mathematical structures.
About Marilyn Burns
Marilyn Burns is one of the most highly respected mathematics educators in the United States today. Over almost 50 years, she has educated children, conducted countless in-service workshops, written more than a dozen children’s books and numerous articles in professional journals, and created more than 20 professional development resources for teachers and administrators. In 1984, Marilyn founded Math Solutions Professional Development, an organization dedicated to the improvement of math instruction. She has received a number of awards, including the Glenn Gilbert National Leadership Award, given by the National Council of Supervisors of Mathematics, and the Louise Hay Award for Contributions to Mathematics Education, given by the Association for Women in Mathematics.
Marilyn Burns, along with a team of Math Solutions instructors with extensive classroom teaching experience, created the lessons in Do The Math. They discussed, wrote, debated, tested, rewrote, and refined the lessons to ensure that the content, pacing, and scaffolding were on target to meet the needs of struggling students. She continues to teach regularly in classrooms, finding the experience essential for developing and testing new ideas and materials.
About The Coauthors
VICKI BACHMAN
was a primary classroom teacher in Iowa City, Iowa, for more than 20 years and was most recently a math consultant for Grant Wood Area Education Agency in Cedar Rapids, Iowa. A Math Solutions in-service instructor, Vicki is the author of First Grade Math: A Month-to-Month Guide.
JANE CRAWFORD
is a recipient of the Presidential Award for Excellence in Teaching Mathematics, a Math Solutions consultant, and the author of Math by All Means: Money; she also taught in the Kalispell School District in Montana for more than 10 years and has a master’s degree in curriculum and instruction.
EUNICE HENDRIX-MARTIN
is a teacher at Carrillo Elementary School in Carlsbad, California, and has been teaching for 37 years. She is a curriculum developer and a conference presenter and has been a consultant for Math Solutions. Eunice has also authored math educational resources through Stenhouse.
LEO KOSTELNIK
is a K–8 principal, has been a classroom teacher in Grades 1–12, as well as a mentor teacher and professional development presenter.
MELODY RANDEL
has over 20 years of classroom teaching experience at the elementary, middle school, and university levels, and has been a Math Solutions consultant for over 17 years. She has a particular interest in the areas of teaching English learners and using differentiated instruction. She is one of the authors of the Math Reasoning Inventory® (MRI).
SUSAN SCHARTON
has over 30 years of experience teaching at the elementary and university levels and is currently a Math Solutions consultant. She completed her EdD in Teaching and Learning in 2007. Her book, Teaching Number Sense, was published in 2005.
MALLIKA SCOTT
is the cofounder of S&S Math Services, has been a classroom teacher in Grades 2–8 as well as a math coach, mentor teacher, professional development presenter, and conference speaker.
DANIELLE WEILL
has over 18 years of experience teaching at the upper elementary and middle school levels. She is currently a 6th grade teacher and math leader at her school in California, in addition to working as a Math Solutions consultant. She worked closely with Marilyn Burns during the development of the Teaching Arithmetic: Introducing and Extending Fractions books.
MARYANN WICKETT
is a former elementary classroom teacher and mathematics staff developer in San Marcos Unified School District in San Marcos, California, and is a recipient of the Presidential Award for Excellence in Science and Mathematics Teaching. She is also a workshop leader, conference speaker, and Math Solutions consultant.
LYNNE ZOLLI
is a classroom teacher in Grades 1–6 and has also been a mentor teacher, professional development leader, and conference speaker. Lynne has served as a grant writer and written Math Solutions professional books.
In the years since the original release, Do The Math has been proven to be successful in addressing the key challenges that American students face.
The program’s instructional design applies what is known about reaching a wide variety of students who struggle with math to help them achieve proficiency with arithmetic concepts and skills.
Do The Math incorporates the following guiding principles:
- Teaching for Understanding: Step-by-step lessons help students develop understanding, learn new mathematical skills, see relationships, and make connections.
- Scaffolded Content: Breaking down the content into chunks makes the mathematics more accessible to students.
- Multiple Strategies: Exploring different strategies for developing concepts and skills builds students’ mathematical reasoning.
- Mathematical Thinking: Standards help develop mathematical expertise and habits of mind in all students.
- Classroom Routines: Routines such as “think, pair, share” promote engagement and deepen student understanding, particularly among English learners.
- Independent Student Work: Assignments provide students with opportunities to practice, strengthen, and extend their learning.
- Vocabulary and Language: Explicit vocabulary instruction helps students communicate effectively about the math they are learning.
- Assessment and Differentiation: Ongoing assessment and progress monitoring helps teachers meet individual student needs.
Teaching for understanding describes an approach to mathematics instruction in which the teacher: 1) demonstrates and provides clear models of thinking through solving a problem or learning a skill, 2) supports students to understand connections and articulate relationships, 3) provides extensive practice with timely feedback, and 4) encourages students to verbalize their thinking. Teaching for understanding is accomplished through explicit, intentional instruction that addresses the diverse needs of students.
Research Foundations
- A meta-analysis of 55 studies comparing instruction conducted with concrete manipulatives versus control conditions using only abstract representations concluded that the effective use of manipulatives in mathematics instruction has a positive effect on student learning (Carbonneau, Marley, & Selig, 2013).
- As students use manipulatives to explore mathematical concepts, it is important that pictorial representations are used to bridge their reasoning from concrete to abstract (Battista, 2012; Bray & Abreu-Sanchez, 2010).
- Feedback is essential for providing information to a student on their progress toward a particular goal. An essential element to the success of this feedback is timing. The earlier a student can get that feedback, the better (Wiggins, 2012).
- Explicit instruction with students who have mathematical difficulties has shown consistently positive effects on performance with word problems and computations (National Mathematics Advisory Panel, 2008).
- Establishing clear and explicit learning goals is essential for the teaching of mathematics (Hiebert et al., 2007).
- Teaching underlying mathematical foundations through explicit instruction and then providing students with the opportunity to work on relevant problems produced positive gains when compared with traditional instruction (Gersten, 2003).
- Explicit concrete-to-representational-to-abstract sequenced instruction was shown to be an effective pedagogical strategy for building mathematical knowledge and skills (Witzel, Mercer, & Miller, 2003).
- Reports from the National Follow-Through Project showed that explicit instruction was associated with achievement in both basic skills and math concepts (Hall, 2002).
How Do The Math Delivers
Do The Math supports teaching for understanding through the use of explicit instruction intentionally designed to model mathematical thinking, connect concepts to their mathematical representations, and introduce appropriate language. In Do The Math, explicit instruction does not mean to imply “teaching by telling.” When learning requires understanding of logical mathematical processes, it is essential that the explicit instruction presents carefully sequenced experiences through which the students develop concepts, learn skills, see relationships, and make connections. However, when students are required to learn social conventions, such as vocabulary and mathematical symbols, the explicit instruction imparts the necessary and appropriate information.
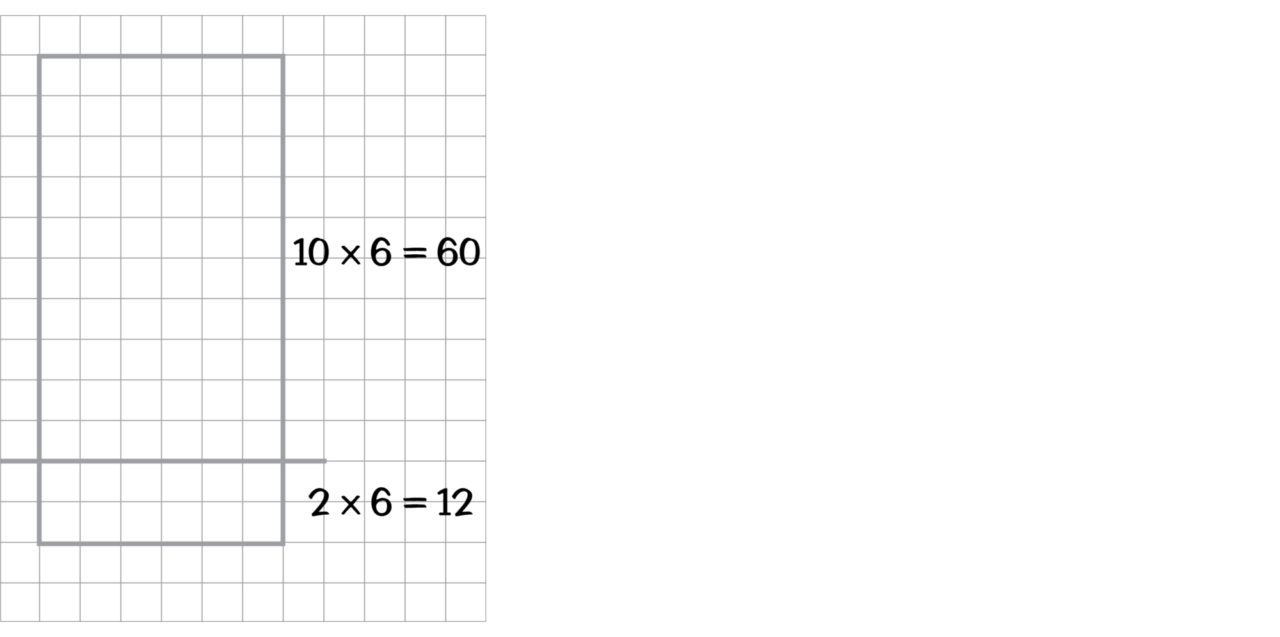

Scaffolding is the systematic process of analyzing the content and partitioning it into small manageable chunks for the purpose of planning and delivering instruction that facilitates students’ learning. Scaffolded content is at the heart of planning instruction for struggling students. Research shows that scaffolding content to inform instruction benefits all students, and particularly students with learning disabilities.
Research Foundations
- The importance of scaffolding instruction encompasses many domains and populations of students whether they are general education or at-risk students. Teachers in pre-service programs also benefit from scaffolded instruction in their acquisition of pedagogical content knowledge (Visnovska & Cobb, 2015; Nason, Chalmers, & Yeh, 2012).
- Scaffolding can provide an aid for students’ development of important critical thinking skills as it provides the necessary supports for students as they engage in more complex cognitive processes (Belland, 2014).
- Although the specific strategies used to implement scaffolding may vary somewhat a review of 10 years of scaffolding research found the practice to be effective for both metacognitive and cognitive student outcomes (Pol, Volman, & Beishuizen, 2010).
- Scaffolding allows the class as a whole to move toward deeper levels of understanding key mathematical concepts. It also allows students to work individually on material that is appropriate for their particular level of understanding (Williams, 2008).
- By providing the necessary supports, scaffolding allows students to achieve a greater sense of ownership of their learning (Hyde, 2006).
- Scaffolding is one of the principles of effective instruction that enables teachers to accommodate individual student needs (Kame’enui, Carnine, Dixon, Simmons, & Coyne, 2002).
- Scaffolded instruction helps students became more independent learners. “Scaffolding principles and techniques can guide teachers to assist students on any grade level to become more independent learners” (Larkin, 2001, p. 34).
- Three strategies for scaffolding content—organization of concepts, sequencing, and chunking—support teaching for conceptual understanding (Grouws & Cebulla, 2000).
- Scaffolding is the “role of teachers and others in supporting the learner’s development and providing support structures to get to that next stage or level,” according to Vygotsky (Raymond, 2000, p. 176).
- A synthesis of investigations into instructional techniques for students with learning disabilities shows scaffolding to be among the most effective approaches (Gersten, 2003).
- Students learn better when new knowledge is connected to things that they already know and understand (Hiebert & Carpenter, 1992; Hiebert et al., 1997).
How Do The Math Delivers
Do The Math focuses on the basics of Numbers and Operations with lessons that build accuracy, efficiency, and understanding. All lessons have been carefully designed and sequenced to align with the scaffolding of the content, and then paced to ensure student success.

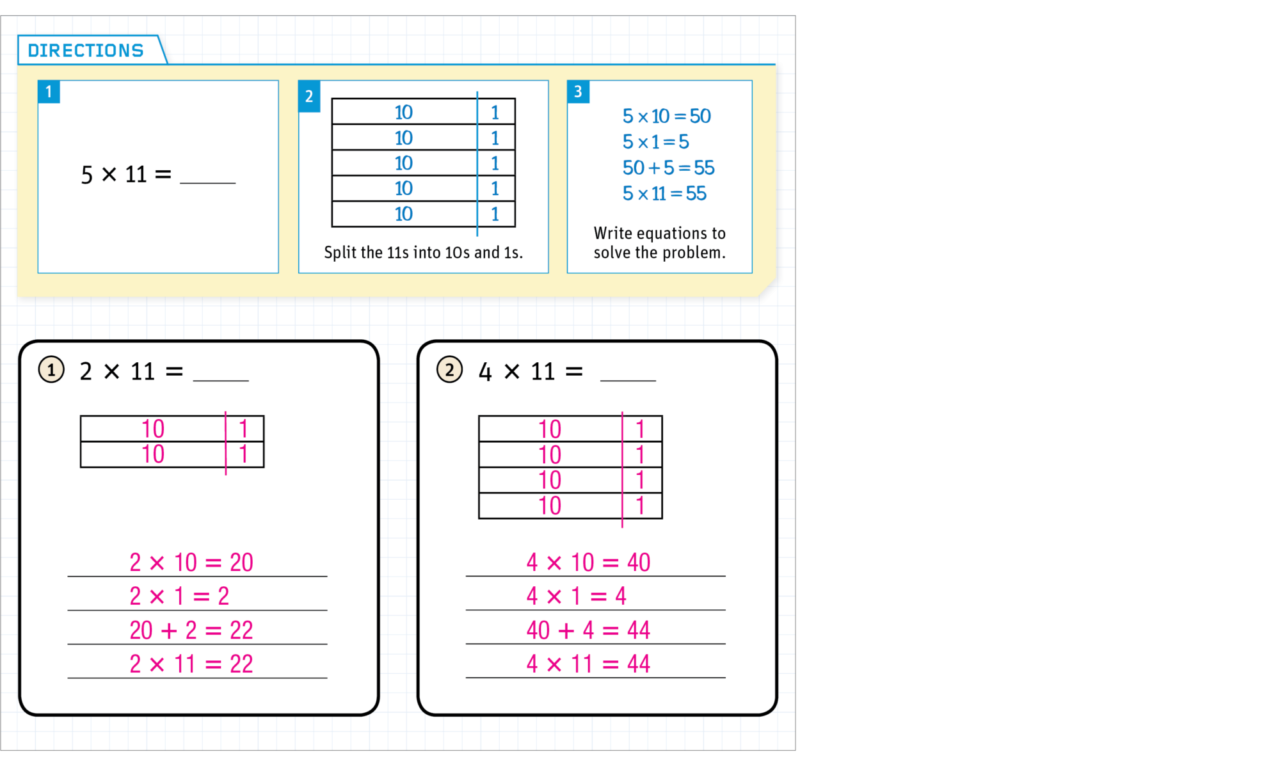
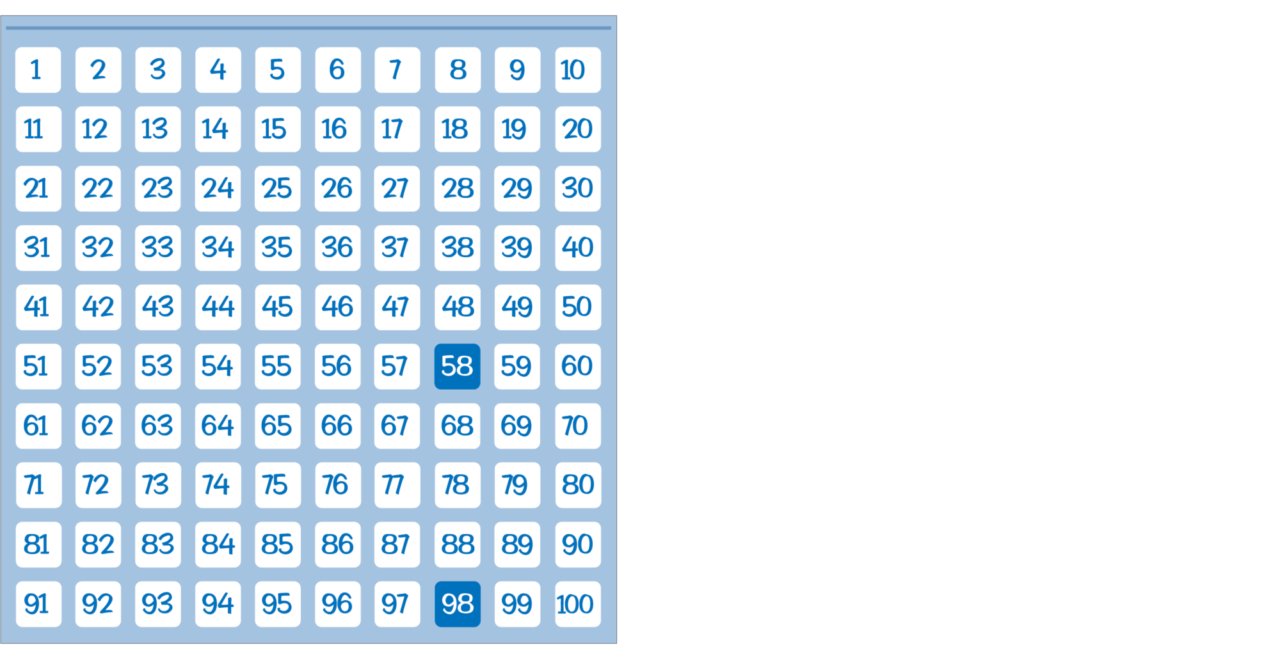
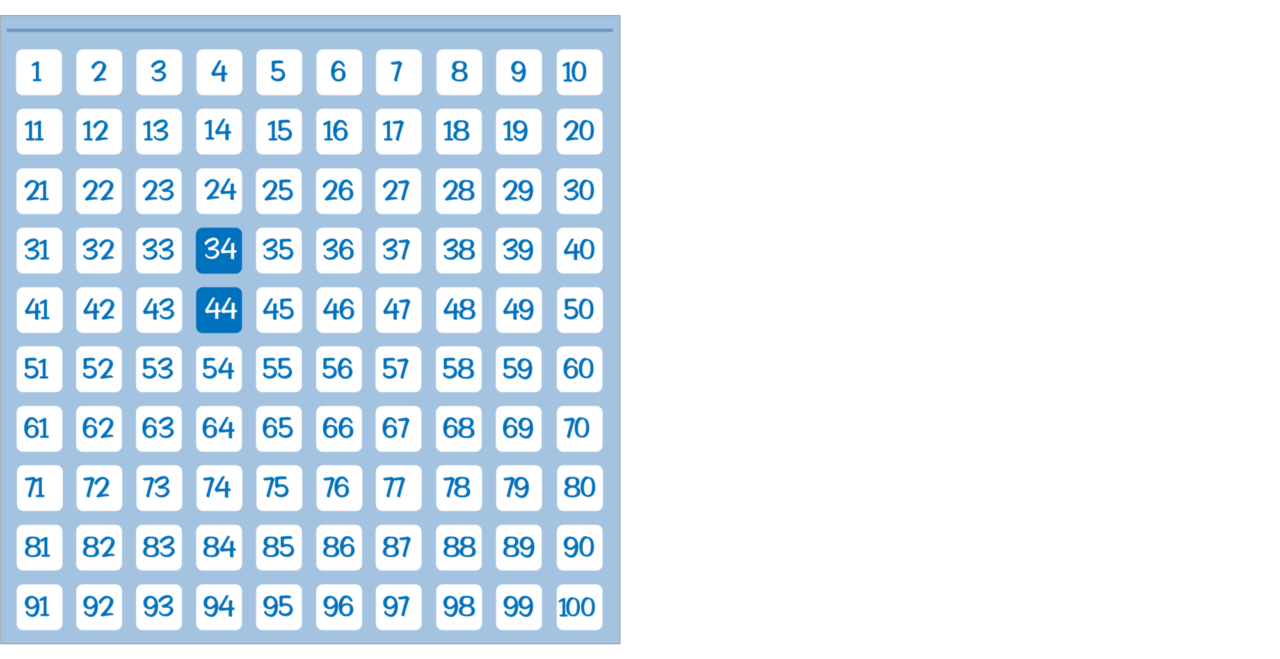
In Addition & Subtraction A, Lesson 18: Students use the hundred-pocket chart to find patterns as they add multiples of 10. This is helpful for students, as they use the open line to add, making jumps of 10s in later lessons in the module.
Multiple strategies are essential to ensure that all students build number sense, develop skills, deepen their mathematical understanding, and make connections. Using multiple strategies such as modeling, engaging in discussions, and viewing and creating visual representations to teach mathematics ensures that students have a deep understanding of each skill and concept, rather than a shallow or incorrect notion.
Research Foundations
- Making comparisons has been shown in cognitive psychology to be an effective process for the classroom. Reviewing and comparing multiple strategies for solving problems helps increase student understanding by improving procedural flexibility (Star, Pollack, Durkin, Rittle-Johnson, Lynch, Newton, & Gogolen, 2015; Rittle-Johnson & Star, 2011).
- “Effective teaching of mathematics engages students in solving and discussing tasks that promote mathematical reasoning and problem solving and allow multiple entry points and varied solution strategies” (NCTM, 2014, p. 10).
- The National Council of Supervisors of Mathematics (NCSM, 2013) recommends that teachers consistently use manipulatives to build conceptual understanding of mathematics.
- Manipulatives can help students build links between the object, the symbol, and the mathematical idea being represented (National Research Council, 2001) and are a useful strategy for helping students to build a foundation in mathematics, particularly for students who have previously struggled with mathematics (NCSM, 2013).
- Studies that included visual representations produced significant positive effects for students with learning disabilities, and for low- achieving students (National Mathematics Advisory Panel, 2008).
- Manipulative materials help students make sense of abstract ideas, provide students with ways to test and verify ideas, are useful tools for solving problems, and make mathematics learning more engaging and interesting by lifting mathematics off textbook and workbook pages (Burns, 2007).
- The American Mathematical Society identified teaching using multiple strategies as a common area of agreement in a concept paper (Ball et al., 2005).
- A summary of research suggests that the development of practical meaning for mathematical concepts is enhanced through the use of manipulatives (Sabean & Bavaria, 2005).
- Visual representations help students advance their understanding of mathematical concepts and procedures, make sense of problems, and engage in mathematical discourse (Arcavi, 2003; Stylianou & Silver, 2004).
- The use of contextually based problems and games provides intrinsic motivation for students (Kamii, 2000).
- Multiple means of content representation, expressing learned content, and content engagement are cornerstones in Universal Design for Learning, a set of principles designed to make learning universally accessible to all learners (Rose & Meyer, 2000).
How Do The Math Delivers
In Do The Math, lessons engage students with concepts and skills in multiple ways using concrete manipulative materials, games that reinforce concepts and provide practice, selected children’s literature that offers a context for mathematical concepts and skills, and visual representations to help students represent their thinking.
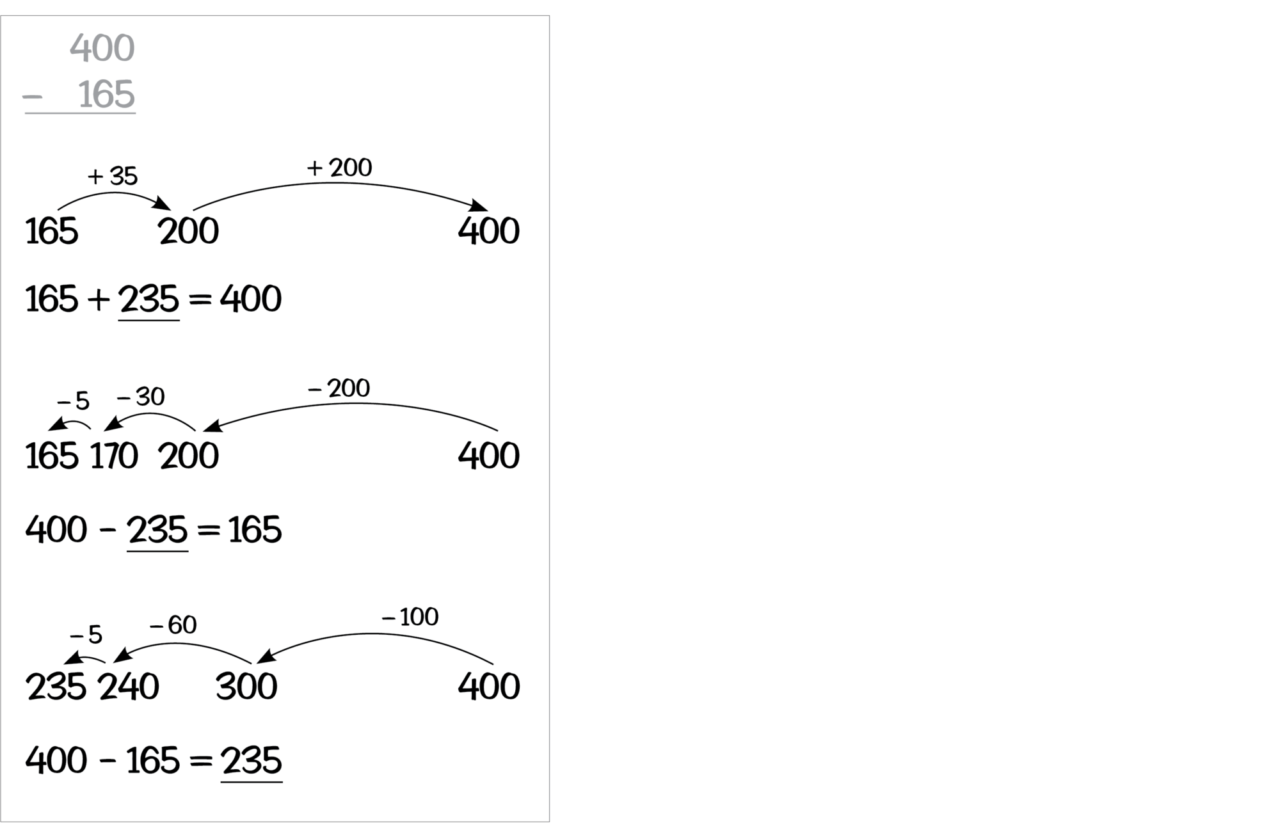
Do The Math is focused on developing the early habits of mind necessary to foster the ongoing progress toward mathematical proficiency. Building these skills is fundamental in developing students into mathematical thinkers. Students must be able to persevere, reason abstractly, use mathematics to model and solve real-world problems, and strategically apply mathematical and practical tools.
Research Foundations
- In order to learn mathematics and then have the ability to express or apply that knowledge in unique situations takes more than just exposure to facts, definitions, rules, and procedures. Students need to go beyond solving simple word problems and must explain their thinking and enter into productive mathematical dialog (Seeley, 2014).
- The What Works Clearinghouse identified 16 studies that demonstrate the positive effects of encouraging children to view and describe their world mathematically. Students begin by using informal representations, gradually moving to more formal with the addition of mathematical vocabulary (Frye, Baroody, Burchinal, Carver, Jordan, & McDowell, 2013).
- To develop mathematical proficiency, the Standards for Mathematical Practice must become an integrated part of student learning (Confrey & Krupa, 2010).
- External representations, such as models, help students understand abstract mathematics (Gersten et al., 2009). These models assist students in moving through a progression from concrete to pictorial to abstract representations of mathematical content (Wong, 2004).
- Effective teachers provide students with opportunities to develop procedural fluency and conceptual understanding (Hiebert & Grouws, 2007).
- The ability to understand and use language—both conversational and mathematical—is imperative to the development of mathematical concepts (Lager, 2007) and necessary for abstract reasoning in mathematics (Khisty & Morales, 2004).
- Modeling plays a vital role in Singapore’s national mathematics curriculum. Modeling provides students with concrete, pictorial, and abstract approaches to problem solving, ensuring the development of mathematical understanding and competencies (Ministry of Education Singapore, 2006).
- The Standards support students to develop conceptual understanding, procedural fluency, strategic competence, and adaptive reasoning (NRC, 2001).
How Do The Math Delivers
In Do The Math, students are asked to solve real world problems that are presented in ways that are accessible to them. When solving these problems, they are asked to represent them in multiple ways both mathematically and with the use of concrete and digital manipulatives. In order to accomplish this successfully, students must draw from prior knowledge and communicate their ideas mathematically when working in pairs and independently when applying their reasoning individually.
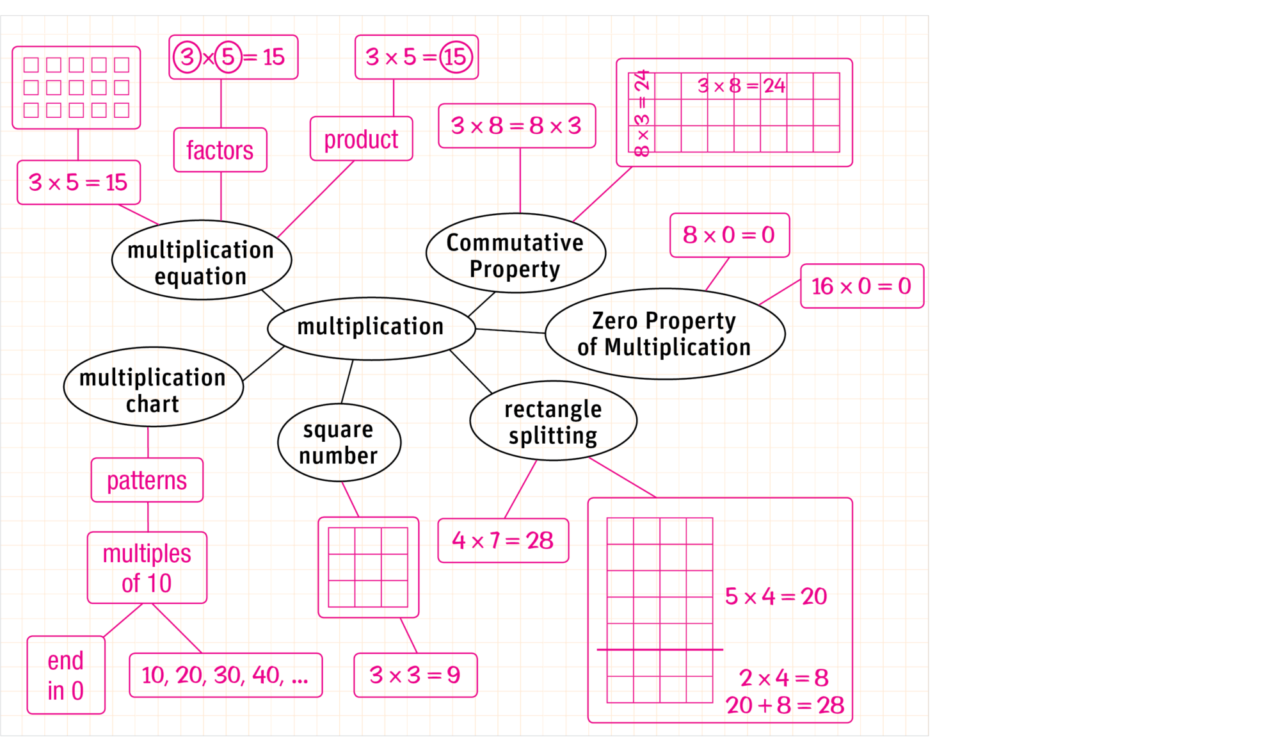

When students voice their mathematical ideas and explain them to others, they extend and deepen their understanding of the mathematics. Using classroom routines such as “think, pair, share” encourages students to interact and to take responsibility for their own learning as they discuss their thinking. Expressing math knowledge verbally to a partner is particularly valuable for many students who are developing English language skills.
Research Foundations
- Teachers should take opportunities to address tensions around language and mathematical content, to establish a mathematical discourse in the classroom community, and to foster the development of academic language and mathematical precision among students (Moschkovich, 2012).
- The way students learn mathematics is fundamentally impacted by what happens in the classroom and how teachers and students interact with the curriculum (Ball & Forzani, 2011).
- Feedback and classroom discourse can have a lasting impact on how students view intelligence (Burnett & Mandel, 2010).
- Programs that engage students in discussions about how people learn, how to overcome obstacles to learning, and how to create a community of learners have shown an increase in students’ confidence, motivation, and persistence, and a strengthening in students’ beliefs that they have control over their intelligence (NCSM, 2010).
- The development of mathematical concepts is assisted by students’ abilities to understand and use mathematical language (Lager, 2007).
- Teaching is composed of classroom interactions—between the individuals in the classroom and between those individuals and mathematics—that facilitate student learning (Hiebert & Grouws, 2007; Artzt & Armour-Thomas, 1999).
- When students explain their thinking, either in pairs or small groups, they are forced to reflect on their own reasoning and to organize their thoughts clearly in order to communicate them to others (Chapin et al., 2003).
- Classroom interactions flow from the culture and norms established by the classroom teacher (NRC, 2001) and directed by the learning goals (Stein, Smith, Henningsen, & Silver, 2000).
- Learning with understanding can be further enhanced by classroom interactions, as students propose mathematical ideas and conjectures, learn to evaluate their own thinking and that of others, and develop mathematical reasoning skills (Hanna & Yackel, 2000).
- Structuring instruction around carefully chosen problems, allowing students to interact when solving problems, and then providing opportunities for them to share their solution methods results in increased achievement on problem-solving measures (Grouws & Cebulla, 2000).
- Several studies show that collaborative learning methods such as peer-mediated instruction produces increased achievement and conceptual understanding for students with and without disabilities (Fuchs et al., 1997).
How Do The Math Delivers
In Do The Math, student interaction is built into the program.
- One essential routine that encourages active student engagement is “think, pair, share”. Having students talk in pairs provides them with a safe way to share ideas, brainstorm, and practice what they will say when they share with the larger group.
- Partner interaction is always encouraged when students are released to work independently in their WorkSpace books or tablets to build students’ confidence and encourage them to justify their reasoning.
- Games are carefully introduced and appropriate to the skills being taught. They encourage active engagement and provide practice.
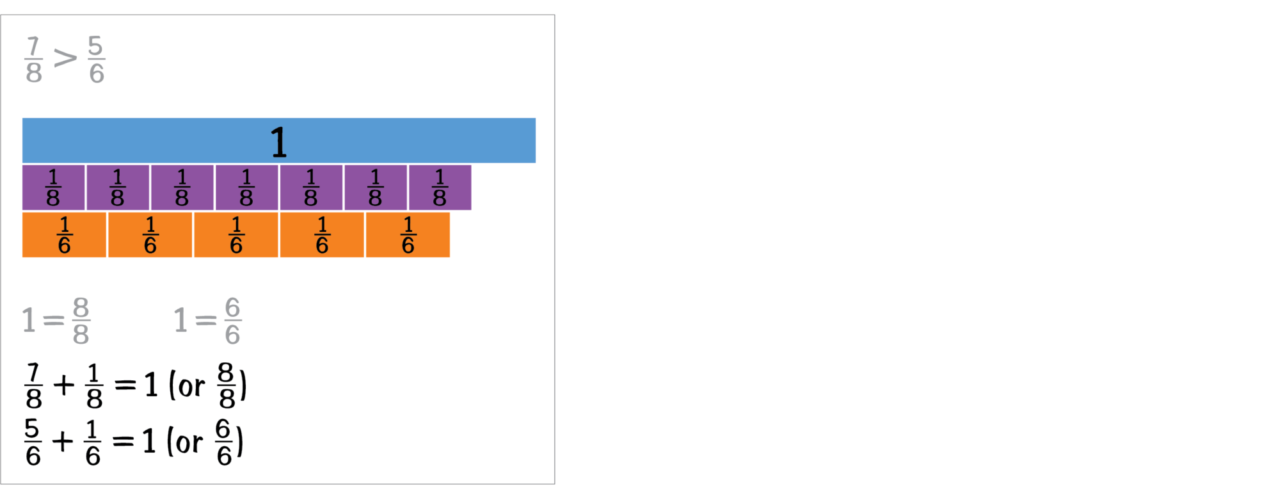

Independent student work is most effective when it provides students opportunities to use their developing conceptual understanding and number sense, and is connected to previously learned concepts and skills. Regular practice is essential, and intervention students typically need more practice. Independent work, such as practice, provides students opportunities to strengthen and reinforce their learning as they connect new understanding to existing knowledge.
Research Foundations
- Independent student practice is an essential ingredient for reinforcing knowledge and procedures and for building fluency. This practice can take place inside or outside the class and should be tied to instructional objectives (Rosenshine, 2012).
- Underserved students benefit from technology that emphasizes one-on-one experience with content. A significant force factor in this effect is the increased level of interactivity this learning environment affords. The increased interactivity allows students more opportunities for exploration and examining complex tasks in multiple ways (Zielezinski & Darling-Hammond, 2016; Elam, Donham, & Soloman, 2012).
- A review of 26 high-quality studies indicates that explicit instruction with extensive practice is effective for students with learning disabilities and for low-achieving students (National Mathematics Advisory Panel, 2008).
- Researchers have found that students’ conceptual understanding and problem-solving skills improve when they are encouraged to make sense of mathematics by writing about their mathematical thinking (Putnam, 2003).
- Repeated practice and application are essential to learning (Gee, 2003; Marzano, 2002; Pressley, 1995).
- In a report to the U.S. Department of Education, two specific strategies were cited that help students gain a deeper understanding of a topic. One strategy is targeted assignments that focus on specific elements of a complex skill and its practice. The other is practice that focuses on building conceptual understanding related to skills and procedures (Marzano et al., 2000).
- When students understand what is expected of them, they have increased motivation (Reiser & Dick, 1996).
- Mathematics makes more sense and is easier to remember and to apply when students connect new knowledge to existing knowledge in meaningful ways (Schoenfeld, 1988).
- An important reason to practice mathematics is to strengthen and reinforce what has already been learned. Studies about the specific nature of practice suggest that many repeated practice sessions are required for students to attain high levels of competence (Newell & Rosenbloom, 1981).
How Do The Math Delivers
In Do The Math, independent student work is an essential part of every lesson. The written practice in the WorkSpace is always similar to what students experienced during the lesson. The practice is carefully sequenced so that no new knowledge or skill is required in order for the student to be successful. Practice is supported through visual directions on the WorkSpace pages for those students who need a point-of-use reminder of the steps involved.
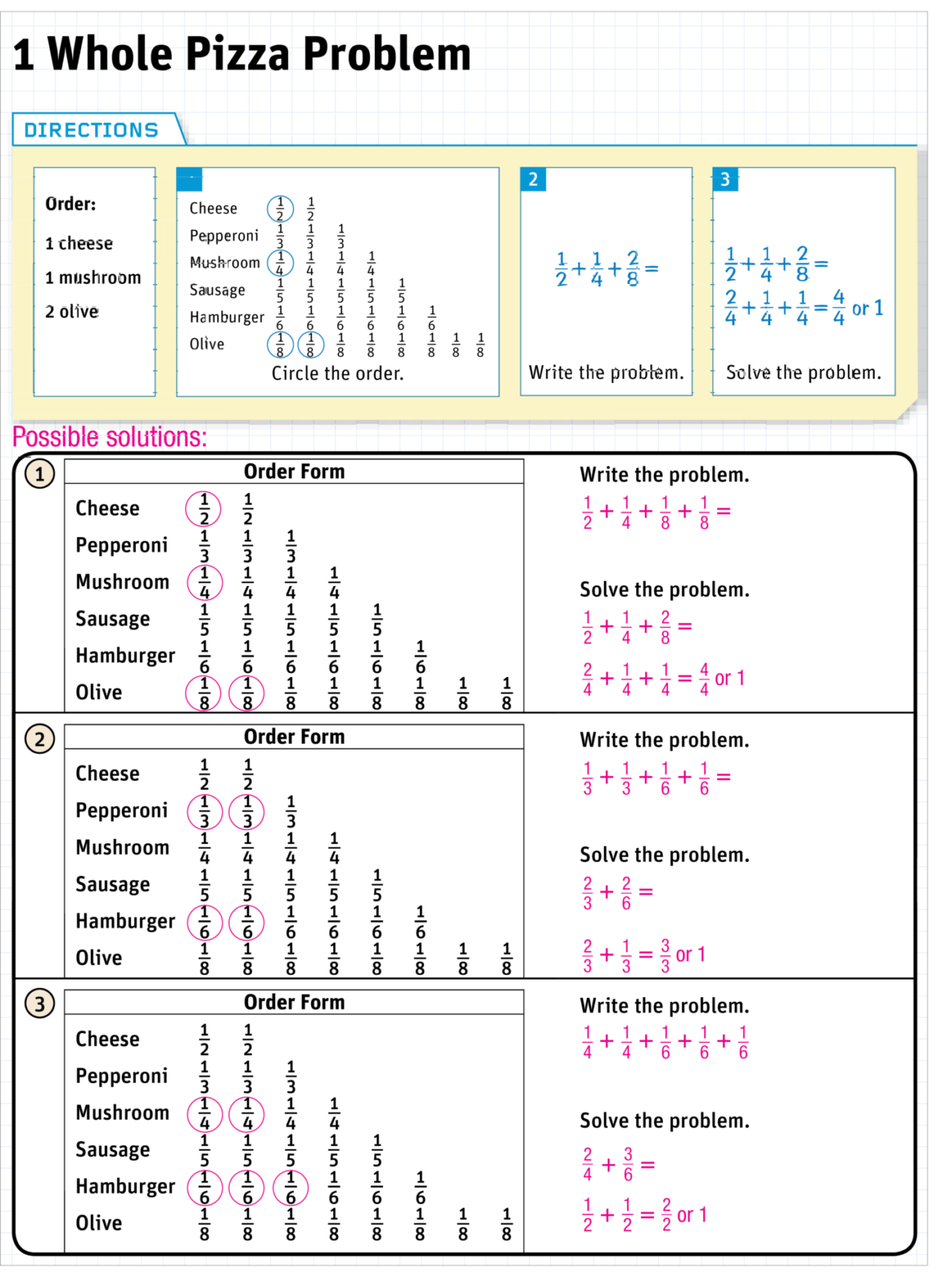
Teaching students correct mathematical language gives them the tools to articulate their mathematical thinking coherently and precisely. Students incorporate the new vocabulary into their own language as they explain their thinking to each other or in whole-group settings. Explicitly teaching vocabulary and then using the words frequently in class discussions benefits all learners and encourages them to use the words when they are explaining their reasoning to each other.
Research Foundations
- By learning the language of mathematics with both vocabulary and symbols, native English speakers and English learners can learn mathematics together (Razfar, Khisty, & Chval, 2011).
- Teachers must be cognizant of their lessons’ linguistic demands on English learners (Math Solutions, 2011).
- To support the mathematical learning of English learners, instruction should begin with stated content and language goals, build on student cultural context, limit unnecessary language, purposefully develop vocabulary, and utilize cooperative groups as safe learning spaces (Van de Walle, Karp, & Bay-Williams, 2010).
- Through classroom discourse, all aspects of mathematical thinking can be discussed, dissected, and understood. Dialogue in the classroom provides access to ideas, relationships among those ideas, strategies, procedures, facts, mathematical history, and more (Chapin, O’Connor, & Anderson, 2009).
- Instruction that emphasizes vocabulary and domain-specific communication skills can support learning for all students. Explicit vocabulary instruction is important because students may have existing notions about words such as product, factor, times, and sum that do not align with the mathematical meaning of these terms (Ball et al., 2005; Allen, 1988; Garrison & Mora, 1999).
- Based on a study of mathematical discourse between teachers and students in math classrooms, it was demonstrated that confusion arises when the precise meaning of mathematical words is not established (Raiker, 2002).
- Systematic vocabulary instruction in which new vocabulary is directly defined increases the likelihood that students will learn the terms (Marzano, 2002).
- English learners who are struggling with math must overcome confusions between trying to achieve mathematical understanding and trying to learn mathematical procedures (Frederickson & Cline, 2002).
- Teacher modeling of mathematical discourse provides students with the opportunity to incorporate mathematical language into their own communications about the mathematics they encounter (Khisty & Chval, 2002).
- The language of mathematics is an important component of instruction because students build their understanding as they process ideas through language (Thompson & Rubenstein, 2000).
- When English learners are presented with mathematics instruction and techniques that make concepts and operations comprehensible and are also presented with additional language and academic support that meets their needs, they are able to be successful. Additionally, working in groups can allow students to develop listening and speaking skills while increasing mathematical understanding (Garrison & Mora, 1999).
How Do The Math Delivers
In Do The Math, vocabulary is introduced after students experience and develop a firm understanding of the mathematical concept so that they can anchor the word in their understanding. The meaning of a key vocabulary word is explicitly taught using the routine of see it, hear it, say it, write it, and read it. The word is recorded on a math vocabulary chart with examples so that students may refer to it as needed. Students read the meaning in their own student glossaries and record the meaning with an example in their WorkSpace. Students hear the word used frequently by the teacher and naturally begin to incorporate it into their own explanations as they talk to their partners and share their reasoning with the whole group.
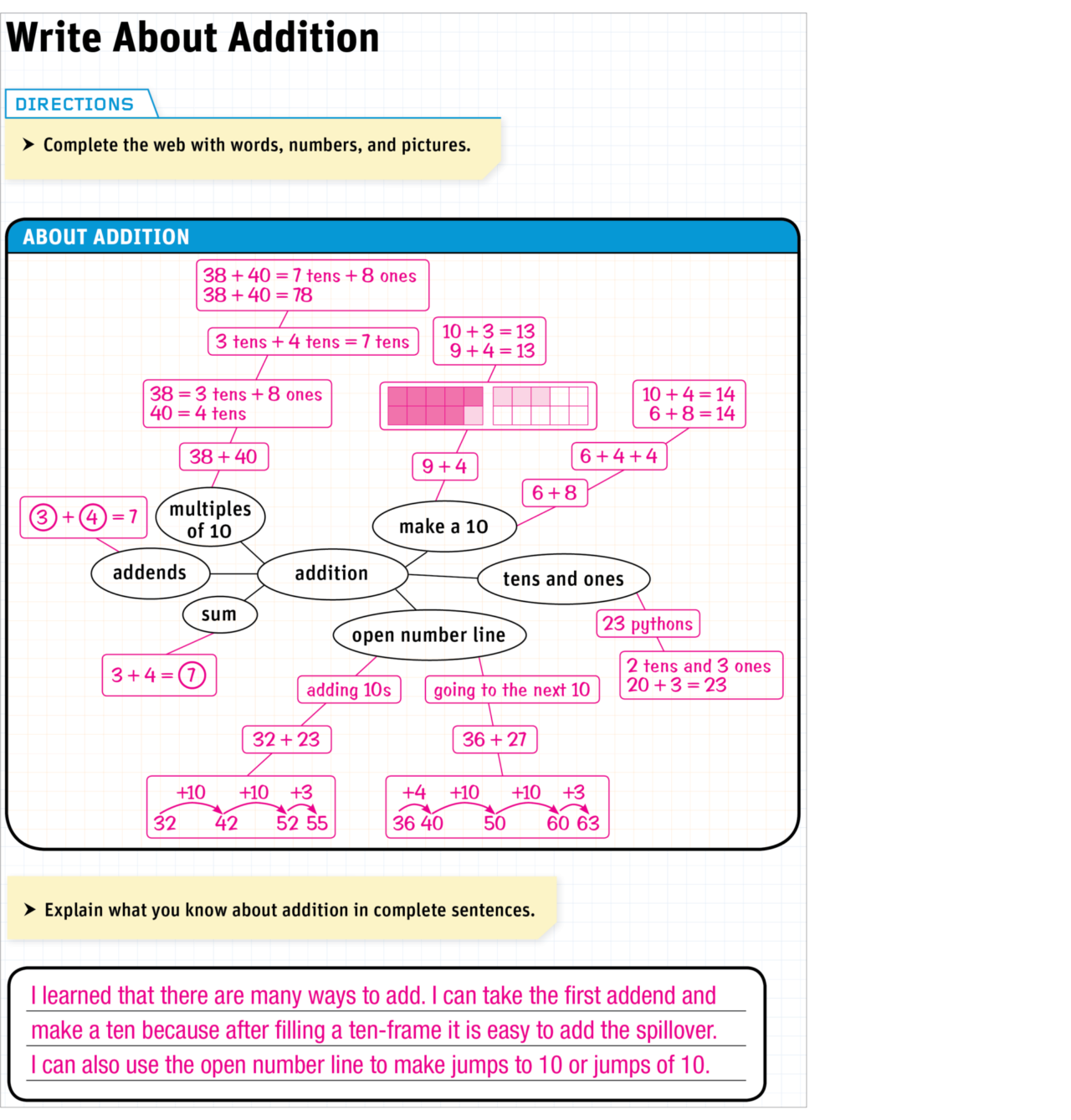

Probing students’ internal reasoning processes reveals both their grasp of foundational concepts as well as their misconceptions. Do The Math provides guidance for teachers to assess students’ understandings during instruction and immediately address misconceptions. This allows teachers to differentiate instruction for all students: those who need additional help and those who are ready for a challenge.
Research Foundations
- “An excellent mathematics program ensures that assessment is an integral part of instruction, provides evidence of proficiency with important mathematics content and practices, includes a variety of strategies and data sources, and informs feedback to students, instructional decisions, and program improvement” (NCTM, 2014, p. 89).
- Providing effective instructional practice should be the primary function of assessment to ensure mathematical success for all students (NCTM, 2014).
- The WWC educator’s practice guide points to the importance of providing routine targeted assessments to gauge student learning & progress and using the data to inform instruction (Frye, Baroody, Burchinal, Carver, Jordan, & McDowell, 2013).
- Learning is enhanced when instruction accommodates the differences in learning needs among individual children (Sousa & Tomlinson, 2011).
- A comprehensive assessment system integrates assessment and instruction, so that educators can continually use data to ensure they are meeting the needs of all students (National Center on Response to Intervention, 2010; Smith, 2010).
- Data collected through progress-monitoring should provide a clear profile of students’ strengths, weaknesses, and needs, and should be linked with resources for providing targeted follow-up instruction and intervention (Carnegie Council on Advancing Adolescent Literacy, 2010; National Joint Committee on Learning Disabilities, 2008; Vaughn & Denton, 2008).
- Findings from a review of the high-quality studies of assessment suggest that use of formative assessment benefited students at all ability levels. When teachers use the assessment data to provide differentiated instruction, the combined effect is significant (National Mathematics Advisory Panel, 2008).
- Ongoing assessment and progress monitoring are vital to documenting student growth and informing instruction (National Joint Committee on Learning Disabilities, 2008; Fisher & Ivey, 2006; Stecker, Fuchs, & Fuchs, 2005; Torgesen, 2002).
- Collecting data on student progress to drive instruction is vital to documenting student growth and determining the need for modifying instruction (Stecker, Fuchs, & Fuchs, 2005).
- Providing teachers with specific information on how each student is performing consistently enhances students’ mathematics achievement (Baker et al., 2002).
How Do The Math Delivers
In Do The Math, lessons are carefully built on scaffolded content with attention to the common misconceptions of students who are in need of intervention. Ongoing assessment and suggestions for differentiation are integral to the program.
- The Beginning-of-Module Assessment establishes a benchmark with which to measure each student’s mathematics growth after completing the module.
- Formative Assessment through daily observations gives students the prompt attention that will enable them to complete math assignments successfully.
- Progress Monitoring, which occurs every fifth lesson, is followed by suggestions for differentiating instruction—what to do for the students who need additional support and for those ready for a challenge.
- ProgressSpace features an End-of-Module Assessment, or Summative Assessment, which provides an opportunity to measure student growth and an opportunity to give continued support to those who need it.


- Report Type: Efficacy Study, Study Conducted by Third Party
- Grade Level: Elementary
- Region: Southeast
- District Urbanicity: Urban
- District Size: Large
- Report Type: Efficacy Study
- Grade Level: Elementary
- Region: Northeast
- District Urbanicity: Urban
- District Size: Large
- Report Type: Efficacy Study
- Grade Level: Elementary
- Region: West
- District Urbanicity: Suburban
- District Size: Large
- Report Type: Efficacy Study
- Grade Level: Elementary, Middle
- Region: Southeast
- Population: Students with Disabilities
- District Urbanicity: Suburban
- District Size: Large
Allen, F. B. (1988). Language and the learning of mathematics. A paper presented at the National Council of Teachers of Mathematics Annual Meeting, Chicago, IL.
Arcavi, A. (2003). The Role of Visual Representations in the learning of mathematics. Educational Studies in Mathematics, 52(3), 215–41.
Artzt, A. F., & Armour-Thomas, E. (1999). A cognitive model for examining teachers’ instructional practice in mathematics: A guide for facilitating teacher reflection. Educational Studies in Mathematics, 40(3), 211–235.
Askew, M. (2002). The changing primary mathematics classroom—the challenge of the National Numeracy Strategy. In L. Haggerty (Ed.), Aspects of teaching secondary mathematics: Perspectives on practice. London: Routledge Falmer.
August, D., & Hakuta, K. (1997). Improving schooling for language-minority children. Washington, DC: National Academy Press.
Baker, S., Gersten, R., et al. (2002). A synthesis of empirical research on teaching mathematics to low-achieving students. The Elementary School Journal, 103(1), 51–73.
Ball, D. L., & Forzani M. (2011). Building a Common Core for learning to teach and connecting professional learning to practice. American Educator, 35(2), 17–21.
Ball, D. L., Mundy, J. F., et al. (2005). Reaching for common ground in K–12 mathematics education. Notices of the AMS, 52(9), 1055–1058.
Battista, M.T. (2012) Cognition-based assessment & teaching of fractions: Building on students’ reasoning. Portsmouth, NH: Heinemann.
Bay-Williams, J., Duffett A., & Griffith, D. (2016). Common Core math in the K–8 classroom: Results from a national teacher survey. Washington, DC: Thomas B. Fordham Institute.
Belland, B. R. (2014). Scaffolding: Definition, current debates, and future directions. In J. M. Spector, et al. (Eds.), Handbook of research on educational communications and technology. New York: Springer
Bray, W. S., and Abreu-Sanchez, L. (2010). Using number sense to compare fractions. Teaching Children Mathematics (17), 90–97.
Brooks, M. (2009). Drawing, visualization, and young children’s exploration of “big ideas,” International Journal of Science Education, 3(1), 319–341.
Burnett, P. C., & Mandel, V. (2010). Praise and feedback in the primary classroom: Teachers’ and students’ perspectives. Australian Journal of Educational & Developmental Psychology, 10, 145–154.
Burns, M. (2007). About teaching mathematics: A K–8 resource (3rd Edition). Sausalito, CA: Math Solutions.
Burns, M. (2014). Uncovering the math curriculum. Educational Leadership, 72(2), 64–68.
Carbonneau, K. J., Marley, S. C., & Selig, J. P. (2013). A meta- analysis of the efficacy of teaching mathematics with concrete manipulatives. Journal of Educational Psychology, 105(2), 380–400.
Carnegie Council on Advancing Adolescent Literacy. (2010).Time to act: An agenda for advancing adolescent literacy for college and career success. New York: Carnegie Corporation of New York.
Cawley, J., Parmar, R., Yan, W. F., & Miller, J. (1996). Arithmetic computation performance of students with learning disabilities: Implications for curriculum. Learning Disabilities: Research and Practice, 13(2), 68–74.
Chapin, S., O’Connor, C., & Canavan Anderson, N. (2003). Classroom discussions: Using math talk to help students learn. Grades K–6. Sausalito, CA: Math Solutions Press.
Chapin, S. H., O’Connor, C. O., & Anderson, N. C. (2009). Classroom discussions: Using math talk to help students learn. Sausalito, CA: Math Solutions.
Confrey, J., & Krupa, E. (2010). Curriculum design, development, and implementation in an era of Common Core State Standards. Arlington, VA: Center for the Study of Mathematics Curriculum.
Elam, M. E., Donham, B. L., & Soloman, S. R. (2012). An engineering summer program for underrepresented students from rural school districts. Journal of STEM Education: Innovations and Research, 13(2), 35–44.
Fisher, D., & Ivey, G. (2006). Evaluating the interventions for struggling adolescent readers. Journal of Adolescent & Adult Literacy, 50(3), 180–189.
Frederickson, N., & Cline, T. (2002). Special educational needs, inclusion and diversity: A textbook. (Chapter 12). Buckingham: Open University Press.
Frye, D., Baroody, A. J., Burchinal, M., Carver, S. M., Jordan, N. C., & McDowell, J. (2013). Teaching math to young children: A practice guide (NCEE 2014–4005). Washington, DC: National Center for Education Evaluation and Regional Assistance (NCEE), Institute of
Education Sciences, U.S. Department of Education. Retrieved from the NCEE website: http://whatworks.ed.gov
Fuchs, L., Fuchs, D., Hamlett, C., Phillips, N., Karns, K., & Dutka, S. (1997). Enhancing students’ behavior during peer-mediated instruction with conceptual mathematical explanations. The Elementary School Journal, 17(3), 223–249.
Garrison, L., & Mora, J. L. (1999). Adapting mathematics instruction for English language learners: The language concept connections. In L. Ortiz-Franco, N. G. Hernandez, & Y. De la Cruz (Eds.), Changing the Faces of Mathematics: Perspectives on Latinos (pp. 35–48). Reston, VA: National Council of Teachers of Mathematics.
Gee, J. P. (2003). What video games have to teach us about learning and literacy. New York, NY: Palgrave/Macmillan. Gersten, R. (1998). Recent advances in instructional research for students with learning disabilities: An overview. Learning Disabilities Research and Practice, 13, 162–170.
Gersten, R. (2003, March). Synthesis of intervention research on teaching mathematics to low achieving students: Implications for Title I assessment. Paper presented at the Independent Review Panel on Title One Assessment, Washington, DC.
Gersten, R., Beckmann, S., Clarke, B., Foegen, A., Marsh, L., Star, J. R., & Witzel, B. (2009). Assisting students struggling with mathematics: Response to Intervention (RtI) for elementary and middle schools (NCEE 2009–4060). Washington, DC: National Center for Education Evaluation and Regional Assistance, Institute of Education Sciences, U.S. Department of Education. Retrieved from http://ies.ed.gov/ncee/wwc/pub...
Grouws, D.W., & Cebulla, K.J. (2000). Improving student achievement in mathematics. Geneva, Switzerland: International Academy of Education.
Hall, T. (2002). Explicit instruction. National Center on Assessing the General Curriculum. Retrieved June 20, 2005, from http://www. cast.org/publications/ncac/ncac_explicit.html
Hanna, G., & Yackel, E. (2000). White paper on reasoning and proof. In M. Lindquist & G. Martin (Eds.), The future of the standards. Reston, VA: National Council of Teachers of Mathematics.
Hiebert, J., & Carpenter, T. P. (1992). Learning and teaching with understanding. In D. Grouws (Ed.), Handbook for research on mathematics teaching and learning (pp. 65-97). New York, NY: Macmillan.
Hiebert, J., Carpenter, T. P., Elizabeth, F., Fuson, K. C., Wearne, D., Murray, H., Olivier, A., & Human, P. (1997). Making sense: Teaching and learning mathematics with understanding. Portsmouth, NH: Heinemann.
Hiebert, J., & Grouws, D. (2007). The effects of classroom mathematics teaching on students’ learning. In F. Lester (Ed.), Second handbook of research on mathematics teaching and learning (pp. 371–404). Charlotte, NC: Information Age Publishing.
Hiebert, J., Morris A.K., Berk D., & Jansen, A. (2007). Preparing teachers to learn from teaching. Journal of Teacher Education, 58(1), 47–61.
Houghton Mifflin Harcourt (2015). 2015 HMH Educator Confidence Report. Boston, MA: Houghton Mifflin Harcourt.
Hyde, A. (2006). Comprehending math: Adapting reading strategies to teach mathematics K–6. Portsmouth, NH: Heinemann.
Kame’enui, E. J., Carnine, D. W., Dixon, R. C., Simmons, D. C., & Coyne, M. D. (2002). Effective teaching strategies that accommodate diverse learners (2nd ed.). Upper Saddle River, NJ: Merrill Prentice Hall.
Kamii, C. (2000). Young children reinvent arithmetic: Implications of Piaget’s theory (2nd ed.). New York, NY: Teachers College Press.
Khisty, L. L., & Chval, K. B. (2002). Pedagogic discourse and equity in mathematics education: When teachers’ talk matters. Mathematics Education Research Journal, 14(3), 4–18.
Khisty, L. L., & Morales, Jr., H. (2004). Discourse matters: Equity, access, and Latinos learning mathematics. Retrieved from http:// www.icme-organisers.dk/tsg25/s...
Lager, C. A. (2007). Types of mathematics-language reading interactions that unnecessarily hinder algebra learning and assessment. Reading Psychology, 27(2), 165–204.
Larkin, M. J. (2001). Providing support for student independence through scaffolded instruction. Teaching Exceptional Children, 34(1), 30–34.
Marzano, R. J., Gaddy, B. B., et al. (2000). What works in classroom instruction. Aurora, CO: Mid-continent Research for Education and Learning.
Marzano, R. J. (2002). Language, the language arts, and thinking. In J. Flood, D. Lapp, J. R. Squire, & J. M. Jensen (Eds.), Handbook of research on teaching the English language arts (2nd ed., pp. 687- 716). Mahwah, NJ: Lawrence Erlbaum Associates.
Math Solutions (2011). Getting started: Mathematics learning with classroom discussions. Retrieved from http://www.mathsolutions. com/documents/9781935099123_chpt1_1_14.pdf
Ministry of Education Singapore. (2006). Secondary mathematics syllabuses. Retrieved from http://www.moe.gov.sg/educatio... syllabuses/sciences/files/mathssecondary.pdf
Moschkovich, J. (2012, January). Mathematics, the Common Core and language: Recommendations for mathematics instruction for ELs aligned with the Common Core. Paper presented at the Understanding Language Conference at Stanford University, Stanford, CA.
Nason, R., Chalmers, C., & Yeh, A. (2012). Facilitating growth in prospective teachers’ knowledge: teaching geometry in primary schools. Journal of Mathematics Teacher Education, 15(3), 227-249.
National Center for Education Statistics (2015). The nation’s report card: 2015 mathematics and reading assessments. National Center for Education Statistics, Institute of Education Sciences, U.S. Washington, DC: U.S. Department of Education.
National Center on Response to Intervention. (2010). Essential components of RTI—A closer look at Response to Intervention. Washington, DC: U.S. Department of Education, Office of Special Education Programs, National Center on Response to Intervention.
National Council of Supervisors of Mathematics. (2010). Improving student achievement in mathematics by promoting positive self-beliefs. The National Council of Supervisors of Mathematics Improving Student Achievement Series. No. 7.
National Council of Supervisors of Mathematics. (2013). Improving student achievement in mathematics by using manipulatives with classroom instruction. The National Council of Supervisors of Mathematics Improving Student Achievement Series No. 11.
National Council of Teachers of Mathematics (2007). Principles and standards of school mathematics. Reston, VA: Author.
National Council of Teachers of Mathematics (2014). Principles to actions: Ensuring mathematical success for all. Reston, VA: Author.
National Joint Committee on Learning Disabilities. (2008). Adolescent literacy and older students with learning disabilities: A report from the National Joint Committee on Learning Disabilities. Retrieved from www.ldonline.org/njcld
National Mathematics Advisory Panel (2008). Foundations for success: The final report of the National Mathematics Advisory Panel. Washington, DC: U.S. Department of Education.
National Research Council. (2000). How people learn: Brain, mind, experience, and school. Washington, DC: National Academy Press.
National Research Council. (2001). Adding it up: Helping children learn mathematics. J. Kilpatrick, J. Swafford, & B. Findell (Eds.). Mathematics Learning Study Committee, Center for Education, Division of Behavioral and Social Sciences and Education. Washington, DC: National Academy Press.
Newell, A., & Rosenbloom, P. S. (1981). Mechanisms of skill acquisition and the law of practice. In J. R. Anderson (Ed.), Cognitive skills and their acquisition (pp. 1–51). Hillsdale, NJ: Erlbaum.
Pearson, P. D., & Gallagher, M. C. (1983). The instruction of reading comprehension. Contemporary Educational Psychology, 8, 317-344.
Pol, J., Volman, M., & Beishuizen, J. (2010). Scaffolding in teacher– student interaction: A decade of research. Educational Psychology Review, 22(3), 271-296.
Pressley, M. (1995). More about the development of self-regulation: Complex, long-term, and thoroughly social. Educational Psychologist, 30(4), 207-212.
Putnam, R. (2003). Commentary on four elementary math curricula. In S. Senk & D. Thompson (Eds.), Standards-oriented school mathematics curricula: What does it say about student outcomes? (pp. 161–180). Mahwah, NJ: Erlbaum.
Raiker, A. (2002). Spoken language and mathematics. Cambridge Journal of Education, 32(1), 45-60.
Raymond, E. (2000). Cognitive characteristics. Learners with mild disabilities (pp. 169–201). Needham Heights, MA: Allyn & Bacon.
Razfar, A., Khisty L.L., & Chval K. (2011). Re-mediating second language acquisition: A socioculutural perspective for language development. Mind, Culture, and Activity, 18(3), 195–215.
Reiser, R. & Dick, W. (1996). Instructional planning: A guide for teachers. Needham Heights, MA: Allyn and Bacon.
Rittle-Johnson, B., & Star, J. R. (2011). The power of comparison in learning and instruction: Learning outcomes supported by different types of comparisons. In B. Ross & J. Mestre (Ed.), Psychology of learning and motivation: Cognition in education (Vol. 55, pp. 199-226). San Diego, Elsevier.
Rose, D. (2004). The role of technology in the guided reading classroom: Apprenticeships in reading and writing. Scholastic Professional Paper. New York, NY: Scholastic, Inc.
Rose, D. H. & Meyer, A. (2000). Universal design for learning. Journal of Education Technology, 15(1), 67–70.
Rosenshine, B. (2012). Principles of Instruction: Research based strategies that all teachers should know, American Educator, 36(1).
Routman, R. (2003). Reading essentials: The specifics you need to teach reading well. Portsmouth, NH: Heineman.
Rubenstein, R. N., & Thompson, D. R. (2002). Understanding and supporting children’s mathematical vocabulary development. Teaching Children Mathematics. 107–112.
Sabean, M.P., & Bavaria, R. (2005). Sylvan Learning Center math research. Sylvan Learning, Inc.
Schoenfeld, A.H., (1988). When good teaching leads to bad results: The disasters of well-taught mathematics classes. Educational Psychologist, 23(2), 145-166.
Seeley. C. (2014). Smarter than we think: More messages about math, teaching and learning in the 21st century—A resource for teachers, leaders, policy makers and families. Boston, MA: Houghton Mifflin Harcourt.
Seidenberg, P. L. (1989). Relating text-processing research to reading and writing instruction for learning disabled students. Learning Disabilities Focus, 5(1), 4–12.
Smith, M. (2010). Best practices for next-generation assessments. Chapel Hill, NC: MetaMetrics, Inc.
Sousa, D. A., & Tomlinson, C. A. (2011). Differentiation and the brain: How neuroscience supports the learner-friendly classroom. Bloomington, IN: Solution Tree Press.
Star, J. R., Pollack, C., Durkin, K., Rittle-Johnson, B., Lynch, K., Newton, K., & Gogolen, C. (2015). Learning from comparison in algebra. Contemporary Educational Psychology, 40, 41-54.
Stecker, P., Fuchs, L., & Fuchs, D. (2005). Using curriculum-based measurement to improve student achievement: Review of research. Psychology in the Schools, 42(8), 795–819.
Stein, M. K., Smith, M. S., Henningsen, M. A., & Silver, E. A. (2000). Implementing standards-based mathematics instruction: A casebook for professional development. New York, NY: Teachers College Press.
Stylianou, D. A., & Silver E. A. (2004). The role of visual representations in advanced mathematical problem solving: An examination of expert-novice similarities and differences. Mathematical Thinking and Learning, 6(4), 353–87.
Swan, K. (2002). Building learning communities in online courses: the importance of interaction. Education, Communication & Information, 2(1), 23-49.
Thompson, D. R., & Rubenstein, R. N. (2000). Learning mathematics vocabulary: Potential pitfalls and instructional strategies. Mathematics Teacher, 7(93), 568–574.
Torgesen, J. K. (2002). Lessons learned from intervention research in reading: A way to go before we rest. In R. Stainthorpe (Ed.), Learning and teaching reading (pp. 89–103). British Journal of Educational Psychology Monograph. London: British Psychological Society.
Van de Walle, J. A., Karp, K. S., & Bay-Williams, J. M. (2010). Elementary and middle school mathematics: Teaching developmentally (7th ed.). New York, NY: Pearson Education, Inc.
Vaughn, S., & Denton, C. (2008). Tier 2: The role of intervention. In D. Fuchs, L. Fuchs, & S. Vaughn. (Eds.), WIS prevention—response to intervention: A framework for reading educators (pp. 51–69). Newark, DE: International Reading Association.
Visnovska, J., & Cobb, P. (2015). Learning about whole-class scaffolding from a teacher professional development study. ZDM Mathematics Education, 47(7).
Wiggins, G. (2012). Seven keys to effective feedback. Educational Leadership, 70(1), 10-16.
Williams, L. (2008). Tiering and scaffolding: Two strategies for providing access to important mathematics. Teaching Children Mathematics, 14(6), 324–330.
Witzel, B. S., Mercer, C. D., & Miller, M. D. (2003). Teaching algebra to students with learning difficulties: An investigation of an explicit instruction model. Learning Disabilities Research & Practice, 18(2), 121–131.
Wong, K. (2004, July). Using multi-modal think-board to teach mathematics. A presentation for TSG 14: Innovative approaches to the teacher of mathematics, ICME-10, DTU: Technical University of Denmark, Copenhagen, Denmark.
Zielezinski, M. B., & Darling-Hammond, L. (2016). Promising practices: A literature review of technology use by underserved students. Stanford, CA: Stanford Center for Opportunity Policy in Education.








