There are many ways to think fundamentally about the concept of mathematics. One way is to separate the subject into how to write math (oftentimes, algebra) and how to draw it (oftentimes, geometry). A coordinate plane graph lives in the space between writing and drawing mathematics, as the graph can often be described both by written equations and visual shapes.
In the U.S., students in Grades 5 and up typically first learn to perform x- and y-axis graphing on a coordinate plane. Once they are ready for positive and negative integers, often by Grade 6, you can extend graphing to all four quadrants of the coordinate plane.
- Key Standard: Graph points in all four quadrants of the coordinate plane. (Common Core 6.NS.C.8, Florida BEST MA.6.GR.1.1)
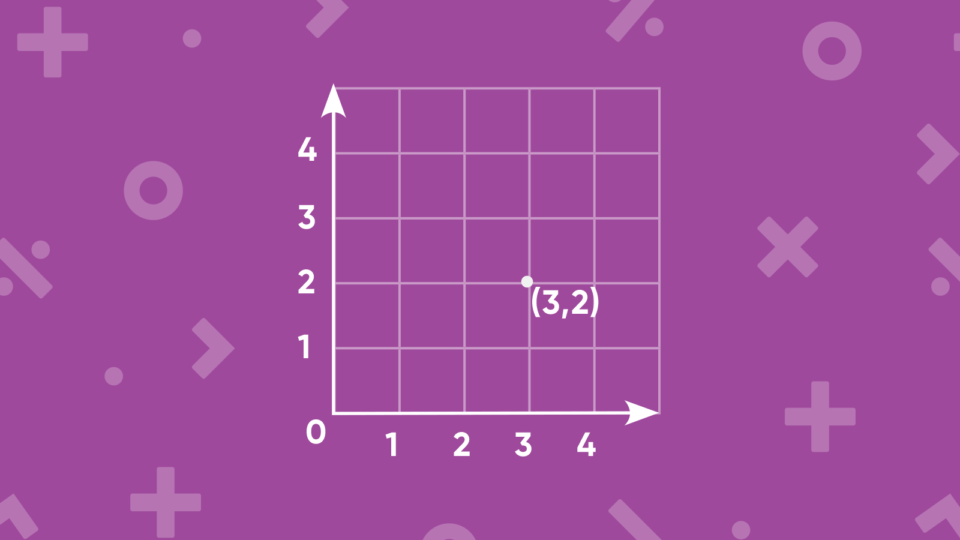
Points on a Grid
A location, or point, on a grid can be identified by an ordered pair such as (3,2), which names the coordinates of that point. The first number tells how far to the right or left the point is located in the horizontal direction. The second number tells how far up or down the point is located in the vertical direction. Note that the point (3,2) is not the same as point (2,3). The numbers in an ordered pair are called coordinates.
Integers
The most common numbers that we encounter—in everything from speed limits to serial numbers—are natural numbers. These are the counting numbers that start with 1, 2, and 3, and go on forever. If we start counting from 0 instead, the set of numbers are instead called whole numbers. The integer numbers (or simply integers) extend whole numbers to their opposites: ...–3, –2, –1, 0, 1, 2, 3.... Notice that 0 is the only number whose opposite is itself.
Historically, negative numbers largely came about as a way of solving equations that otherwise wouldn't have solutions, such as x + 8 = 3. However, humans have long had some conception of negative numbers, due to phenomena such as measuring sea level or debt. Notice how mathematics rarely presents just one model for the real world. There is nothing stopping you from representing a $5 debt by representing "$5" using red text instead of black or adding the word "owed" next to it.
Representing the concept of being opposite using a negative sign lets us represent all the integers on a number line that extends both to the left and to the right of zero. The positive integers are represented to the right of 0 and the negative integers are represented to the left of 0. Note how numbers such as −3 and +3 are opposite numbers.
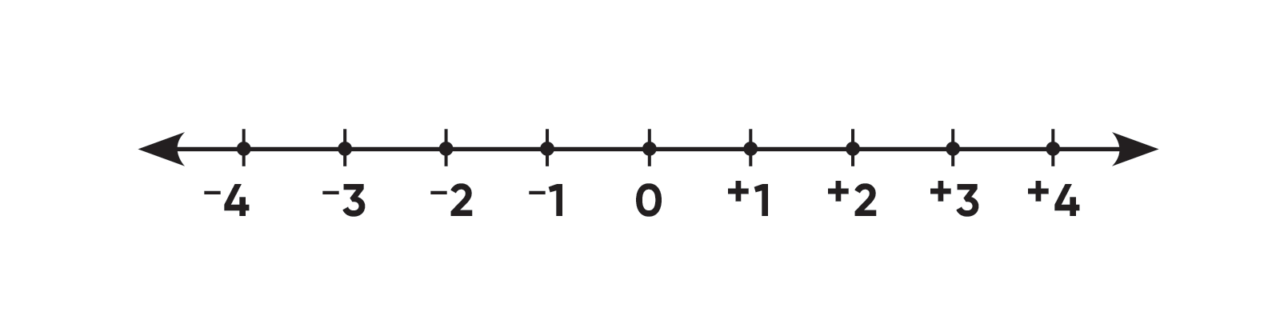
Coordinate Plane
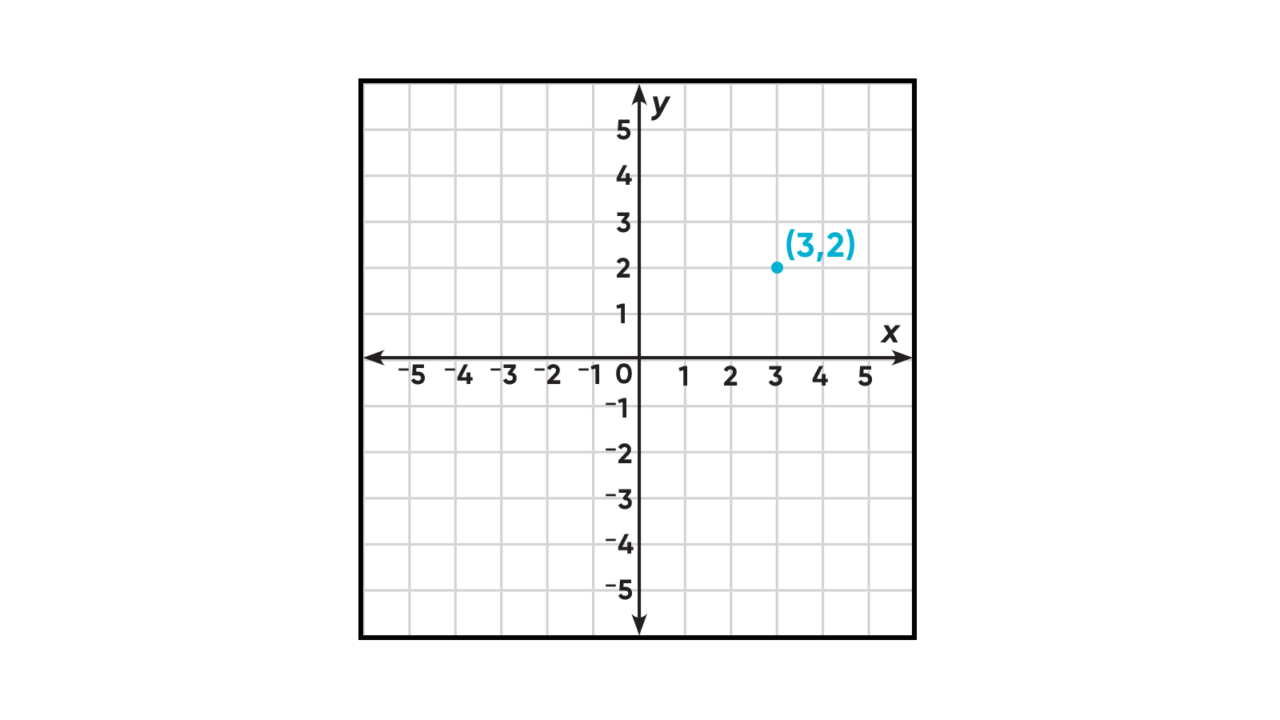
Coordinate graphing is a visual method for showing relationships between numbers. The relationships are shown on a coordinate plane. A coordinate plane has two perpendicular lines, or axes (pronounced AK-seez), labeled just like number lines. With the extension of the number system to include negative numbers, each axis can be extended in two directions. The horizontal axis is usually called the x-axis. The vertical axis is usually called the y-axis. The point where the x- and y-axis intersect is called the origin.
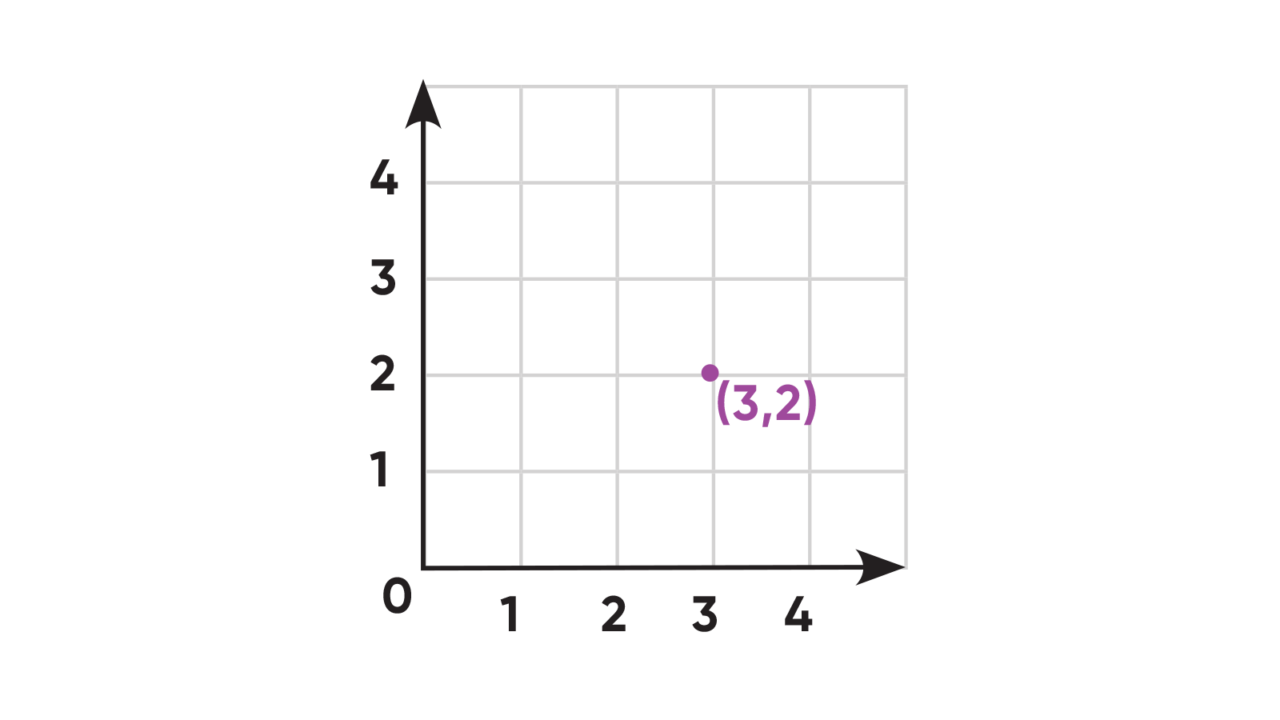
The numbers on a coordinate plane are used to locate points. Each point can be identified by an ordered pair of numbers; that is, a number on the x-axis called an x-coordinate, and a number on the y-axis called a y-coordinate. Ordered pairs are written in parentheses (x-coordinate, y-coordinate). The origin is located at (0,0). Note that coordinates are often written with no space after the comma.
The location of (3,2) is shown on the coordinate plane below. The x-coordinate is 3. The y-coordinate is 2. To locate (3,2), move 3 units to the right on the x-axis and 2 units up on the y-axis.
What Are the Quadrants on a Graph?
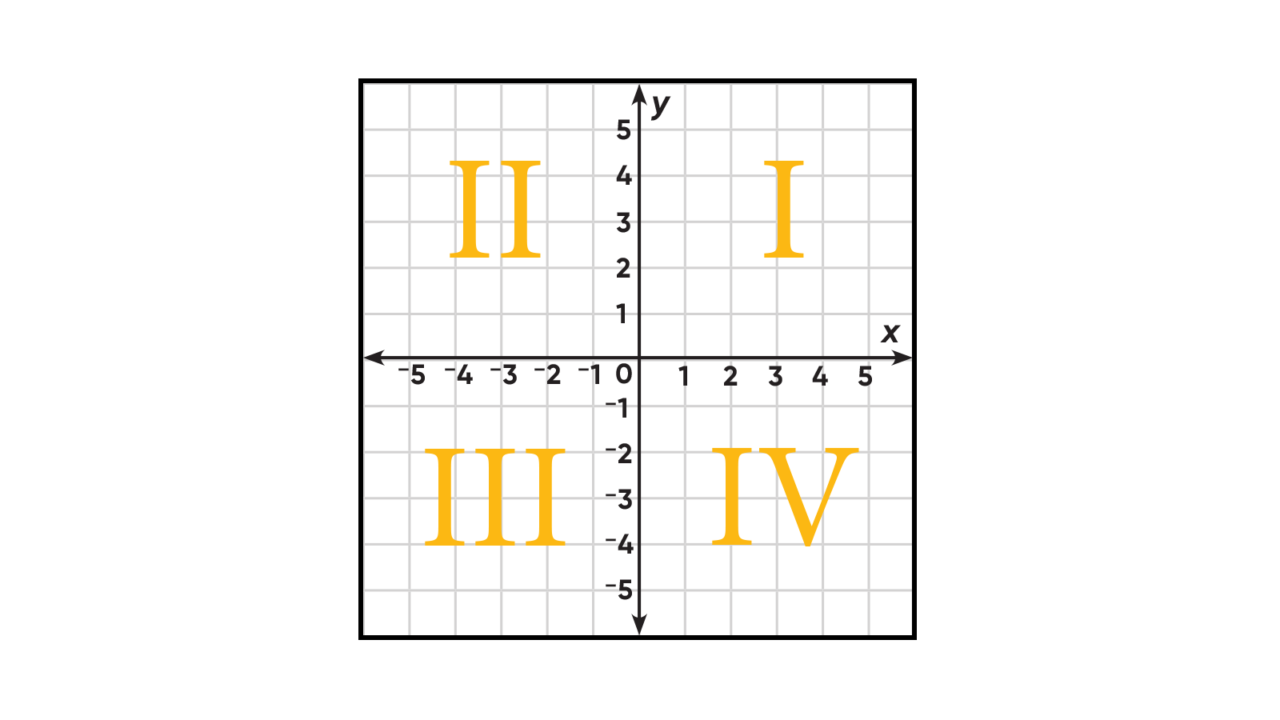
The coordinate axes divide the plane into four regions called quadrants (or sometimes grid quadrants or Cartesian coordinate quadrants). Students often ask, how are quadrants numbered? A common heuristic is to think of the numbering happening in the same order that we write the letter C. Coordinate plane quadrants are numbered I, II, III, and IV as shown on the grid below.
In Grade 5, students do not usually need to know the numbering system, but should recognize that the appropriate quadrants for ordered pairs can be identified according to the signs of the numbers.
- All points in Quadrant I have two positive coordinates.
- All points in Quadrant II have a negative x-coordinate and a positive y-coordinate.
- All points in Quadrant III have two negative coordinates.
- All points in Quadrant IV have a positive x-coordinate and a negative y-coordinate.
There are many opportunities for discourse that focus on all quadrants of the coordinate plane. Have students brainstorm how someone making an animation or video game might use it, for example. Or show students a variety of graphs taken from different activities and books and have them share what they notice and wonder.
A coordinate plane lets you both visualize and calculate the length of a line segment. Although students do not learn to calculate the length of slanted line segments until learning the Pythagorean Theorem (typically in Grade 8), a four-quadrant plane is enough to find the length of horizontal or vertical line segments.
For horizontal line segments, the length is the difference between the x-coordinates of the endpoints. For vertical line segments, the length is the difference between the y-coordinates of the endpoints.
Functions
Around Grade 5, functions are graphed from tables of given values. All values are positive, thus the graphs of functions studied in this chapter are in Quadrant I only. Formal definitions and extended work with functions are usually not taught until at least Grade 8.
A function is a rule that associates one and only one value of one variable with each value of another variable. For example, the function y = 2x expresses y in terms of x. For each value of x, there is one and only one value of y:
- If x is 3, then y is 6.
- If x is –40, then y is –80.
- If x is 0, then y is 0.
If an equation includes x and y and has the property that for each x, the equation can be solved to give exactly one value of y, then the equation is a function. An equation that can be written Ax + By = C, where A, B, and C are fixed numbers, is a linear equation.
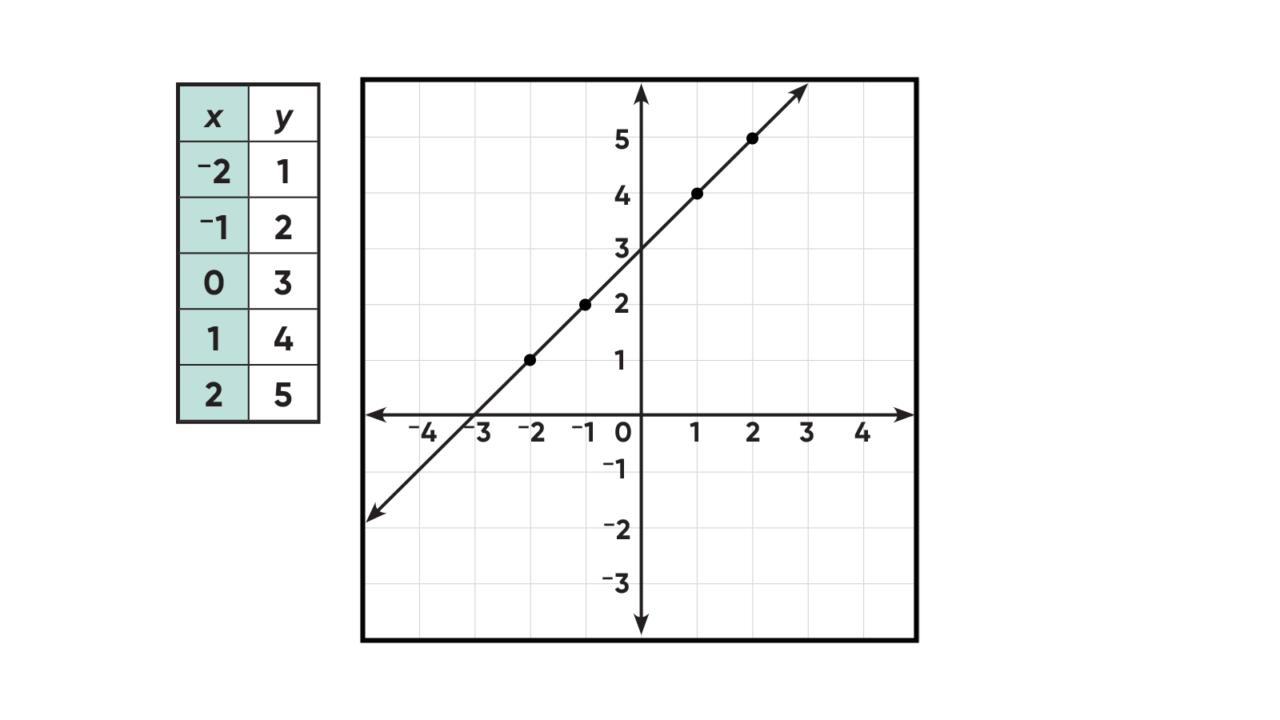
The graph of a linear equation is a straight line. One way to see this is to create a table of values for x and y, and then interpret each row of the table as the x- and y-coordinates of points in the coordinate plane. When you connect the points, you get a line.
See, for example, the graph of y = x + 3. Graphing the points in the table shown means placing a dot at the points (–2,1), (–1,2), (0,3), (1,4), and (2,5). Then connect the points with a straight line.
***
Unlock quadrant numbers on a graph and more for students who struggle with mathematics with Math 180, our revolutionary approach to math intervention for Grades 5–12.












