Number theory—the study of integer numbers—has fascinated mathematicians for years. Fundamental to number theory are whole numbers: 0, 1, 2, 3, and so on. The basic building blocks for all whole numbers are prime numbers. A prime number is a whole number that has only two factors: itself and one. When a number has more than two factors, it is said to be a composite number.
The numbers one and zero are unusual cases. The number one has only one factor and is considered to be neither prime nor composite. The number zero has an infinite number of factors, as zero can be divided evenly by anything except zero. For this reason, zero is also considered neither prime nor composite.
Check Your Understanding:
- Is 36 a prime number or composite number? (Composite, because it has many factors other than 1 and 36: 2, 3, 4, 6, 9, 12, and 18.)
- What are all of the prime numbers less than 10? (2, 3, 5, and 7.)
Prime Factorization of 36
Students in Grades 4 and up are typically ready to learn about prime factors, and students in Grades 6 and up are typically ready to investigate the prime factorization of a number and explore how it can be used to generate all whole numbers.
Key Standards:
- Find factor pairs and recognize that a whole number is a multiple of each of its factors.
- Write and evaluate numerical expressions that represent prime factorizations and involve whole-number exponents.
When a composite number is written as a product of all of its prime factors, we have the prime factorization of the number. Thus, if we write 36 as a product of all of its prime factors, we can find the prime factorization of 36.
We can write 36 as a product of prime factors: 36 = 2² × 3². The expression 2² × 3² is said to be the prime factorization of 36.
The Fundamental Theorem of Arithmetic
The Fundamental Theorem of Arithmetic states that every whole number can be factored uniquely (except for the order of the factors) into a product of prime factors. For example, there are many whole numbers that can divide 36: 2, 3, 4, 6, 9, 12, and 18. But no matter which factor you start with, when the number 36 is factored completely, it will always look like 2² × 3². The order in which you factor 36 doesn't matter. Examine the two factor trees of 36 given below.
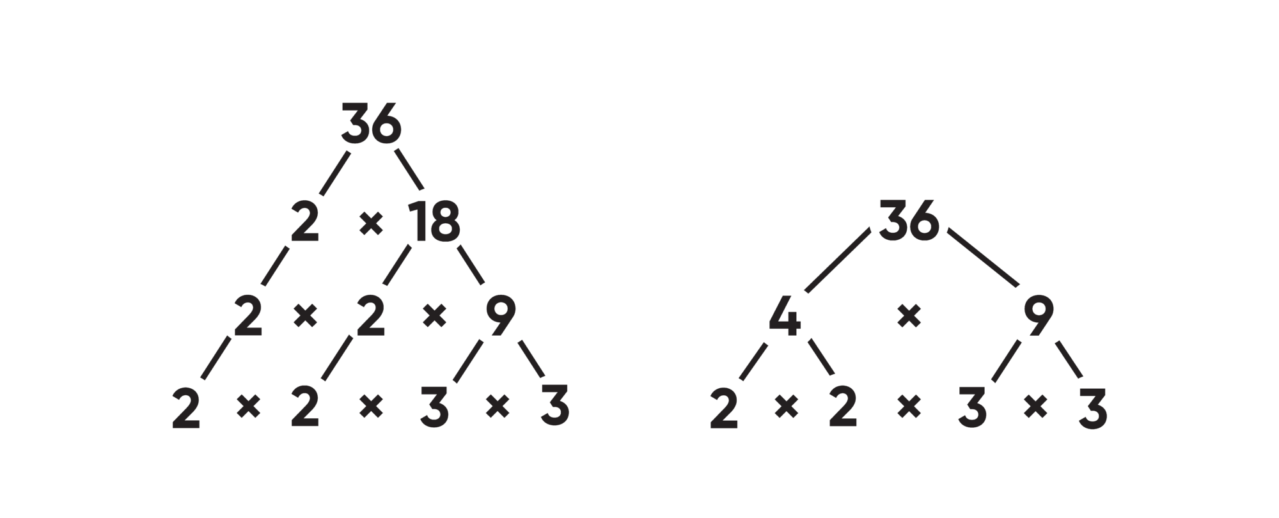
In the end, it didn't matter if we started factoring 36 using 2 × 18 or 4 × 9. In the end, we still have two factors of 2 and two factors of 3, or altogether, 2² × 3². This would be true if we had started to factor 36 as 12 times 3 or 6 times 6 instead.
Knowing the rules for divisibility will be very helpful when seeking to write a number in prime factorization form. A rule for checking if a number is divisible by two is by seeing if it ends in 0, 2, 4, 6, or 8. Notice that two is the only even prime number.
Dividing by Prime Numbers
Another way to factor a number other than using factor trees is to start dividing by prime numbers, as shown below.
Using this method, the prime factorization is found by looking at all of the numbers outside the division symbols. Once again, we can see that 36 = 2² × 3². Notice the key importance of exponents in writing the prime factorization of a number. An exponent tells how many times the base is used as a factor. In the prime factorization of 36 = 2² × 3², both of the factors 2 and 3 have an exponent of two because each factor appears twice.
It is notoriously difficult to determine whether a number is prime, especially when the number is very large. One useful strategy to check whether a number is prime or not is to only try dividing by prime numbers that, when squared, remain less than the original number. For example, to see if 131 is prime, you need only check for divisibility by 2, 3, 5, 7, and 11, since 13² = 169, and 169 is greater than 131. This strategy works because if 131 were divisible by a prime number greater than 13, then the other factor would have to be less than 13 and you would have already checked it.
***
Looking for comprehensive math instruction for questions beyond "What is the prime factorization of 36?" Explore HMH Into Math, our core math solution for Grades K–8.
